軌跡(二):媒介変数消去型
<この記事の内容>:前回「軌跡(1):0から2問で軌跡の基本を理解する!」に引き続いて、今回は「パラメーター」を消去する形の軌跡の求め方、考え方を解説していきます。
<この分野の復習>:→「”図形と方程式”の解法・解説記事の総まとめ」
目次(タップした所へ飛びます)
媒介変数(パラメーター)とは?
媒介その名前が示すように『2つ(やそれ以上)』の変数を”媒介(関連づける)文字”で、それが”変数(一定の数ではない)”であるとき、その文字を『媒介変数』や『パラメーター』と言います。
・・・ただこれだけでは??となる人が多いと思うので、実際に問題を通して学んでいきましょう。
基礎問題1(定義域に制限がないパターン)
いま、全ての実数を満たす変数”t”を使って、x、yが次のように示されている。この条件を満たす軌跡はどのようなものか。また、その軌跡の方程式を書け。
\(x=2t+1\)
\(y=4t^{2}+2t+3\)
解答解説1
このように、x=(tの式),y=(tの式)のようにxとyがそれぞれ(tの式)で表されている時の”t”のことを媒介変数と言います。(もちろん、媒介変数の文字は”t”である必要はなく、他の文字でも構いません)
イメージとしては、「tが『xとyの各変数』の間を取り持っている」といった感じです。
では、本題に進みましょう。
tが実数全体で、xとyが連立されていたので、このような場合は”パラメーターを消去する”という解法が鉄則です。
具体的には、以下のようにstep1→step2→step3の順に進めます。
step1:まずx=(tの式)をt=(xの式)に式変形
\(x=2t+1\)だから、⇔\(2t=x-1\)⇔\(t=\frac{x-1}{2}\)
したがって、t=(xの式)と変形できました。
step2:もう一方のy=(tの式)のtに先ほどのt=(xの式)を代入
次に、\(y=4t^{2}+2t+3\)の式中のパラメーター”t”にstep1で求めたxの式を代入します。
\(t=\frac{x-1}{2}\)より、
$$y=4\times (\frac{x-1}{2})^{2}+2\times \frac{x-1}{2}+3$$
これを計算して整理すると、
step3:軌跡の方程式が求まる
\(y=x^{2}-x+3\)さらに平方完成して、
$$y=(x-\frac{1}{2})^{2}+\frac{11}{4}$$となって
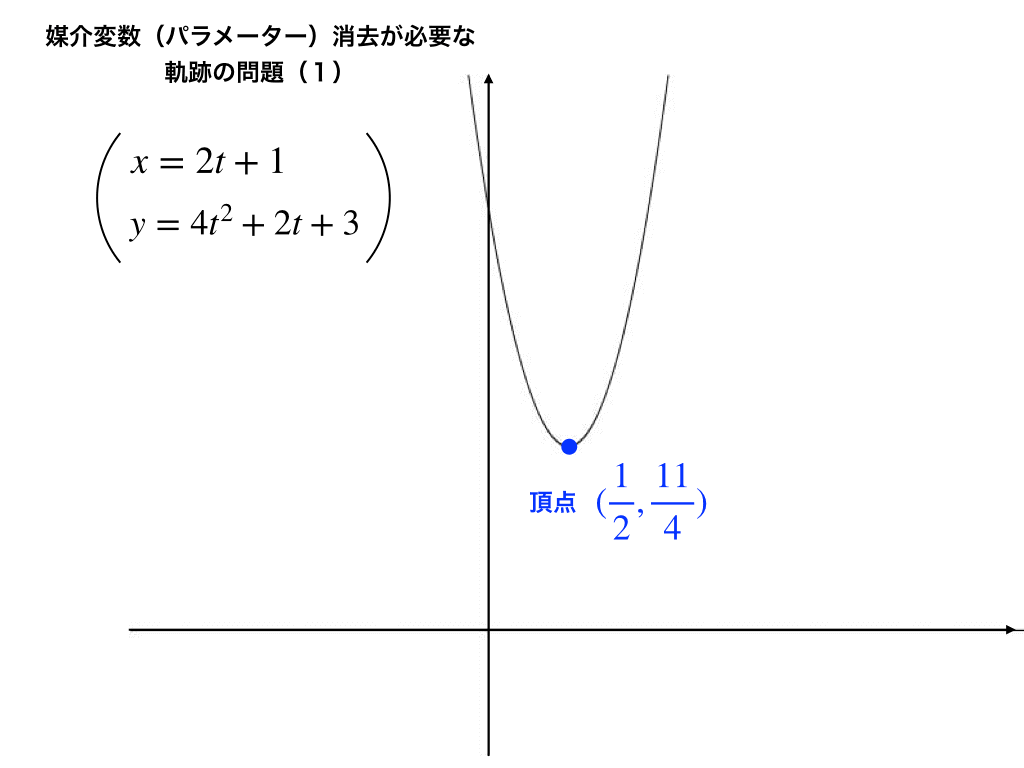
上のグラフのように、頂点\(\left(\frac{1}{2},\frac{11}{4}\right)\)の下に凸な放物線が例題1の軌跡となります。・・・(答)
隠れた条件と媒介変数
ここでは、先ほどの例題1を『ほんの少しだけ』変化させた(しかし非常に重要な)問題を通して『よくやりがちなミス』と、正しい解法を紹介します。
重要問題2
次の軌跡の方程式を求めて、どのような軌跡を描くか図示せよ。(ただし、tは実数とする)
\(x=t^{2}+2\)
\(y=t^{4}+3t^{2}+2\)
一見すると、例題1と何も変わらないように見えますが・・・
解答と注意するポイント
例1同様に、
\(x=t^{2}+2\)だから、⇔\(t^{2}=x-2・・・(※)\)
したがって、t=(xの式)と変形できました。
(注!:ここで『ある事』をしないとバツになってしまうのですが、とりあえず進めて見ましょう。)
\(y=t^{4}+3t^{2}+2\)は『\(t^{2}\)』を代入できるので、(※)をy=に代入すると、
$$(x-2)^{2}+3(x-2)+2=x^{2}-x$$
よって、下の図のような頂点\(\left(\frac{1}{2},\frac{-1}{4}\right)\)の下に凸な放物線。←誤り
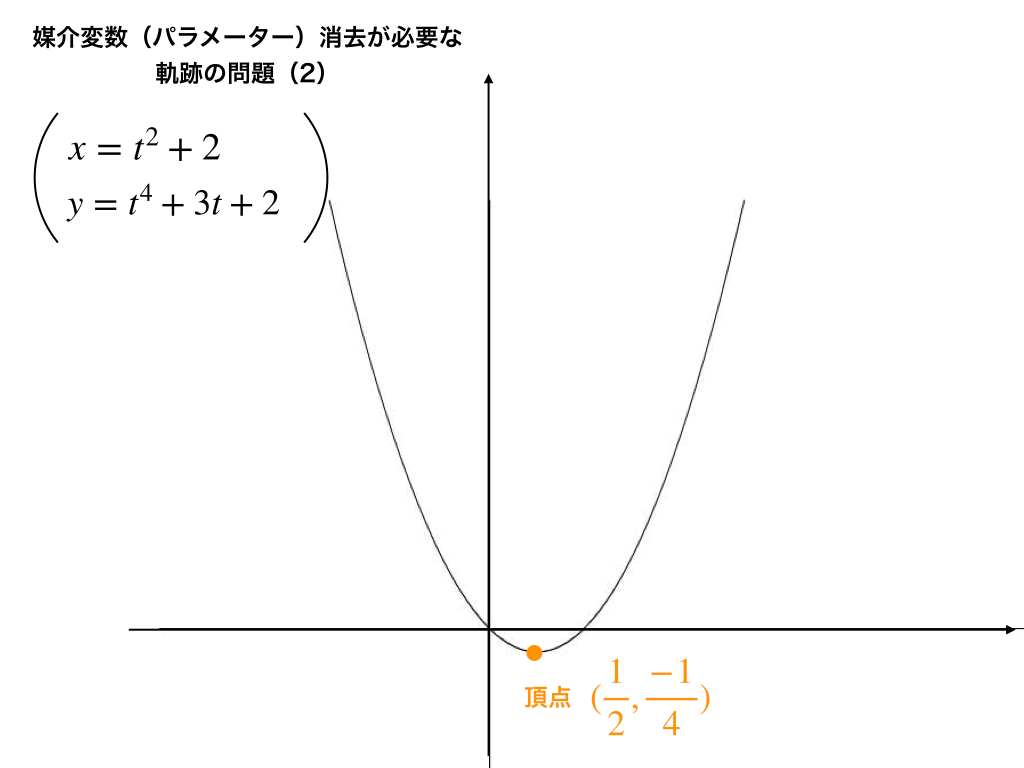
<これではバツになってしまう>
どこが問題だったのでしょうか?
(注!)のところで『ある事』をしないといけないと書きました。
それは、『tが実数』⇔『(実数の二乗は正)』より、
・【隠れていた条件】\(0≦t^{2}=x-2・・・(※)\)
すなわち\(0≦x-2 ⇔2≦x\)という「定義域の制限」を見落としていたのです。
このように、文字の代入などを行う際には『何か隠れた条件がないか?』と言う細心の注意を持っておくことが大切です。
正答(定義域の制限を加える)
上の制限を加味して、$$y=(x-\frac{1}{2})^{2}-\frac{1}{4} の2≦xの部分$$・・・(答)
図示すると、下のグラフのように赤の太線部分がこの問題の答えとなる軌跡です。
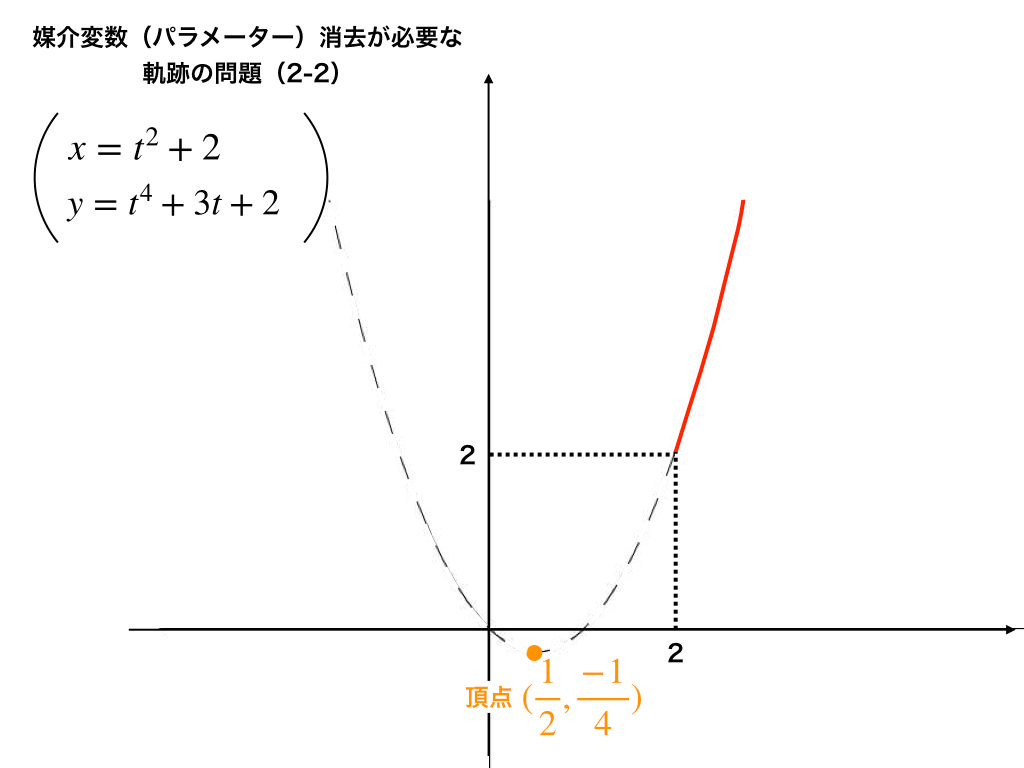
<正しい軌跡(赤色太線部分)>
まとめと関係する記事・続編へ
・パラメータを消去するパターンでは、「隠れた条件」に注意する。
・次回は、今回の例題より少し難易度を上げた問題(入試頻出レベル)の演習をしていきます。
〜「(数学Ⅲ)媒介変数で表示された曲線の描き方・面積の求め方」〜
関連記事
〜軌跡と領域〜
第1回:「軌跡を0から学ぶ!条件を満たす点とその集合」
第2回:「(今ここです)」
第3回:「(作成中)」
〜領域〜
第1回:「領域の基礎と様々な例」
第2回:「領域を用いて式の最大値・最小値を求める方法(線形計画法)」
今回も最後までご覧いただき、ありがとうございました。
当サイト:「スマナビング!」では、読者の皆様からのご意見・ご感想の募集をコメント欄で行なっています。
また、お役に立ちましたら、B!やシェアをしていただけると、とても励みになります。
・お問い合わせ/ご依頼/その他のご連絡は、記事上部の【運営元ページ】よりお待ちしております。

