【熱力学第一法則】と色々な式を整理
(熱力学シリーズ:第一回)
<この記事の内容>:熱力学の基礎中の基礎である
・【第一法則】「\(Q_{IN}=\Delta U+W_{OUT}\)」の式から、
・何種類もあって複雑な《内部エネルギー・仕事・熱量》の計算公式までまとめ、
・確認問題を通してそれらの使い方を解説していきます。
目次(タップした所へ飛びます)
熱力学第一法則とは
すぐ下にある式1のことを《熱力学の第一法則》といいます。
第一法則の式とQ・ΔU・W
\(Q_{IN}=\Delta U+W_{OUT}\)・・・式1
つまり、「気体に《与えられた熱量》は、(内部)エネルギーの変化量と《外部へ『した』仕事》の和と等しい」という事を言っています。
“添え字”について
(※:添え字の部分をどう書くかは人によって異なり、“外部から入って来る”時「in」「外から」など、“外部へ出て行く”ときは「out」「外へ」など様々です。
が、自分の使いやすいものを選んで使う様にしましょう。
添え字が無いor間違えると、符号が逆になったりして計算ミスなどの原因になります。)
ではこれから、\(Q_{in},\Delta U ,W_{外へ}\)のそれぞれに付いて説明していきます。
Q:熱量の意味と式
Q(J)は単位でもわかるように”熱量”で、外部から熱を与えられると\(Q_{in}\)、熱を放出すると\(Q_{out}\)という風に書きます。
Qを計算する前に知っておく必要がある、CvとCpに付いて先に見ていきます。
定積・定圧モル比熱とは
Cv:添字の"v"は定積の積=体積(=Volume)の”v”です。「状態変化と”比熱”・”熱容量”(熱化学・熱力学)」でも解説している比熱の”mol版”といえます。
【体積一定】のもとで、n(mol)の気体をΔT(K)だけ上昇させるために必要な【熱量Q(J)】を求めるときに使用し、単位は\(\frac{J}{mol\cdot K}\)です。
Cp:同様に、添字の"p"は定圧の圧=圧力(=pressure)の”P”です。
【圧力一定】のもとで、n(mol)の気体をΔT(K)だけ上昇させるために必要なQ(J)を求めるときに使用します。単位はCvと同じです。
また、【単原子分子からなる理想気体】のときのみ、
\(C_{V}=\frac{3}{2}R,C_{P}=\frac{5}{2}R\)となります。(導出は今後の記事で行います)
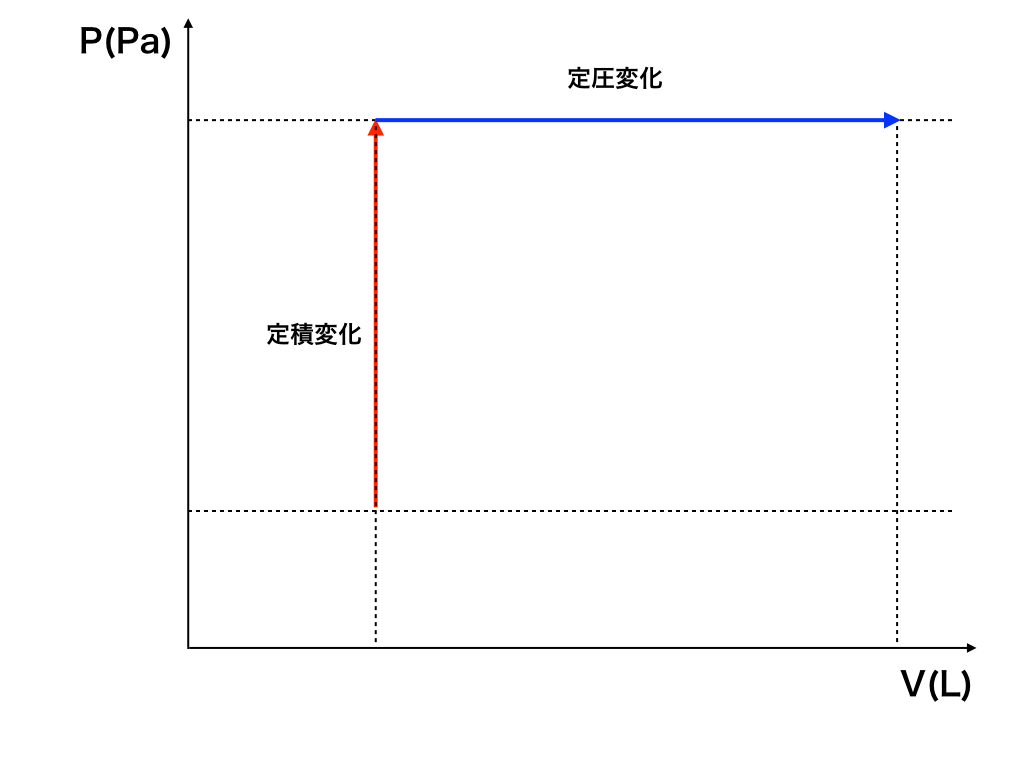
“定積”変化の時の式
(図の赤色矢印のように、体積不変=一定のままの状態変化)
\(Q_{in}=n\cdot Cv\cdot \Delta T\)
“定圧”変化の場合の式
(図の青色矢印のように、圧力不変=一定のままの状態変化)
\(Q_{in}=n\cdot Cp\cdot \Delta T\)
ΔU:内部エネルギーの変化量の意味と式
ΔUのΔは、(デルタ=変化)を意味し、Uの意味はその気体の『内部エネルギー』です。
従ってΔUは、気体の内部エネルギーが”どれだけ変化したか?”という変化量を文字でおいたものです。
\(\Delta U=n\cdot Cv\cdot \Delta T\)
内部エネルギーは個々の原子の運動エネルギーの総和。
(詳しくは「(作成中です)気体分子運動論」で解説します)が、理想気体のΔUは温度Tの変化だけに影響を受けます。
(※重要:圧力や体積の変化の影響は受けません)
そして、これまで比熱をcや、熱容量をCと置いていた様に、計算には《モル比熱Cv》を使います。
定積変化の時:
(第一法則)Q=ΔU+Wより、体積が変化しないのでW=0となります。すなわちQ=ΔU
nCvΔT=ΔUです。・・・(式2)
定圧変化のとき:
当然圧力は一定ですが、その体積は一定ではありません。
体積が変化する分だけ“Wも変化”するため、Qはより大きい値になる必要があります。
一方ΔUは(式2と、「圧力や体積によらない+温度変化のみに影響される」)ので、
【n・Cv・ΔT】のままの式で求めることができます。
(ここが『どのような変化でも、ΔUの計算には”定積モル比熱”Cvを使う』という悩む人が多いポイントです。
【定圧】や【定積】と言う名前から、始めは混乱しがちですが、次第に分かってくるので取り敢えずΔU=n・Cv・ΔTを頭に入れておいてください。)
W:気体のした仕事の意味と式
さて、定積変化では上述した通り体積変化がない=仕事0ですが、それ以外の定圧などの場合は仕事Wが発生します。
\(W_{外部へ}=P\cdot \Delta V\)

これまでの式を上でまとめました。次の問題編へ行く前にもう一度確認しておきましょう。
定着問題と第一法則の使い方
ではここまでの知識を整理しつつ、どのような問題が出題され、解くのかを見ていきましょう。
問題
定着問題:いま、1(mol)の"単原子分子"から構成される、理想気体の圧力や体積を<図1>の様に変化させる。
状態X:\(P_{1},V_{1}\)の時の温度は\(T_{1}\)である時、以下の問いに答えよ。
状態Yでの
・温度\(T_{Y}\)を\(T_{1}\)を用いて表せ。
・X→Yでの\(\Delta U_{X\rightarrow Y}\)
状態Zでの
・温度\(T_{Z}\)と
・Y→Zでの気体の【した】仕事\(W_{Y\rightarrow Z}\)
・Y→Zでの\(Q_{in(Y\rightarrow Z)}\)
をそれぞれ求めよ。
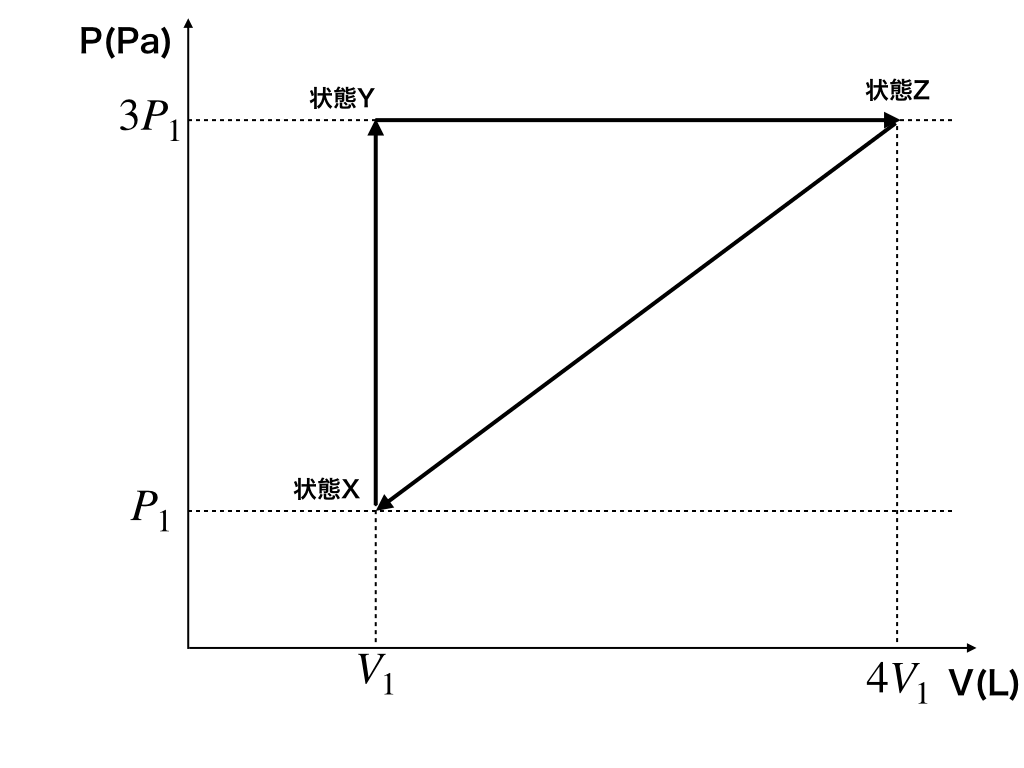
<図1>
解答と解説
まずは、各状態でのTを「状態方程式」から出しておきます。(参照:「理想気体の状態方程式」)
\(3P_{1}\cdot V_{1}=1\cdot R \cdot T_{Y}\)
\(3P_{1}\cdot 4V_{1}=1\cdot R \cdot T_{Z}\)
ここで、
\(P_{1}\cdot V_{1}=1\cdot R \cdot T_{1}\)
と比べて、\(T_{Y}= 3T_{1};T_{Z}= 12T_{1}\)
つぎに、X→Yは「定積」変化で、内部エネルギーの変化量は
\(\Delta U_{X→Y}=1\cdot Cv\cdot \Delta T\)
$$\Delta T=3T_{1}-T_{1},C_{V}=\frac{3R}{2}$$より、\(\Delta U_{X→Y}=3RT_{1}=3P_{1}V_{1}\)
次にY→Z間の\(W_{OUT}=3P_{1}\cdot (4-1)V_{1}\)
よって、\(W_{OUT}=9P_{1}V_{1}\)
最後にY→Zは定圧、かつ、\(P_{1}V_{1}=RT_{1}\)より、
$$Q_{in(Y→Z)}=\frac{5R}{2}\cdot 9T_{1}=\frac{45R}{2}T_{1}$$
よって、$$Q_{in(Y→Z)}=\frac{45}{2}P_{1}V_{1}$$
熱力学(一)まとめと関連記事
今回はたくさんの式や新しい概念が登場して、大変だったと思います。
ぜひ何度も見直して、次回以降の(もう少し式が増えます・・・)準備をしておきましょう!
次回:”ポアソンの式“とその使い方
シリーズ第一回:「(今ここです)\(Q_{in}=W_{外}+\Delta U\)熱力学の基本と第一法則」
シリーズ第二回:「ポアソンの式(法則)の導出と断熱変化」
シリーズ第三回:「予定:熱力学”第二”法則と永久機関・熱効率etc,,,」
今回も最後までご覧いただきまして、ありがとうございました。
【受験/学習メディア】:「スマホで学ぶサイト、スマナビング!」では,読者の皆さんのご感想を募集しています。コメント欄迄ぜひお寄せください。
(※:ただいま、個々の問題の質問などには対応出来ない場合がございます。)
・その他のお問い合わせ/ご依頼/タイアップなどに付きましては、引き続き、ページ上部の【運営元ページ】よりご連絡をお願い致します。

