正規直交基底とその計算方法(グラム・シュミットの直交化法)
<前回の復習とこの記事の内容>:前回の「計量線形空間の定義とコーシー=シュワルツの不等式」では内積の定義、そして内積空間(計量線形空間)、さらに応用として有名不等式の証明まで行いました。
この記事では内積の重要性を踏まえたところで、線形代数では欠かすことのできない「正規直交基底」と、それを作り出す『グラム・シュミットの直交化法』について解説していきます。
目次(タップした所へ飛びます)
正規直交基底とは
正規直交基底と言う用語は、三つの用語「正規」「直交」「基底」に分解することが出来ます。それぞれの定義をここで紹介していきます。
『正規直交基底』というとなんとなく難しそうな印象を受けますが、次の項で『基底』についてしっかりと復習してから分解した一つ一つの意味を学ぶ事で、実際は恐るるに足らずだということがわかってもらえるかと思います。
基底のおさらい
『基底』とは、線形(ベクトル)空間における元の組みで、8個の定義を満たしたものでした。
(参考→「基底と標準基底の意味と定義」)
<基底のイメージ>:2次元の線形空間での基底のイメージとしては、(1,0),(0,1)のベクトルを思い浮かべてもらうと良いです。
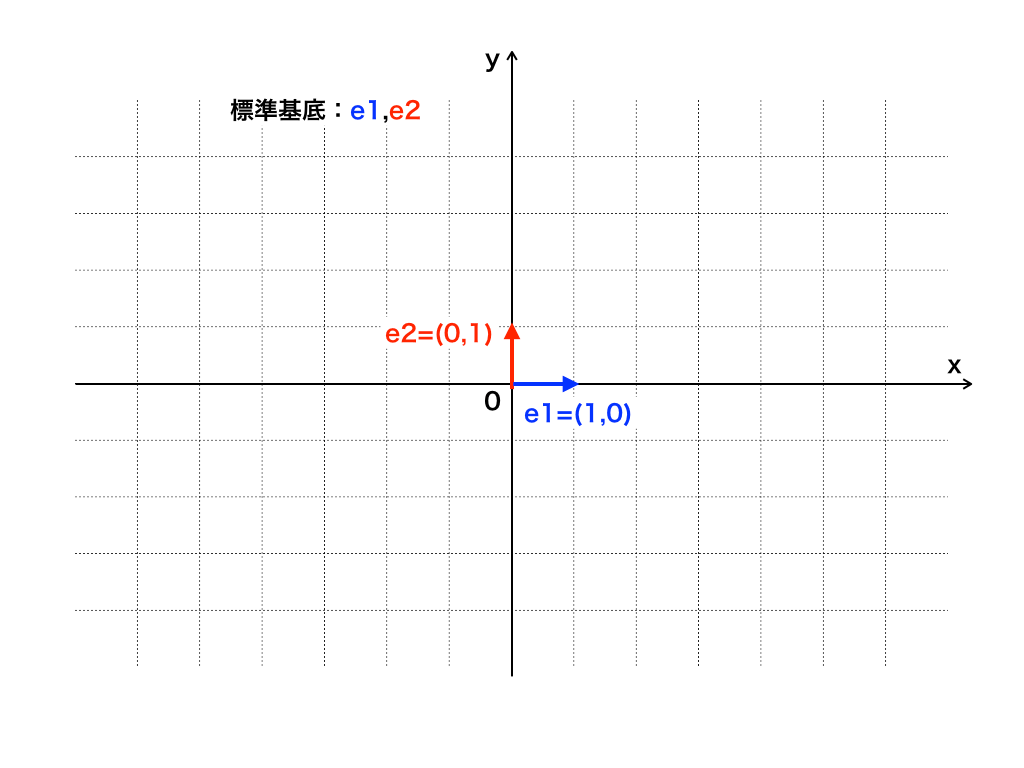
上の2つのベクトルで、線形空間上のあらゆるベクトルを表すことができます。
正規直交基底の特徴と条件
さて、ここからが本題です。
まず、”直交基底”の意味は、計量ベクトル空間における基底が、”ある条件”を満たしている必要があります。
それは、基底の組の内積を計算すると”0”になる、というものです。
内積が0ということは、互いの元が垂直である=直交していると言えるので、「直交基底」という名がついているのです。
次に直交基底の前に付いている”正規”の言葉の意味です。
正規とは
「正規である」とは「ノルムが1に等しい」ということです。3次元空間上のベクトル(1,0,0)などは長さ、ノルムが1であり正規であると言えます。
正規直交基底の具体例
つまり、この三つの性質「正規」・「直交」・「基底」を満たすベクトルたちが、「正規直交基底」というものになるということです。
以降この記事では一般的な正規直交基底の成分をe1,e2,…,enと表すことにします。
ではもう少し具体的に正規直交基底の例を考えてみます。
もっとも簡単なものは、先ほど図で紹介した\((1,0),(0,1)\)や、\((1,0,0),(0,1,0),(0,0,1)\)が挙げられ、これは三次元空間\(R^{3}\)の正規直交基底です。
\((\cos\theta,-\sin\theta),(\sin\theta,\cos\theta)\)も実は\(R^{2}\)の正規直交基底で、(1,0),(0,1)をθだけ回転させたものになります。このように、様々な種類の例を挙げることができます。
この正規直交基底があれば、様々なベクトルを上手く表すことが出来るのです。
シュミットの直交化法の意味と計算方法
上で紹介したように、『正規直交基底』は線形代数においては非常に便利であり、欠かすことのできない存在なのです。
正規直交基底を見つけることは難しい
が、その便利なものを見つけることは容易ではありません。
”普通”の基底は線形独立性と生成系の関係から比較的見つけやすいこともありますが、それが【正規かつ互いに直交している】という条件は中々厳しいのです。
そこで役に立つのが「グラム・シュミットの直交化法」です。
この方法を使えば、好きなように基底を用意するだけで、機械的に正規直交基底を得ることが出来るのです。
非常に便利で、これからの応用にも必須の方法ですので、是非覚えていきましょう。
グラム・シュミットの直交化法の手順
シュミットの直交化法とは、次のような操作を指します。
基底の用意と線型独立の確認:step0
(0)まず、計量線形空間Vの元で基底であるベクトル(a1,a2,a3,…,an)を用意します。事前にこれらが線形独立であるかどうかは確かめておく必要があります。
正規化(ノルムを1へ):step1~4
(1):まず、ベクトルa1を正規化します。正規化とは、ベクトルを自分自身のノルムで割ることです。
(2):正規化されたa1はe1と書き、正規直交基底のはじめのベクトルとして考えます。
(3):次にa2を以下の手順により正規化および直交化しこれをe2とします。
(4):続いてa3,…,anを同じように正規化、直交化しそれぞれe3,…,enとします。
$$step1,2:\vec {e_{1}}=\frac {\vec{a_{1}}}{\left\| \vec {a_{1}}\right\| }$$
$$step3:\vec{e_{2}}=\frac {\vec{a_{2}}-( \vec{e_{1}} \cdot \vec{a_{2}}) \vec{e_{1}}}{\left\| \vec{a_{2}}-( \vec{e_{1}} \cdot \vec{a_{2}})\vec{e_{1}}\right\| }$$
$$step4: \vec{e_{k}}=\frac {\vec{a_{k}}-\sum_{l=1}^{k-1}\left( \vec{e_{l}} \cdot \vec{a_{k}}\right) \vec{e_{l}}}{\left\| \vec{a_{k}}-\sum_{l=1}^{k-1}\left( \vec{e_{l}} \cdot \vec{a_{k}}\right) \vec{e_{l}}\right\| }$$
これをnまで繰り返すことで、\(<e1,…,en>\)は正規直交基底となります。
直交化法の計算のコツ
グラム・シュミットの直交化法によって、ただの線形独立だったベクトルが、正規直交基底という非常に重要なものへと変化しました。
計算のコツとしては、
・Σの部分に着目すると、動いているのは既に作った基底elでありakはそのままであること、
・正規化は最後に行えばいいため、まずは分子を計算しそのノルムで割ればよいことです。
ちなみに、グラムシュミットの直交化法には図形的なイメージが存在し、計算対象のベクトルにたいして正射影ベクトルを生成しているようなものになります。
二次元平面上で試しに1パターン計算してみると感覚を掴みやすいかもしれません。
まとめと関連記事,続編へ
・正規直交基底は非常に強力な道具であるとともに、中々見つけづらい性質があります。
しかし、
・グラムシュミットの直交化法を用いれば比較的簡単に見つけ出すことが出来るため、ぜひ身に付けて使いこなせるようになりましょう!
線形代数の続編『直交行列・直交補空間と応用』
次回は、「直交行列とルジャンドルの多項式」←で”直交行列”と呼ばれる行列と、内積がベクトルや行列以外の「式(微分方程式)」でも成り立つ”応用例”を詳しく紹介します。
これまでの記事は、「線形代数を0から学ぶ!記事まとめ」←コチラのページで全て読むことができます。予習・復習にぜひご利用ください!
最後までご覧いただきまして有難うございました。
「スマナビング!」では、読者の皆さんのご意見,ご感想、記事リクエストの募集を行なっています。ぜひコメント欄までお寄せください。
また、いいね!、B!やシェア、をしていただけると、大変励みになります。
・その他のご依頼等に付きましては、運営元ページからご連絡下さい。