基底・標準基底とその周辺(0からの線形代数シリーズ)
<この記事の内容>:線型(ベクトル)空間における『基底・標準基底』の意味と、それらの変換・取り替えを図を利用して0から紹介しています。
<これまでの関連記事>:前回「部分空間(ベクトル空間)と基底・次元を解説!」では、ベクトル空間における基底の定義を紹介しています。今回の内容は主に“基底の変換”について具体的に解説したものです。
「線形代数を分かりやすく!0から学ぶ解説記事総まとめ」(必要に応じてご利用ください!)
目次(タップした所へ飛びます)
基底とは何か?
早速、『基底(きてい)』と言葉の意味から解説していきます。理解しやすいように、ここではR2(2次元)での基底を主に扱います。
が、3次以上になっても考え方は同じなので、まず2次での基底をきっちり理解するようにしましょう。
定義の復習(次の項からが本題です)
一応、前回の基底のところで紹介した定義を再掲しておきます。??な人は次の『標準基底と〜』を先にご覧ください。
『基底』の定義
定義1:線形空間Vの元(要素)を$$\vec{a_{1}},\ldots,\vec{a_{m}}$$とする時、m個の元は全て”線形独立”であること。
、かつ、
定義2:Vの任意の元(=どんなベクトルでも)を、実数$$〔k_{1},\ldots,k_{m}|k_{j}\in\mathbb{R}〕$$ と、
$$\vec{u}=k_{1}\vec{a_{1}}+\ldots+k_{n}\vec{a_{m}}$$の”線形結合の式”で表せるとき
$$\vec{a_{1}},\ldots,\vec{a_{m}}$$の”元の組”をこの”線形空間の基底”と定義します。
(引用元)当サイト内記事:「部分空間と基底・次元の定義」より
標準基底とxy座標
さて、基底の正確な定義は上の通りなのですが、(厳密さを多少犠牲にして)もう少し分かりやすく言うと、xy平面上の任意の元(:要素、ここではベクトルのことです)を表現できる2つのベクトルの組のことであると言えます。
つまり、座標上のあらゆるベクトルは基底によって表すことができ、その最も単純な例が『標準基底』(主にe1,e2,,,で表されます)です。
標準基底とは成分が$$\vec{e_{1}}=\begin{bmatrix}
1 \\
0
\end{bmatrix},\vec{e_{2}}=\begin{bmatrix}
0 \\
1
\end{bmatrix}$$のベクトルで、任意のベクトルは次のような線形結合式で示すことができます。
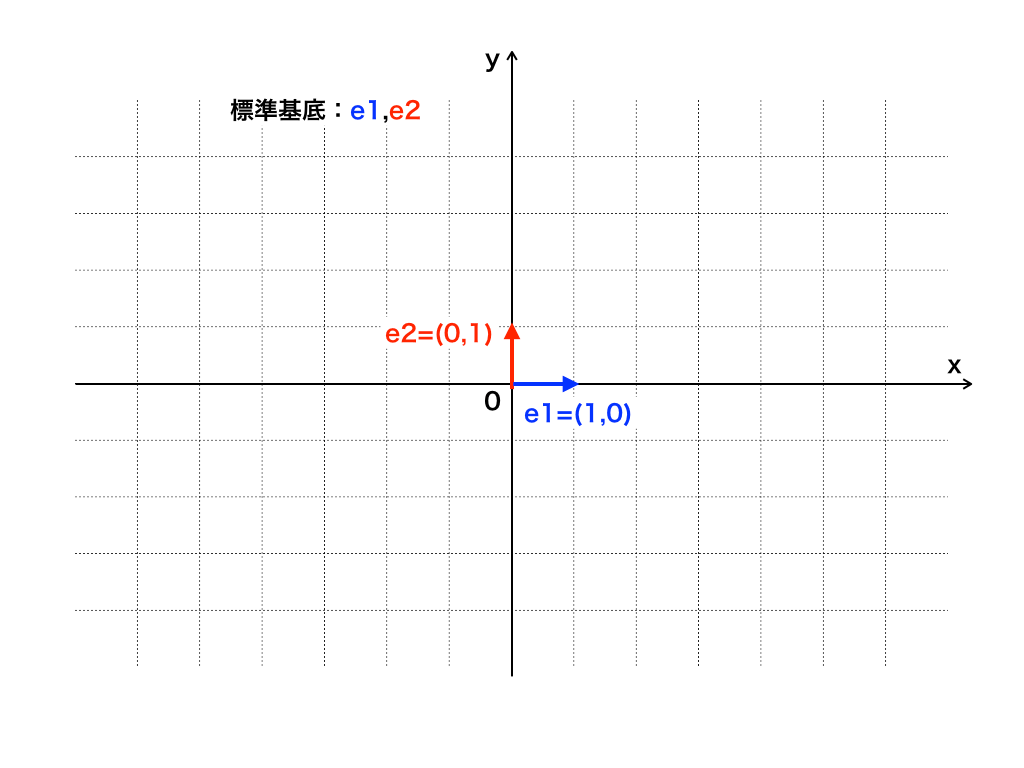
<図1:xy平面上の標準基底>
$$線形結合式\begin{pmatrix}
x & y
\end{pmatrix}\begin{pmatrix}
e_{1} \\
e_{2}
\end{pmatrix}=xe_{1} +ye_{2}$$
基底を構成する元は線形独立
以下の図を見ていただければよく分かりますが、基底が線形従属の関係にある(=線型独立でない)と任意のベクトルを示すことができません。これが最初の『定義2』で紹介したものの意味です。
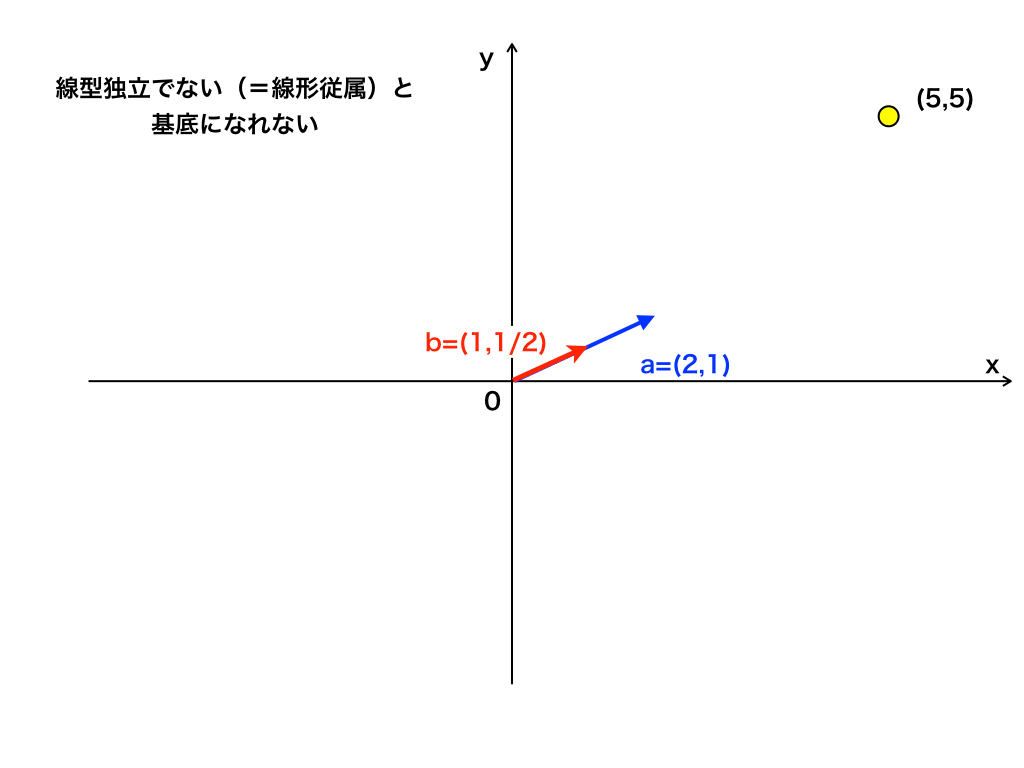
<線形従属なベクトルの組>
多次元での標準基底の表し方
ここまでは2次元での標準基底について解説してきましたが、n次元での任意の元は、『標準基底n個』を利用して、次のような式で表すことができます。
$$e_{1}=\begin{bmatrix}
1 \\
0 \\
\vdots \\
0
\end{bmatrix}e_{2}=\begin{bmatrix}
0 \\
1 \\
\vdots \\
0
\end{bmatrix}\ldots e_{n}=\begin{bmatrix}
0 \\
0 \\
\vdots \\
1
\end{bmatrix}$$1〜nまでのeを使って、
$$k_{1}\begin{bmatrix}
1 \\
0 \\
\vdots \\
0
\end{bmatrix}+k_{2}\begin{bmatrix}
0 \\
1 \\
\vdots \\
0
\end{bmatrix}+\ldots +k_{n}\begin{bmatrix}
0 \\
0 \\
\vdots \\
1
\end{bmatrix}$$
別の基底で表してみる(基底の変換)
さて、ここまでは主に標準基底でのお話でしたが、この項からは別の(標準ではない)基底で任意の元を示すことと、基底の変換について扱っていきます。
基底の変換の方法
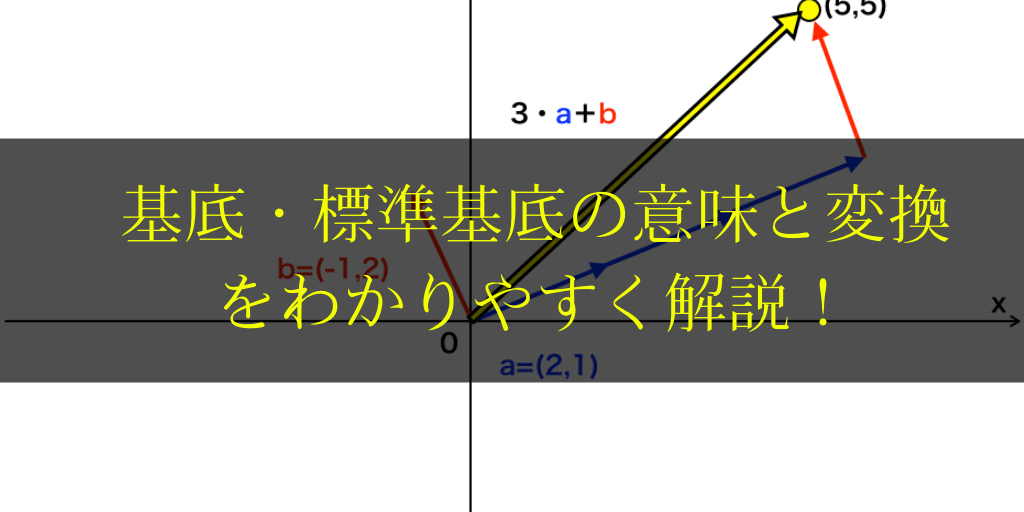
まず、以下の図を見てください。
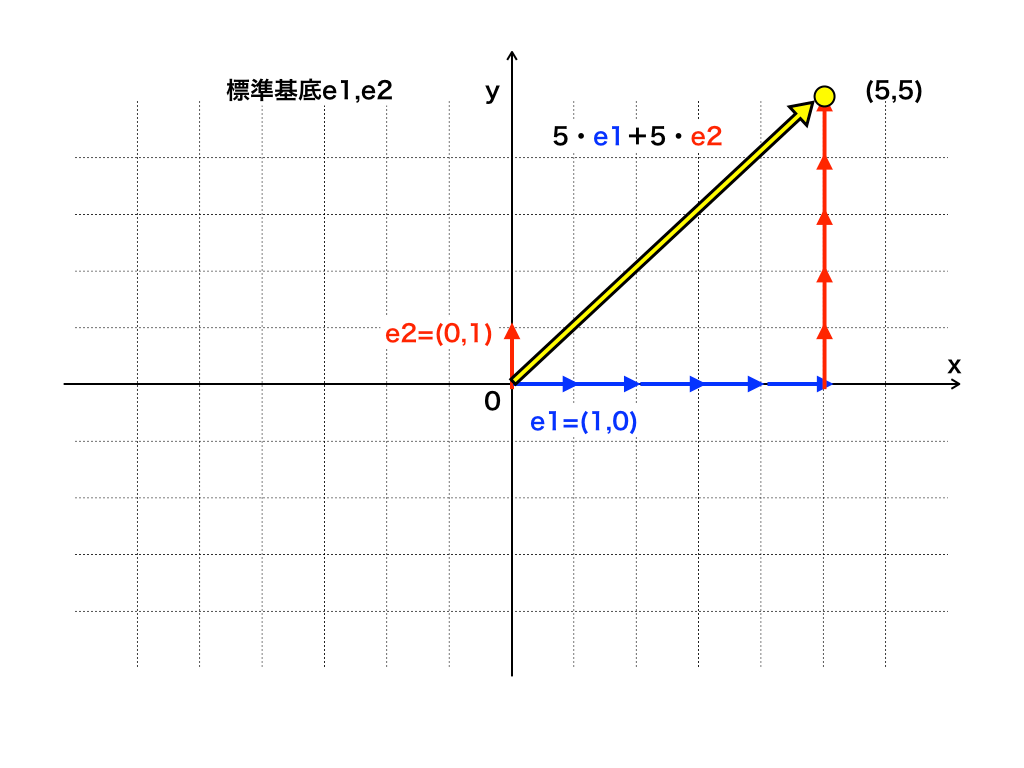
<(5,5)ベクトルを標準基底で表した図>
これは、標準基底e1とe2を使って、(5,5)のベクトルを表しています。これを新たな基底(ここでは例として次の2つのベクトルa,bを新しい基底とします)$$\vec {a}=\begin{bmatrix}
2 \\
1
\end{bmatrix},\vec {b}=\begin{bmatrix}
-1 \\
2
\end{bmatrix}$$で表す(基底を変換する)ことを考えます。
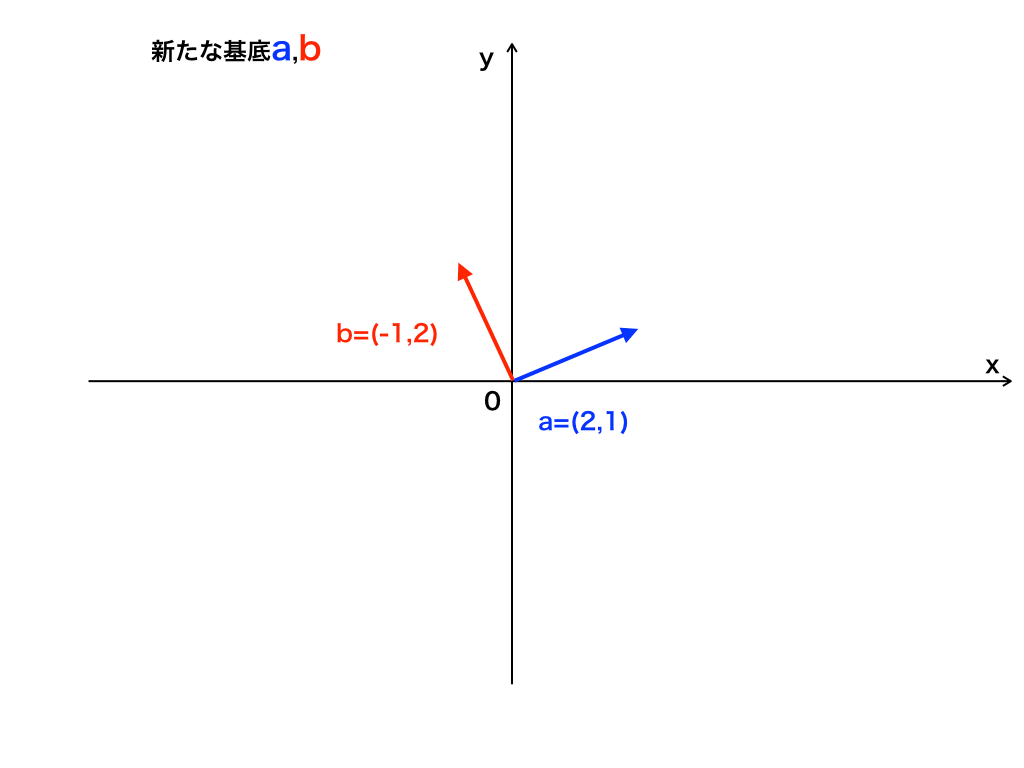
<新たな基底a,b>
基底の取り替え(変換)行列と基底の係数の求め方
ここでは、(5,5)へ基底を変換する際に必要な「行列」と、新たな基底の係数(k1,k2の部分)を求める方法とその手順を紹介します。
先に変換後の図を下に示します。
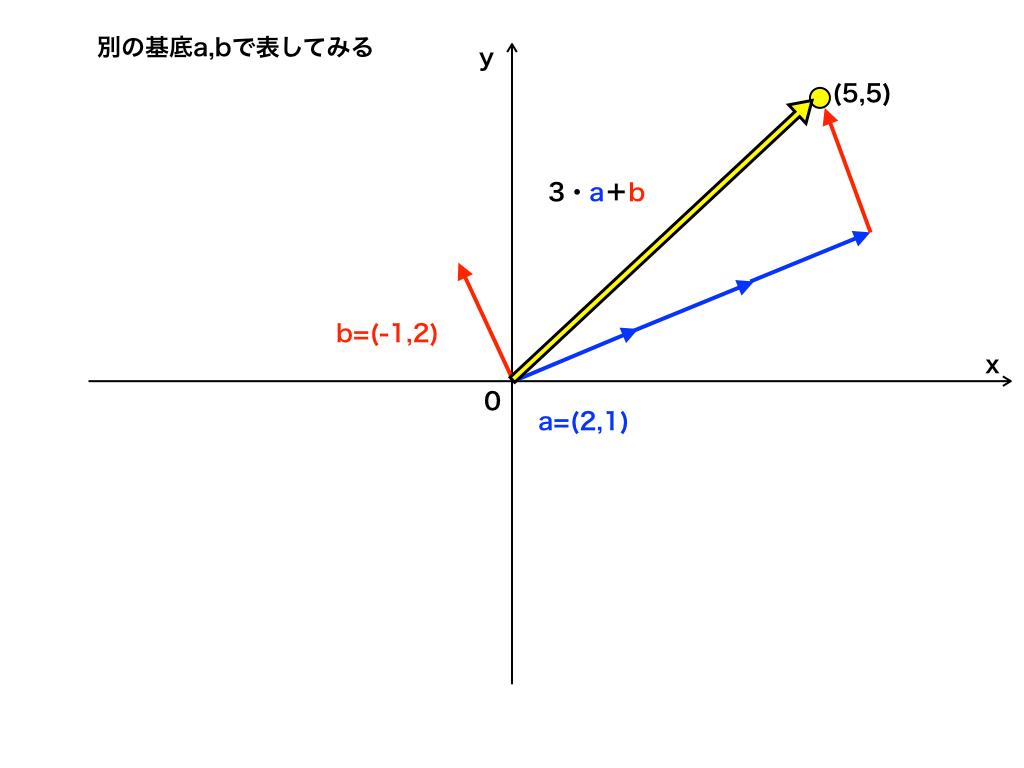
<基底を変換した後の図>
今回は簡単な2次元での変換なので、上の図より、『aの係数k1=3,かつ,bの係数k2=1』であることが分かりますが、これを行列を利用した計算で求められるようにします。
(4次元以上になると図はかけないので、行列の計算で求めることは必須です)
まず『(左辺)に、変換後の基底の列ベクトル』を並べて、『(右辺)には標準基底を並べたものに行列Fをかけた形』を作ります。
$$(\vec{a},\vec{b})=\begin{pmatrix}
\vec{e_{1}} & \vec {e_{2}}
\end{pmatrix}F=\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}F$$
この行列Fのことを『基底の取り替え(変換)行列』と言い、新たな基底のベクトルの係数を求める際に必要になります。
今回は
$$\begin{pmatrix}
2 & -1 \\
1 & 2
\end{pmatrix}=\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}F$$
となるので、両辺の行列に左から$$\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}の逆行列$$をかけることで、Fを求めることができます。
$$よって、F=\begin{pmatrix}
2 & -1 \\
1 & 2
\end{pmatrix}$$
基底の変換行列から係数を求める方法
今、新たな基底の係数が知りたかったので、$$5\vec{e_{1}}+5\vec{e_{2}}=k_{1}\vec{a}+k_{2}\vec{b}$$を掛け算の形に持ち込み、$$\begin{pmatrix}
\vec{e_{1}} & \vec {e_{2}}
\end{pmatrix}\begin{pmatrix}
5 \\
5
\end{pmatrix}=(\vec{a} \vec{b})\begin{bmatrix}
k_{1} \\
k_{2}
\end{bmatrix}$$
先ほどの標準基底とFとの関係式より、$$\begin{pmatrix}
\vec{a} & \vec {b}
\end{pmatrix}=\begin{pmatrix}
\vec{e_{1}} & \vec {e_{2}}
\end{pmatrix}F$$
これは以下のように式変形することができます。
$$\left(\begin{pmatrix}
\vec{e_{1}} & \vec {e_{2}}
\end{pmatrix}\right) \begin{bmatrix}
5 \\
5
\end{bmatrix}=\begin{pmatrix}
\vec{e_{1}} & \vec {e_{2}}
\end{pmatrix}F\begin{bmatrix}
k_{1} \\
k_{2}
\end{bmatrix}・・・(※)$$
(※)より、右辺と左辺を比べると係数を求めるには、”Fの逆行列を左から両辺に掛ければよい”ことがわかります。
従って、Fの逆行列は$$F^{-1}=\frac{1}{5}\begin{pmatrix}
2 & 1 \\
-1 & 2
\end{pmatrix}で、\frac{1}{5}\begin{pmatrix}
2 & 1 \\
-1 & 2
\end{pmatrix}\begin{pmatrix}
5 \\
5
\end{pmatrix}=\begin{bmatrix}
k_{1} \\
k_{2}
\end{bmatrix}$$
以上より、係数部分を比べて$$\begin{bmatrix}
3 \\
1
\end{bmatrix}=\begin{bmatrix}
k_{1} \\
k_{2}
\end{bmatrix}$$よって、(k1=3、k2=1)であることが求まり、この数は確かに先ほどの図での係数と一致します。

<基底の変換後の図(再掲)>
基底のまとめと線形代数の記事へ
今回は式が多く、それを追うのが特に大変だったのではないでしょうか。
理解できるまで、何度もゆっくりと読み返して見てください。
この”基底”は線形写像・固有値・固有ベクトル、そして対角化へと融合していく、線形代数において重要な概念です。
「(現在関連記事を作成中)対角化や固有値・固有ベクトルとの関係』
関連記事と線形代数まとめ記事
・「線形代数(入門・基礎)シリーズ総まとめページ」<これまでの線形代数の記事をまとめました!
内積空間(計量ベクトル)空間についての記事
固有値と対角化についての記事
最後までご覧いただきまして有難うございました。
弊サイト:スマナビング!では、読者の皆さんのご意見や、記事リクエストの募集を行なっています。ぜひコメント欄までお寄せください。
いいね!、B!やシェアなどをしていただけると励みになります。
・その他、お問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。