
ラグランジュの未定乗数法
<この記事の内容>:高校数学のレベルから、様々な機械学習の手法に必要不可欠な【ラグランジュの未定乗数法】を解説していきます。
(経済学でも未定乗数法を用いることがあるかと思います。経済学部生の方にも参考になれば幸いです。)
(「2次形式とその標準形(主成分分析のための基礎数学)」の続編です)
<対象>:未定乗数法の式の意味や、なぜ最大値を求める時に使うのかよくわからない人。
目次(タップした所へ飛びます)
ラグランジュの未定乗数法
さて、初めて機械学習の本などに触れると、このラグランジュの未定乗数法がさまざまなところに顔を出してきます。
それだけ重要な物なのですが、高校/大学と文系を選択していたり、理系出身でも卒業後しばらく時間が経つと「式の意味」からして難しく感じるかと思います。
そこで、ここからは
偏微分∂ や、ベクトル、∇(ナブラ)などの記号などを出来るだけ平易に、また必要に応じて高校数学に戻りつつ「ラグランジュの未定乗数法」を習得し、アルゴリズムの理解に専念できるように解説していきます。
(※:現在∇、多次元での未定乗数法、応用の部分を随時追加中です)
最大値を求めるラグランジュ関数と意味・注意点
ラグランジュ関数“L(x,y,λ)”は以下のように示され、(ここでのλ(ラムダ)は『ラグランジュ乗数』と呼びます。)
\(L(x,y,\lambda)=f(x,y)-\lambda\cdot g(x,y)\)
・・・(式1-1)
なんらかの条件下【ここでは関数\(g(x,y)が0\)】で、関数【f(x,y)】の最大値(最小値)の候補を求める時に使用されます。
あくまでも『候補(極値)』なので、出てきた値が”最大値であると決まっているわけではない”ことに注意が必要です。
未定乗数法の使い方と偏微分
実際に最大値を求める方法は、
\(L(x,y,\lambda)=f(x,y)-\lambda\cdot g(x,y)\)
・・・(式1-1)
において、ラグランジュ関数(1-1:左辺)を変数\(x、y、\lambda \)でそれぞれ偏微分し、
(参考:「高校数学で理解する偏微分の基礎」)
この時に求まる3本の連立方程式
$$\frac{∂L}{∂x}=0、\frac{∂L}{∂y}=0、\frac{∂L}{∂\lambda}=0$$
の解を(p,q)とすると、x=p、y=qでf(x,y)が最大値(の候補)を持つ。
なお、最後のLをλで偏微分する式を解くとg(x,y)=0(束縛条件)の式が出てきます(この理由は以下)。
(式1-1:のうち、f(x,y)の部分は、”λ”がかかっていないので定数項として消え、”-λ・g(x,y)”の”x,y”にかかっているλのみが偏微分されて\((\lambda)'=1\)となるため。)
※:具体的な例は下で扱っています。
図形(ベクトル)的な解釈
ベクトル解析では、∇は勾配を意味します。∂f(x,y)/∂とg(x,y)をそれぞれ成分として表すと、
\(∇ f(x,y)=\begin{pmatrix}
\frac {\partial f(x,y) }{\partial x} \\
\frac {\partial f(x,y) }{\partial y}
\end{pmatrix}\)
\(∇g(x,y)=\begin{pmatrix}
\frac {\partial g(x,y) }{\partial x} \\
\frac {\partial g(x,y) }{\partial y}
\end{pmatrix}\)
∇f(x,y)=λ∇g(x,y)
これは、(p,q)での2つの関数のグラフ上の法線ベクトルが並行になっていることを表しています。
(法線ベクトルが怪しい人は>>「法線ベクトルの意味を解説」)
(2,3)の成分を持つベクトルと(4,6)の成分で表示されるベクトルは向きが同じで、次のように表されるのと同じです。
\(\begin{pmatrix}
2 \\
3
\end{pmatrix}=\begin{pmatrix}
4 \\
6
\end{pmatrix}=2\begin{pmatrix}
2 \\
3
\end{pmatrix}\)
未定乗数法の例題練習と応用
実際に、簡単な練習問題を通してここまでの内容を確認していきます。
定着用例題
当サイトの「線形計画法(高校数学Ⅱ)の記事」の例題(2)を少し変更したものを使用します。高校範囲なのでそれほど難しくありません。
例題:\(x^{2}+y^{2}=5^{2}\)の下で、y=5xが最大となる(x,y)とその最大値を求めよ。
hints!:\(L(x,y,\lambda)=f(x,y)-\lambda\cdot g(x,y)\)のfやgが何に当たるかを考えて立式してみましょう。
解答解説
では、解説していきます。
まずは条件である円の方程式=g(x,y)、最大値を求める一次関数の式を=f(x,y)とします。
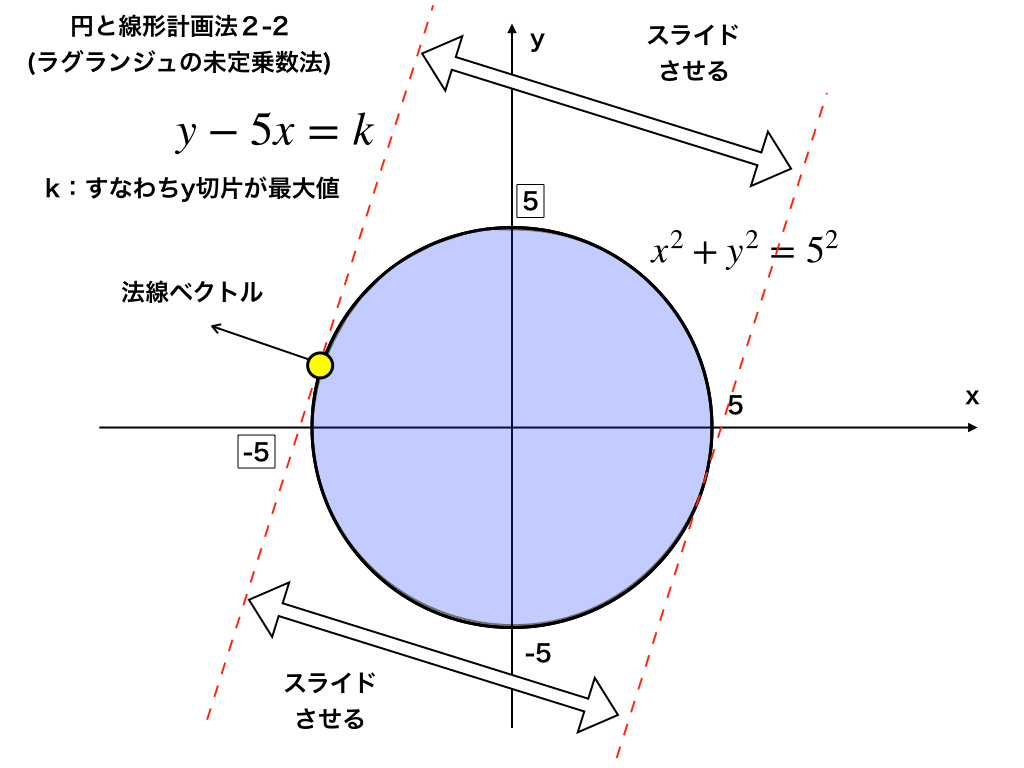
(図1)
この問題のラグランジュ関数は、\(L(x,y,λ)=(5x-y)-λ(x ^{2}+y ^{2}-25)\)
ここで、
\(∂L/∂x=5-2λx\)・・・(1)
\(∂L/∂y=-1-2λy\)・・・(2)
\(∂L/∂λ=25-x ^{2}-y ^{2}\)・・・(3)
(1)〜(3)は=0なので、
\(2λx=5\)・・・(1-2)
\(2λy=-1\)・・・(2-2)
\(x^{2}+y ^{2}=25\)・・・(3-2)
(3-2)式から、先ほど説明したように【∂L/∂λ=0】は元々の制約条件を表す事が確認できます。
x,yを求める
今我々が知りたいのは、(x,y)とその時の最大値なので(1-2)、(2-2)式を連立してλを消し(x,y)を求めます。
$$(2-2)/(1-2)=\frac{y}{x}=-\frac{1}{5}$$
よって、$$y=\frac{-x}{5}・・・(4)$$
yをxで表す事ができたので、\(x^{2}+y ^{2}=25に(4)\)を代入しxを求めます。
$$x=\pm\frac{25}{\sqrt{26}}$$
この結果を(4)に代入することでyも求まり
$$y=-\frac{1}{5}\pm\frac{25}{\sqrt{26}}$$
(∴)$$(x,y)=(\pm\frac{25}{\sqrt{26}},\mp\frac{5}{\sqrt{26}})$$
最大値を求める
(x,y)が分かったので、いよいよ本題の“最大値”を計算していきます。
これも単純で、f(x,y)に上の(x,y)を入れるだけです。
(注:xyの2組のうちどちらをf(x,y)=5x-yに入れるかですが、【-y】が有るのでyの符号がマイナスの方を使います。)
$$f(x,y)=5\cdot\frac{25}{\sqrt{26}}-(-\frac{5}{\sqrt{26}})$$
よって、\(f(x,y)=5\sqrt{26}\)・・・(答)
先ほどの(図1)のkの値(y切片)と対応しています。
機械学習のアルゴリズムへの応用
制約(拘束)条件がある状態で、関数の最大or最小値を求めることは、先述したように教師あり/教師なし学習にかかわらず色々なアルゴリズムで必要とされます。
SVM(サポートベクターマシン)/KKTなど
とくにKKTは今回解説したものの応用(制約条件が不等式で用いる)です。「SVMなどの分類(記事作成中)」でも活躍します。
下にそのほかの例をいくつか挙げておきます(追記予定)。
「線形計画法(図形と方程式)」<<定着用例題で用いた記事です。
ラグランジュの未定乗数法まとめ
今回は未定乗数法について解説しました。勾配(∇)のところは少し難しいですが、ラグランジュ関数の式(\(L(x,y,λ)=\))そのものは”それほど複雑なわけではない”ことを定着用の例題で分かって頂けたのではないかと思います。
【一度簡単な問題を手計算で解いておくと理解が定着します。ぜひ復習の際に試してみて下さい!】
この記事で出てきた”偏微分”・”最大・最小値”を求める方法、各種の最適化法は今後どんどん重要になるので、ぜひ身につけておきましょう。
関連記事一覧:機械学習+経済学のための数学へ
最後までご覧いただきまして、有難うございました。
【学習メディア】:「スマナビング!」では,読者の皆さんのご感想を募集しています。ぜひコメント欄にお寄せください。

