二次形式の意味と標準化
<この記事の内容>:線形代数で登場する「二次形式」の基本的な知識から、その標準化の手順を一歩一歩丁寧に解説しています。(二次形式はその応用・関連分野としてのPCAを理解するために重要な知識の一つです。今後数回に分けて詳しく見ていきます)
目次(タップした所へ飛びます)
二次形式とは
二次形式とは、式中の変数の次数が全て二次である式のことを言います。
ex)\(5x^{2}-4xy+5y^{2}\)は、2次の”x”、(1次のx・1次のy(="xy"←2次))、2次の”y”のみで構成されているので『二次形式』と言えます。
二次形式の定義と具体例
もう少し一般的な定義をシグマ(参考:「シグマ記号と数列の和の意味」)を使って表してみます。
行列での二次形式の表現と例
上で紹介した二次形式の例(ex)\(5x^{2}-4xy+5y^{2}\)を『行列の積のかたち』であらわしてみます。
(ここからいよいよ『線形代数』らしくなってきます。復習したい方は→「行列どうしの掛け算(積)を分かりやすく」)
各係数を比較して、次の3つの行列(2つの列・行ベクトルと1つの正方行列)の積にすれば上手く元の二次形式になります。
$$\begin{bmatrix}
x & y
\end{bmatrix}\begin{bmatrix}
a_{11} & a_{12} \\
a_{12} & a_{22}
\end{bmatrix}\begin{bmatrix}
x \\
y
\end{bmatrix}$$
より、\(\begin{pmatrix}
x & y
\end{pmatrix}\begin{pmatrix}
5 & -2 \\
-2 & 5
\end{pmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix}\)
これが正しいのかは実際に展開していくとチェックできます。
二次形式の標準形
さて、ここまで扱ってきた2次形式は“xy”という項が邪魔をして、我々が知っている「二次曲線の形(楕円)」になりません。そこで、\(ax^{2}+by^{2}\)の形にする作業を”標準化”と言います。
標準化の手順と直交行列の復習
2次形式の標準化には、「直交行列U」を用います。詳しくは→「直交行列の性質」
(具体例)二次形式を標準形にする手順
では実際に、先ほどから例示している\(5x^{2}-4xy+5y^{2}=8\cdots (※)\)という二次形式を標準化していきます。
途中少し複雑なところもありますが、とりあえず『流れ』を頭に入れるようにしてください。
(以下で固有値・固有ベクトルを扱います。参照:「固有値問題の解説記事」)
固有方程式を解く(step1)
行列の積で表した(※)の左辺は次のようになり、中心の正方行列\(\begin{bmatrix}
5 & -2 \\
-2 & 5
\end{bmatrix}\)をAとします。
\(\begin{bmatrix}
x & y
\end{bmatrix}\begin{bmatrix}
5 & -2 \\
-2 & 5
\end{bmatrix}\begin{bmatrix}
x \\
y
\end{bmatrix}\)
\(|T|= |A-\lambda E|=0\)を解くと、
\(\begin{vmatrix}
5-\lambda & -2 \\
-2 & 5-\lambda
\end{vmatrix}=\lambda^{2}-10\lambda+21\)
よって、固有値λ=3,7。
固有ベクトルを求め正規化する(step2)
(Ⅰ):λ=3の場合
ここから、それぞれの固有ベクトルを求めていきます。
\(\begin{bmatrix}
2 & -2 \\
-2 & 2
\end{bmatrix}\begin{pmatrix}
m_{1} \\
m_{2}
\end{pmatrix}=\begin{pmatrix}
0 \\
0
\end{pmatrix}\)
上の式を展開して\(m_{1}-m_{2}=0\)
ランクが1なので、(「階段行列とランク・自由度を解説」)
\(m_{2}=k_{1}とおくとm_{1}=k_{1}\)
したがって、\(\vec{x_{1}}=k_{1}\begin{pmatrix}
1 \\
1
\end{pmatrix}\)
ここで、ノルムを1にする:つまり正規化を行います。\(\left(||\vec{x_{1}}||\right)=\sqrt{2}\)だから、
\(k_{1}=\frac{1}{\sqrt{2}}\)と置けば良いことがわかります。
よって$$\vec{x_{1}}=\frac{1}{\sqrt{2}}\begin{pmatrix}
1 \\
1
\end{pmatrix}$$
が求まりました。
(Ⅱ):λ=7の場合も上の同様に進めていきます。
\(\begin{bmatrix}
-2 & -2 \\
-2 & -2
\end{bmatrix}\begin{pmatrix}
n_{1} \\
n_{2}
\end{pmatrix}=\begin{pmatrix}
0 \\
0
\end{pmatrix}\)
結果、$$\vec{x_{2}}=\frac{1}{\sqrt{2}}\begin{pmatrix}
-1 \\
1
\end{pmatrix}$$
となります。
直交行列Uと\(U^{-1}\)で挟む:\(U^{-1}AU\)(step3)
以上の結果から、直交行列\(U=\frac{1}{\sqrt{2}}\begin{pmatrix}
1 & -1 \\
1 & 1
\end{pmatrix}\)となって、AをUの逆行列を左から、Uを右から挟んであげることで
\(U^{-1}AU=\begin{pmatrix}
3 & 0 \\
0 & 7
\end{pmatrix}\)
(対角成分は固有値となります)
変数変換して二次曲線の形へ(step4)
最後に、”x”と”y”で表されていた(※)の二次形式を【x'とy'】に変換します。
列ベクトル:\(\begin{pmatrix}
x \\
y
\end{pmatrix}=U\begin{pmatrix}
x' \\
y'
\end{pmatrix}\)と行ベクトルで\(\begin{bmatrix}
5 & -2 \\
-2 & 5
\end{bmatrix}\)を挟むために、\(\begin{pmatrix}
x \\
y
\end{pmatrix}\)を転置させます。
\(\begin{pmatrix}
x \\
y
\end{pmatrix}^{T}=\begin{pmatrix}
x' & y'
\end{pmatrix}U^{T},かつU^{T}=U^{-1}\)
(∵)直交行列の性質
より、\(\begin{bmatrix}
x & y
\end{bmatrix}\begin{bmatrix}
5 & -2 \\
-2 & 5
\end{bmatrix}\begin{bmatrix}
x \\
y
\end{bmatrix}\)
の両側のベクトルを置き換えていきます。
\(\begin{bmatrix}
x' & y'
\end{bmatrix}U^{-1}\begin{bmatrix}
5 & -2 \\
-2 & 5
\end{bmatrix}U\begin{bmatrix}
x' \\
y'
\end{bmatrix}\)
ここで、\(U^{-1}AU=\begin{bmatrix}
3 & 0 \\
0 & 7
\end{bmatrix}\)だったので(step3より)
5つ並んだベクトル・行列の積のうち真ん中の三つが消えて最終的に
\(\begin{bmatrix}
x' & y'
\end{bmatrix}\begin{bmatrix}
3 & 0 \\
0 & 7
\end{bmatrix}\begin{bmatrix}
x' \\
y'
\end{bmatrix}\)となります。これを行列の積のルールに沿って展開していくと、
\(\begin{bmatrix}
3x' & 7y'
\end{bmatrix}\begin{bmatrix}
x' \\
y'
\end{bmatrix}=3x'^{2}+7y'^{2}\)
あとは、右辺=8だったので、\(3x'^{2}+7y'^{2}=8\)とすると確かに”xy”の項が消えて上手く楕円の式(二次曲線の式)の形にすることができました。
(お疲れ様でした!あとは今回の結果の幾何的な意味を見ていきましょう。この複雑な操作が非常に美しい意味を持つことが分かるかと思います。)
標準化を視覚的に理解する
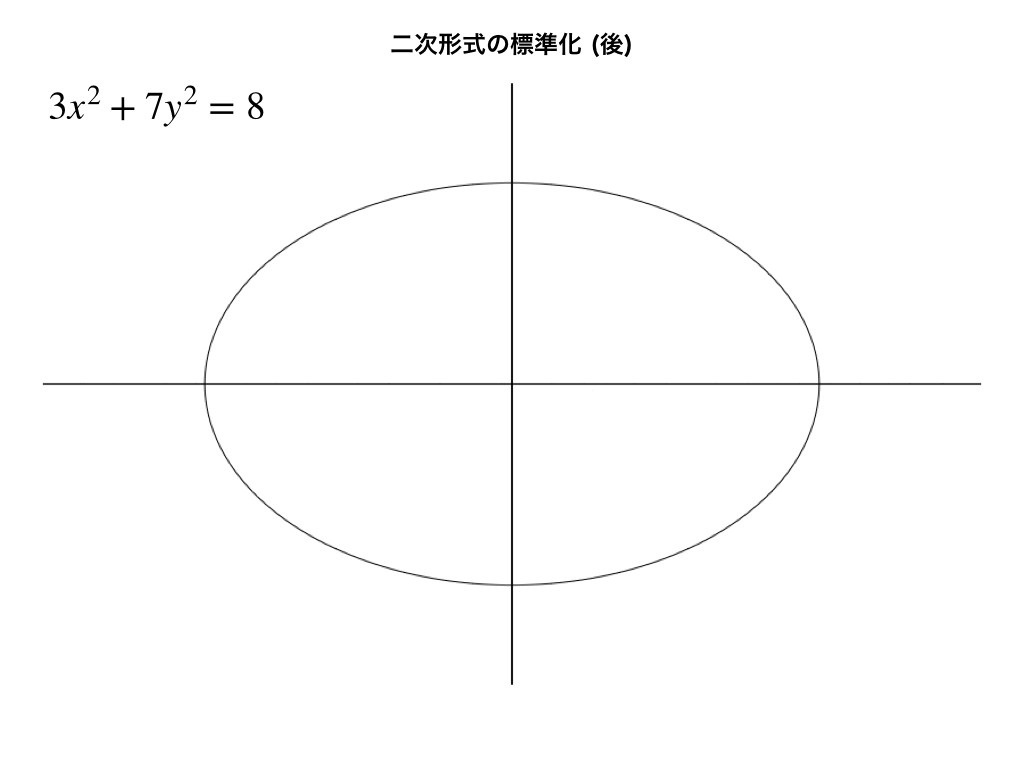
さて、ここまで少し(かなり?)大変でしたが、二次形式\(5x^{2}-4xy+5y^{2}=8\)を\(x^{2}+y^{2}=8\)に”標準化”することが出来ました。
これは一体どのような意味を持つのか、視覚的にとらえてみます。
前;斜め向きの楕円
まずは標準化する前の(※)の二次形式を座標平面上に描くと
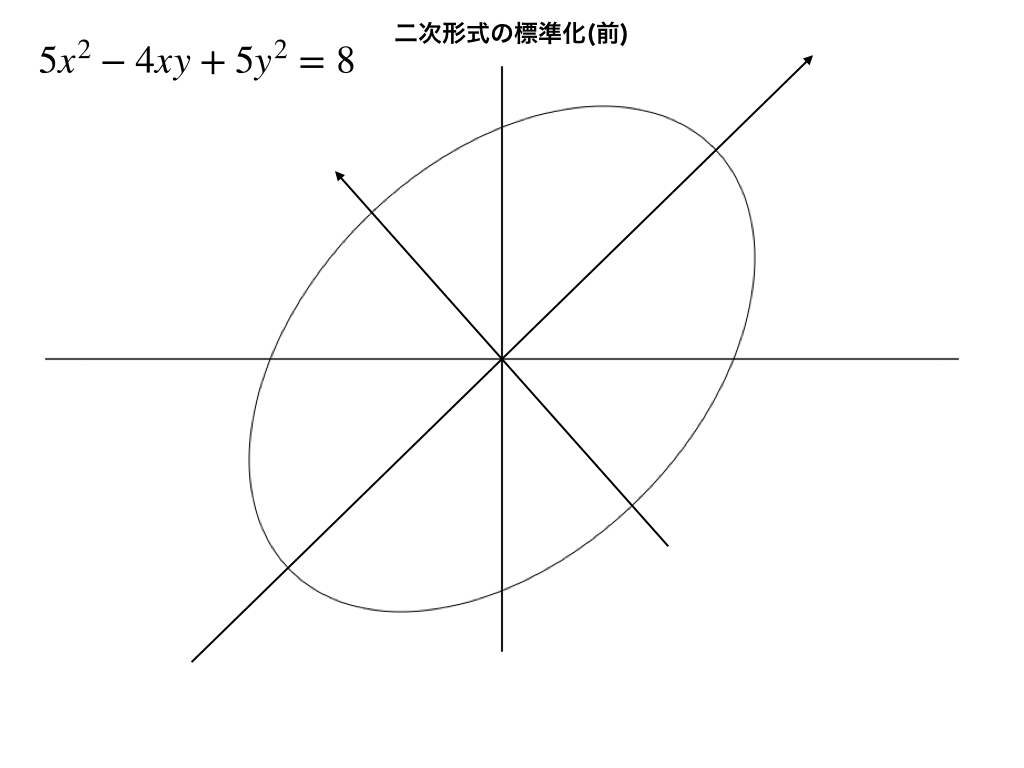
形は楕円ですが、長短軸が斜めになっています。
後:軸と長軸/短軸が一致
さあ、標準化後の\(x^{2}+y^{2}=8\)を同様に描くと・・・
主軸変換:前後を重ねてみると・・・
青色で示した標準化後の\(x^{2}+y^{2}=8\)青色の楕円は元々の\(5x^{2}-4xy+5y^{2}=8\)と
・大きさ
・角
が同じで軸のみが回転している様子がわかります。
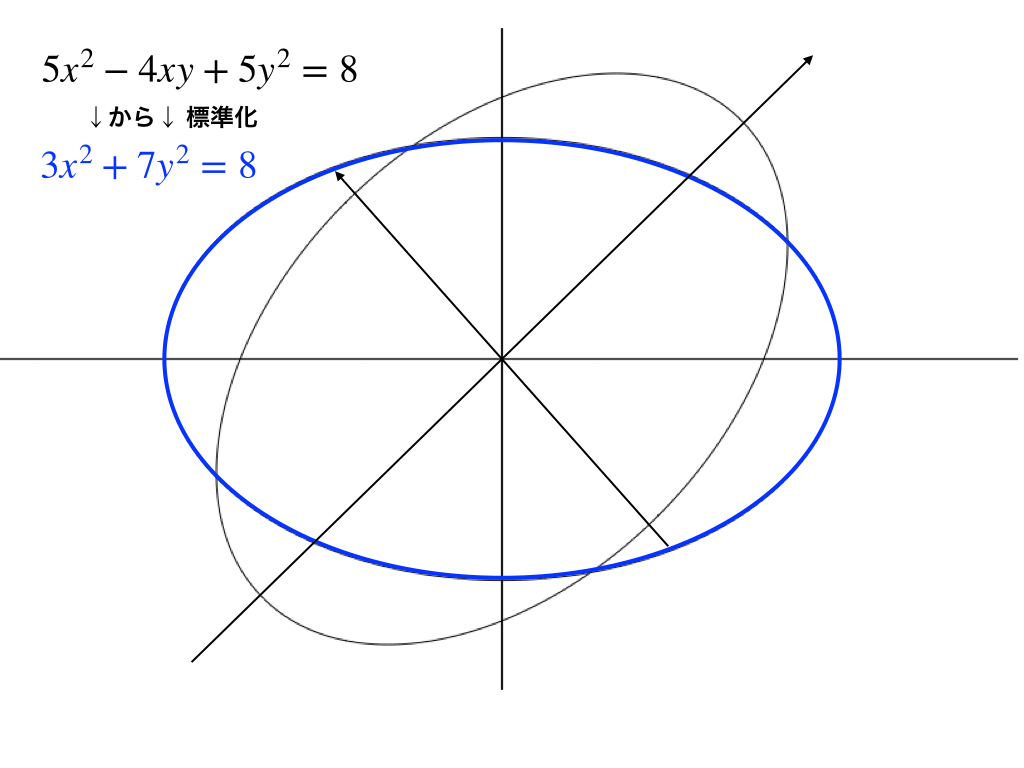
<二次形式の変換前後>
二次形式まとめと主成分分析へ
・今回は直交行列を用いて二次形式を変換する作業を行いました。
・手順が多く大変なので、実際に手を動かして練習したりテキストなどで問題を解いて慣らせていきましょう。
・最後にグラフで見た『主軸』の変換(二次曲線の回転)が今後学習する『主成分分析』の基礎の一つとなります。機械学習の理論を勉強している方はこのイメージを頭に入れておきましょう。
関連記事と〜共分散行列へ〜
続編:「ラグランジュの未定乗数法の解説」
「(作成中)共分散行列とPCA」
最後までご覧いただきまして、まことに有難うございました。
【学習メディア】:「スマナビング!」では,読者の皆さまのご感想を募集しています。ぜひコメント欄にお寄せください。
(※:個々の問題・証明の質問などには対応出来ない場合があります)
・その他の「お問い合わせ/ご依頼/タイアップ」等に付きましては、運営元に直接ご連絡下さい。