
絶対値が含まれる問題を攻略!
あなたは「絶対値」が問題文中に入っていた時「解くのが大変そうだ」、
「一旦飛ばして違う問題を解こう」などと考えていませんか?
この記事では、絶対値つき問題を解くたった1通りの解法を紹介しています。
他の人が苦手意識を持つ絶対値を攻略することで、大きく差をつけることが出来ます。
ぜひじっくりご覧ください。
目次(タップした所へ飛びます)
絶対値とは
はじめに、絶対値の基本的な意味を確認しておきます。
定義:「絶対値は原点からの距離」
ごくごく簡単な定義ですが、テストなどで問題を解いていると絶対値記号ばかりを気にしてしまい
この定義を思い出せない人が少なくありません。
難問にぶつかったらこの”定義”を思い出してみると新たな糸口が見つかることもあります。
絶対値の定義と数直線
この定義を図で見ていきましょう。以下の<図1>は、
|x|=3、|x|<3、|x|>3のそれぞれの場合を数直線で表したものです。
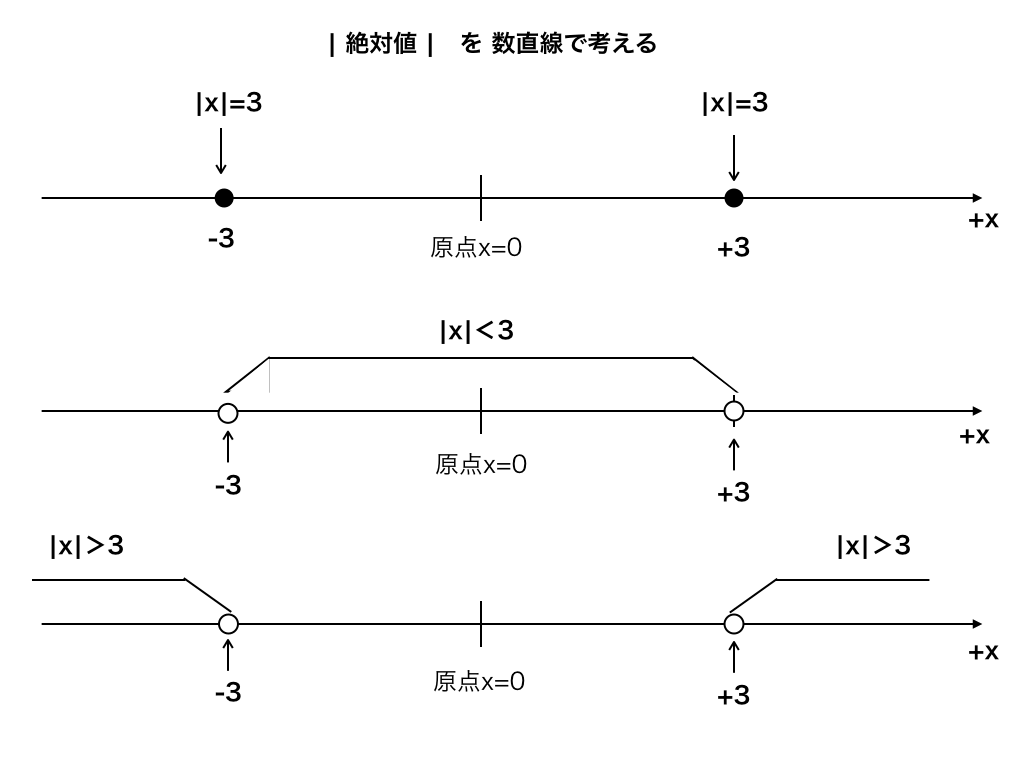
<図1:絶対値と数直線>
絶対値の問題が好んで出題される理由
これは簡単に難易度を上げることができる事と、以下で解説する「しっかりと場合分けをしてミスをしないか」と言った点を判断できるからです。
それゆえ、絶対値と融合しない分野はほとんどなく、数と式(今回解説します)、整数、場合の数/確率から指数/対数、極限、微積分の応用まで、どの分野でも絶対値付きの問題を見つけることができます。
絶対値付き問題の解法(場合分け)
絶対値が関係するの問題の解き方は「絶対値の中身の正負で場合分け」するタイプが主になります。
場合分けをして絶対値を外す
ここでは、場合分けをする絶対値の具体的な問題を見ながら解法を解説していきます。
基本的な考え方
|中身が正となる式|ならば、そのまま絶対値を外す。
|中身が負となる式|ならば、マイナスをつけて(掛けて)外す。
絶対値つき方程式の解を場合分けをして求める問題
最も基本的で、よく見るタイプの『絶対値付き方程式』を解く問題を解いていきましょう
(問0):|x-2|=0の式を満たすxの値を求めよ。
簡単すぎると思われるかもしれませんが、
複雑な式になったときでも応用できるように一番基礎のレベルから解説していきます。
このたぐいの問題では、絶対値は必ず0以上であることを利用して、|絶対値の中身|が0以上か0未満か、に分けて考えます。
(ⅰ)(x-2)≧0の時、すなわちx≧2の時、|正|なので、そのまま絶対値を外します。
x-2=0より、x=2
これは、条件x≧2を満たすので方程式の解です。
(ⅱ)(x-2)<0、つまりx<2のとき、|絶対値の中の式|にマイナスをかけて外します。
よって、-x+2=0とします。すると、x=2となりますが
、これはxが2未満であるという条件に反するので、解ではありません。
従って、x=2・・・(答)
(問1)|x-4|+|x-3|=2 の式を満たすxを求めよ。
絶対値が2つになりましたが、やることは同じです。
2つの絶対値が正・負になる境目で場合分けする。
|x-4|+|x-3|=2 この式を見たら、x=4とx=3がそれぞれの絶対値の中身の“境目”になることがわかります。
したがって、xが4以上、xが3以上4未満、xが3未満、の3通りに分けて絶対値を外すことを考えます。
(一)x≧4のときは|x-4|も|x-3|の中身両方正なので、そのまま外します。
x-4+x-3=2
より、2x=9 x=9/2
はじめの条件:x≧4をx=9/2は満たすので、x= 9/2。
(二)3≦x<4のとき、|x−3|は正ですが、|x-4|は負なので、(x-4)にマイナスをかけて絶対値を外します。
結果-(x-4)+(x-3)=2 となりますが、右辺=1、左辺=2となって右辺≠左辺となり、矛盾します。よって不適。
(三)x<3 のとき、| x-3|と|x-4|はともに負となるので、(x-3),(x-4)の両方にマイナスをかけて外します。
ーx +4ーx+3=2
ー2x=ー5 より、x=5/2
これは、x<3の条件を満たしている。
以上の(一)〜(三)をまとめて、x= 9/2,5/2・・・(答)
絶対値付き方程式の解の個数を調べる問題(定数分離)
(問2): |x2+2x|ーa=0の方程式の解の個数を求めよ。(ただし、aは定数である)
<関連:「二次関数のグラフと解の存在範囲」>
今回はいわゆる“定数分離型“の解法でといていきます。
これは、xの次数が0=ここでは定数aをxの式と分けて、
それぞれをxy座標上のグラフに表して解く方法です。すなわち
y=|x2+2x|ーaのグラフを、
・y=|x2+2x | ・・・(1)と
・y=a・・・(2)
の二つに分離して、(1)(2)が交わった個数=題意の解の個数となります。
具体的に図を見ながら解いていきましょう。
※絶対値つきのグラフを書くコツ
(1)の形のように、絶対値の中に|xの式|が入っている関数のグラフは、
必ずy=0(=x軸)のところで折り返します。(つまり、グラフがy=0より小さな値をとることがない)。
y=|x| のグラフ(下の図)を見てもそれが確認できます。
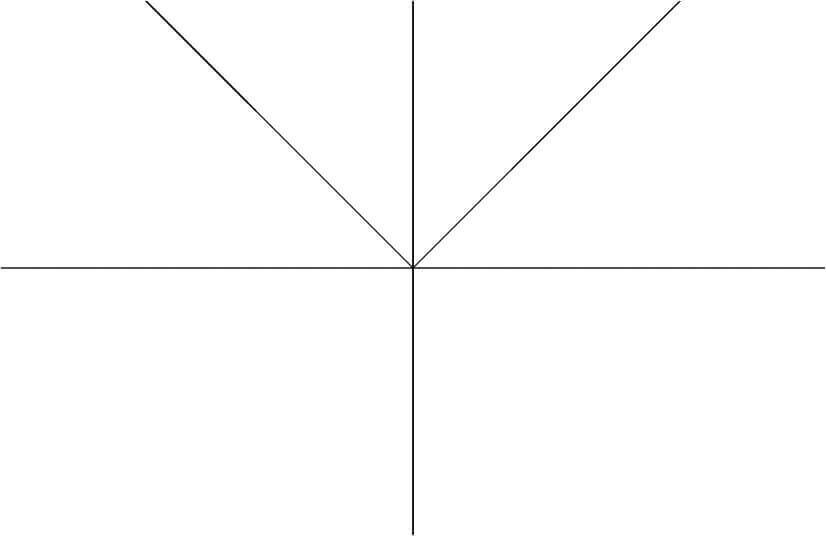
<y=|x|のグラフ>
理由:その理由はいたって単純で、この記事の一番最初で述べたように、
そもそも絶対値は「原点からの距離を表す」ものであり、距離が負になることはありえないからです。
従って、絶対値の中に入っているxの関数のグラフも負の値を取らず、x軸(y=0)のところで
y軸正方向に180°折り返すのです。
では問2の解説に戻ります。
上のコツを使ってグラフを書くと、y=|x2+2x|=|(x+1)2-1| と平方完成し、
x軸のところで折り返すだけで描く事が出来ました。
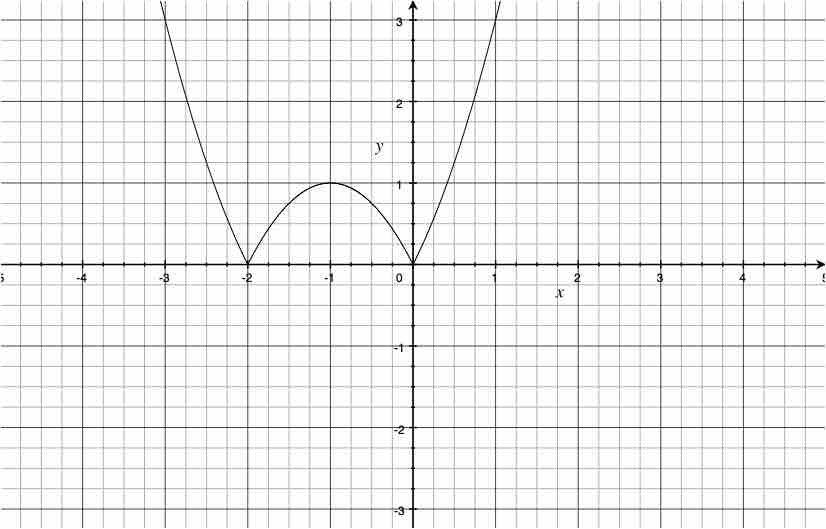
<(1)y=|x2+2x|のグラフ>
定数分離と交点の個数
残りは、(2)のy=a ですが、この式の意味はa=0の時、グラフはy=0;x軸
a=2の時、グラフはy=2、、、とaの値に合わせてx軸に平行に上下することを意味します。
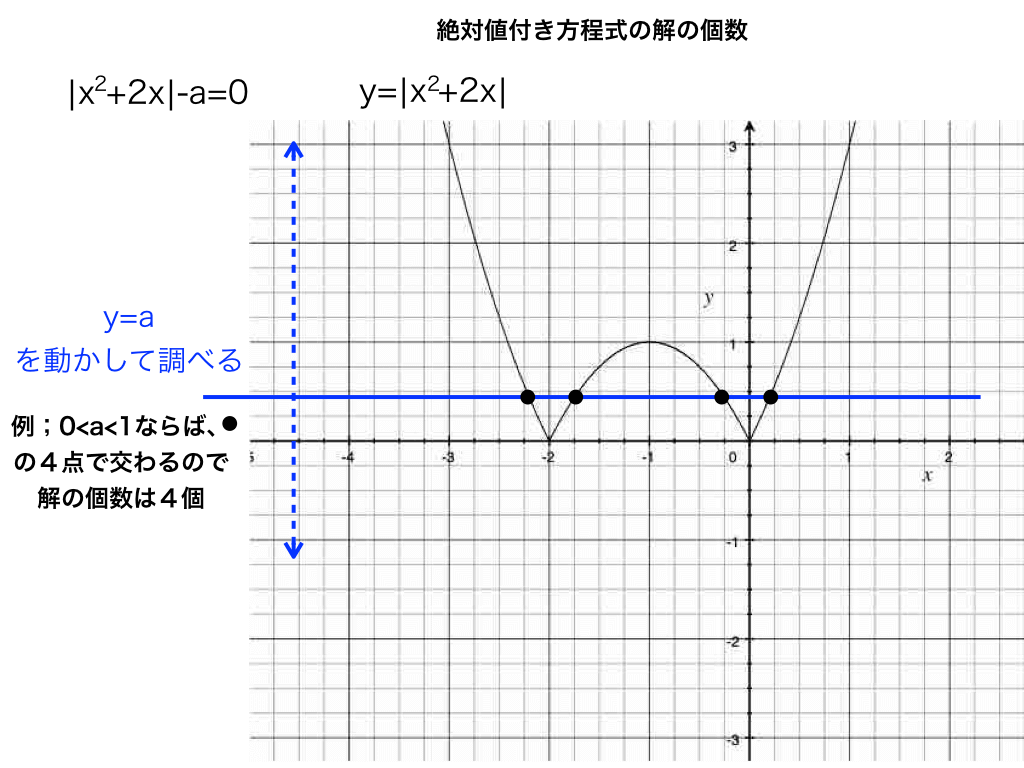
<(1)のグラフ上で(2)を動かす↑>
今、元の式(0=|x2+2x|-a)の解の個数を求めたいので、
(1)のグラフ上でy=aを動かして、aの値の範囲によって変化する、交点の数を調べるだけで解く事が出来ます。
よって、a=0のときy=|x2+x|のグラフとの交点は2点(x=-2,0)あり、
0<a<1のとき交点は4つ
a=1のとき交点は3つ(折り返した二次関数の頂点(1,-1)と、(0,1),(-2,1)の三点で交わっています。
1<aのとき交点は2つ
存在することがグラフからわかります。
そして、グラフ中のy=| x2+2x|とy=aの交点の個数が与式の解の個数と一致することから、
<解答>
| x2+2x|-a=0の方程式の解の個数は、
(1)a<0のとき、解は0個
(2)a=0のとき、解は2個
(3)0<a<1のとき、解は4個
(4)a=1のとき、解は3個
(5)2<aのとき、解は2個・・・(答)
これらの(1)〜(5)が答えとなります。
絶対値のまとめと関連記事(整数分野と方程式)
・絶対値の問題はまず「中身の正負で場合分け」して外す。
・絶対値の応用範囲は高校数学ほぼ全てなので、今後も少しずつ融合問題の解説記事を増やしていきます。
<<関連記事:「整数問題の解法・解説まとめ」>>
以下の記事で様々な方程式・不等式の解き方を網羅していますぜひ参考にしてください!
>>「高校数学で学ぶ方程式/不等式の解法総まとめ」<<
今回も最後までご覧いただきまして、本当に有難うございました。
当サイト「スマホで学ぶサイト、スマナビング!」は日々改善、記事の追加、更新を行なっています。
読みたい記事のリクエストや、ご質問・ご意見がございましたらコメント欄にお寄せください。
また、snsでいいね!やシェア、Twitterのフォローをしていただけると助かります。

