
確率漸化式の作り方入門
これから詳しく解説していきますが、確率漸化式は数列の漸化式と場合の数/確率が融合した分野で、難しく感じる人が多いです。
しかし、実際には解法の数は多く無いので、食わず嫌いで捨ててしまうのは非常にもったいない分野なんです。
この記事で確率漸化式の基本を習得して、「応用編の確率(連立)漸化式の記事」を読んでもらえれば、全く手がつけられない問題は無くなります。
また、そもそも「数列の漸化式」が苦手だ!という人向けの記事も用意しているので、殆ど知識が無い状態でも大丈夫です。
では、はじめましょう。
(確率漸化式の応用編:連立漸化式を解く問題を追加しました。)
目次(タップした所へ飛びます)
確率漸化式は場合の数・確率と数列の融合分野
また、数列の極限とも合わせて出題されるので文系/理系問わず確実に攻略しておきたいところです。
確率の問題はレベルが上がるにつれて、殆どの問題文の条件に”時間や回数の推移による変化“が含まれる様になってきます。
以前解説した反復試行の様に、「ある操作をn回した時〜の確率は・・・」の様な感じです。
そして、ある条件の下で「前後関係(n回目とn+1回目の様に)を表すのに使われるのが漸化式」です。
確率漸化式の作り方を例題で見て行きます。
※本問では簡単な漸化式を解くので、数列分野を学習済みの方が望ましいです。(近いうちに数列シリーズ執筆予定)数列の漸化式の解き方シリーズ作成しました!
(例題1)
1から10までの数字が書かれた球を袋に入れて、1回につき1個取り出し、その球に書かれた番号を記録して袋に戻す。
この試行をn回繰り返す時、5の倍数(5、10)の球が奇数回取り出される確率を求めよ。
一見何から取り掛かればいいか分からなくなりそうですが、n回目の確率を問われているのでこういう場合には確率漸化式を疑ってみます。
コツ:n回目の確率→n回目とn+1回目の推移図を描き漸化式を作る
n回目の試行を数列の第n項、n+1回目を第n+1項に対応させて、一般項PnとPn+1の式を作ります。
具体的には以下の様な推移図を書いていきます。
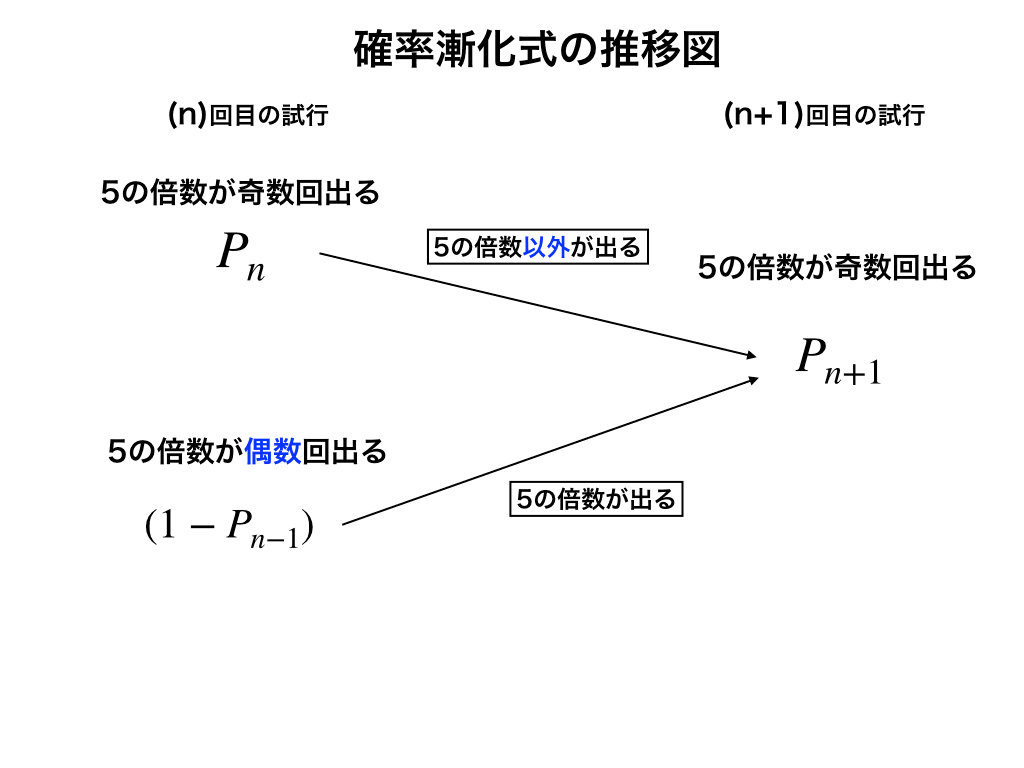
<確率漸化式の推移図>
まず求める確率をPnとして、n回目の時点で5の倍数(5、10)が奇数回でた確率をPn、偶数回出た確率を(1-Pn):「これはPnの『余事象』の考え方です」とおきます。
更に、もう一回試行してPn+1になる為には
n回目の時点で奇数回の時は5の倍数以外、
n回目の時点で偶数回の時は5の倍数が出る必要があるから、
Pn×8/10+(1-Pn)×2/10=Pn+1
$$P_{n+1}=P_{n}\times \frac {8}{10}+(1-P_{n})\times \frac {2}{10}$$
とおけます。これを解いた一般項:Pnが「n回目に5の倍数が奇数個出る確率」となります。
ここから漸化式(特性方程式type)を解いていきます
このタイプの漸化式の解き方は右の記事で解説しています。→等比数列帰着型の漸化式の解き方
Pn+1=3/5Pn+1/5
$$p_{n+1}=\frac {3}{5}p_{n}+\frac {1}{5}$$
特性方程式より、
(Pn+1-1/2)=3/5(Pn-1/2)
$$\left( p_{n+1}-\frac {1}{2}\right) =\frac {3}{5}\left( p_{n}-\frac {1}{2}\right) $$
(Pnー1/2)=Cnと置いて
$$\left( p_{n}-\frac {1}{2}\right) =c_{n}$$
Cn+1=3/5Cn
$$C_{n+1}=\frac {3}{5}C_{n}$$
ここで、p1、即ち1回試行した時(奇数回=1回)5の倍数が出る確率は、2/10
よって初項P1=2/10 C1=-3/10
Cn=(3/5)^(n-1)×(-3/10)
$$C_{n}=( \frac {3}{5})^{n-1}\times (-\frac {3}{10}) $$
$$p_{n}=\left( -\frac {3}{10}\right) \left( \frac {3}{5}\right) ^{n-1}+\frac {1}{2}$$
実際に確認してみると、
n=1 のときP1=2/10=1/5 となり正しいことがわかります。
ここから数学Ⅲ:数列の極限と融合させます(理系向け)
数列の極限については次のリンクに有る極限シリーズで詳説しています。→数列の極限がわかる!
更に、この試行を無限回行う(n=∞)とき
$$\lim _{n\rightarrow \infty }p_{n}=\left( -\frac {3}{10}\right) \left( \frac {3}{5}\right) ^{n-1}+\frac {1}{2}$$
となって、
無限回この試行を行うと、問題の確率は(lim(n→∞)Pn=)1/2 になることがわかります。
まとめと確率漸化式の応用題/類題へ
この様に、文理共通で確率漸化式の問題が出て、文系数学ではPnを求めて第n回での確率を求めさせるところまで、理系数学は更にプラスαとして数列の極限等を最後に持ってくることが良くあります。
いずれにせよ、確率漸化式は文理問わず最重要分野な上、色々な出題パターンが有るので、沢山の問題にふれて是非得意分野にしましょう。
続編完成しました!以下より続けてご覧下さい!→連立確率漸化式(解く漸化式が連立漸化式の時)
お役に立ちましたら、snsボタンよりシェアお願いします。また、公式Twitterは→@linkyjuku_tweet


