
微分方程式と高校物理・数学シリーズ(1)
今日は微分方程式を取り上げます。と言っても、
理系受験生や、進度の早い生徒なら高校2年生位でも取り組めるように入門レベルの説明から初めます!
(数学Ⅲの積分の基礎計算が出来れば充分です。もしまだ数学Ⅲの積分未習でも、
近日中にフォロー記事をアップするので、
(作成しました。わからないところがあれば上の記事まとめの中から探してみてください。)
目次(タップした所へ飛びます)
微分方程式(1)今回の到達目標
・そもそも微分方程式って?の状態から、
・変数分離型の微分方程式を解けるようになる
・微分方程式で運動方程式が記述できるようになる
・古典物理学~Newton力学の中でも初歩的な雨粒の自由落下(空気抵抗アリ)の例を通して、
微分方程式がどう役に立つかを確認する
・オマケ:微分積分学の歴史と蘊蓄に少し詳しくなれる
では始めましょう!
微分方程式って何?
例えば、x2+5x+6=0 これはXの2次方程式
∫1→3 f(t)dt=定数 ならば積分に関する方程式(インテグラルが入っているからです)すなわち積分方程式。
積分方程式については右の記事で詳しく解説しています。→「積分方程式の意味とたった2通りの解法」を学ぶ。
dy/dx=(2y−3)x これは左辺にy‘、つまり導関数が含まれているので微分方程式。
これだけです。式に微分が入っている式です。ただこの単純な式がありとあらゆる現象を説明し利用されているのです。
微分方程式が無ければ今皆さんの持っているスマホも、コンピューターも、それらで計算され作られた電化製品も何もかも無い事でしょう。
でもそれは大学以降のお話です。
取りあえず最も単純な『変数分離型の微分方程式』を解けるようになりましょう。
変数分離型の微分方程式の解き方
記事を見ながら手を動かして計算について来て下さい!
dy/dx=(2yー3)x 上にのせた微分方程式です。
これをyとdyは左辺へ、xとdxは右辺へ分離します。(だから変数分離型といいます)そして両辺にインテグラルを付けてyはy、xはxで不定積分します。
$$\frac{dy}{dx}=(2y-3)x⇔\frac{dy}{(2y-3)}=xdx$$
$$\int \frac {1}{\left( 2y-3\right) }dy=\int xdx$$
両辺不定積分を行なって、式を整理すると、
\(\log\left| 2y-3\right| =x^{2}+2C\)(ただしCは積分定数)
次に対数を外して、|絶対値|=の形に変形します。
\(|2y-3|=e^{x^{2}+2C}\)さらにこの式から絶対値を外して、$$y=\frac{1}{2}(±e^{2C}・e^{x^{2}}+3)$$
ここで、ネイピア数の積分定数乗されている±e2C←この部分は、新たな積分定数C1とおいても問題ないので、結局この微分方程式の解は以下のようになります。
$$y=\frac{1}{2}(C_{1}\times e^{x^{2}}+3)$$
これで終了!これを微分方程式の一般解と言い、xとyの組が分かっていれば、代入して特殊解が求まります。
初めて見ると厄介ですがすぐ慣れます。
運動方程式を微分方程式の形で記述してみます
運動方程式 ma=F を微分方程式で記述しましょう。
加速度aは速度vの微小時間の変化を表し、速度vは変位xの微小時間の変化を表すのでした。
ですから、v=dx/dtと書けます。
また、 a=dv/dt ;すなわち加速度αは変位xを二度微分したものであると言えます。
これを二階微分と言い、d^2x/dt^2=αと記述します。これを運動方程式に代入すると、
m (d^2x/dt ^2)=F となります。この表記は今後頻出するので、要チェックです。
さあ、微分方程式のキソを学んで理系科目を繋げようpart(1)のトリ、実際に
雨粒の落下運動を微分方程式で解いていく
重力をg、雨粒の質量m、空気抵抗の比例定数をkとおきます。
学校では”ma=mg-kv”と習いますが、以下のように微分方程式で記述していきます。
因みに、αをd^2x/dt^2としていないのは、右辺にvが有り、v=の形にしやすい為です。
α=dv/dtとして置けば、一階微分方程式で済むメリットもあります。

一般解と初期条件
さて流れはつかめましたか?最後に一般解としてv−mg/k=-(ec)(e-kt/m) が現れました。
ここで、t=0(s)の時v=0(m/s)であるとして、一般解にそれぞれ代入します。
(これを初期条件と言い、代入してできた式を特殊解と言います。
この様に初期条件を変える事によって、いろいろな状態でもvを求めることができます。)
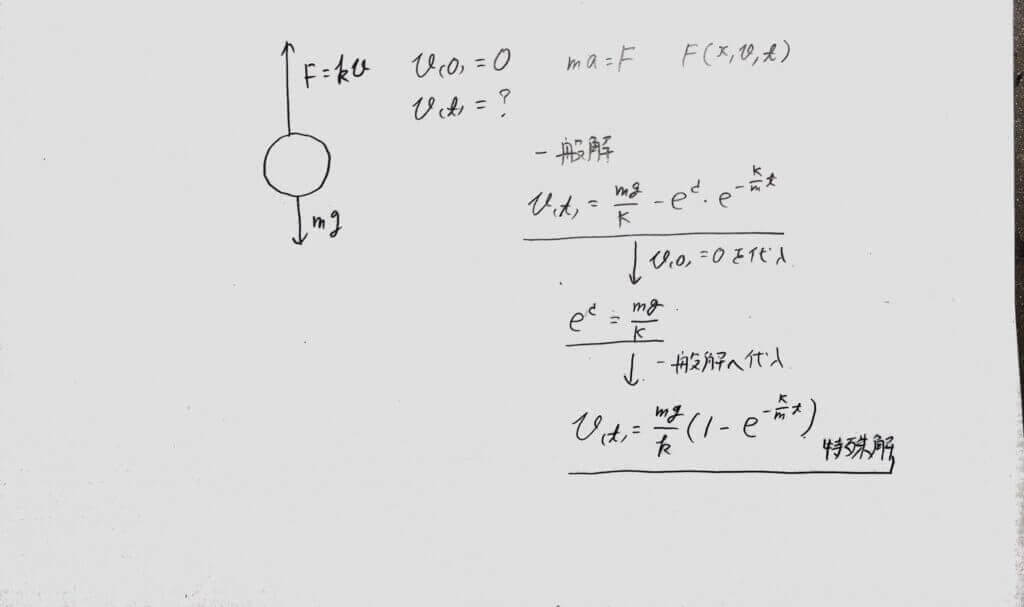
$$特殊解は、V(t)=\frac{mg}{k}(1-e^{\frac{-k}{m}t})$$
特殊解に任意の時間tを代入すると・・・
このようにして求まった特殊解の式の”t”=timeに好きな時間(落下開始からの経過時間)を代入することで、その時の雨粒の速度が求められるようになります!
さらに、時間について極限をとるlim(t→∞)と、mg/kになります。
これは速度がmg/kに収束する(終端速度)、言いかえれば、どんなに長い時間落下しても『mg/k以上の速度に成らない』という事です。
そりゃそうです!雨粒が幾らでも速くなったら雨の日は弾丸が降って来る様なものです!
外も歩けない、車は穴だらけ、屋根も突き破り生活できません。空気抵抗って有り難いですね。
どうでしたか?今日の微分方程式の解法は色々なことに応用できます。
part2で紹介したいと思いますが、具体的には、化学の反応速度論や半減期、物理範囲に至っては紹介しきれません!
そもそもニュートンは物理現象を解くために微分積分学を確立したと言っても過言ではないのです。
微積物理で行くのか高校の教科書通り微積不使用で入試を乗り切るかの論争がありますが、
筆者は理解は微分積分で、入試は基本的に微積不使用でいいと思います。
ただし、一部の大学(特に京大)は微分方程式が好きな様で、数学はもちろん、化学でも微分方程式を解く事を前提とした問題を出してくることがあります。
逆に言えば、しっかりこの記事やこれからの微分方程式の連載を読んで、自分で計算して、過去問を解けば難化した年の京大レベルでも(=ほぼ日本の大学受験何処でも)それ程苦労はしないはずです。
>>「力学が【苦手な人〜最難関大レベル】までの解説記事まとめ!」<<
今日もお読みいただき有難うございました!
よく復習しておいて下さい!(実際手を動かして)
次回もお楽しみに。

