第一宇宙速度の意味と求め方がわかる!~万有引力と円運動~

「万有引力・ケプラー則・宇宙速度」講座(第一宇宙速度）

このシリーズでは、高校物理:力学の最後で習う万有引力の法則・ケプラーの3法則・そして宇宙速度について解説していきます。

宇宙速度には三つの種類がありまが、今回はそのうちの第一宇宙速度について扱います。

第一宇宙速度とは？その意味と求め方

まずはじめに、高度hで地球を周回する運動について考えていきます。

地球を周回する円運動

例えばものすごい速さでボールを地面に水平（高度はh）で投げたとします。

ある一定の条件(速度)未満ならば、当然そのうち地面に落下します。

しかしながら、この「一定の条件」でボールを投げると、空気抵抗などを考えない理想的kな状況では永遠に地球を周り続けます。

＜図１＞をみて下さい。ボールが回り続ける様子です。これはまさに、円運動です

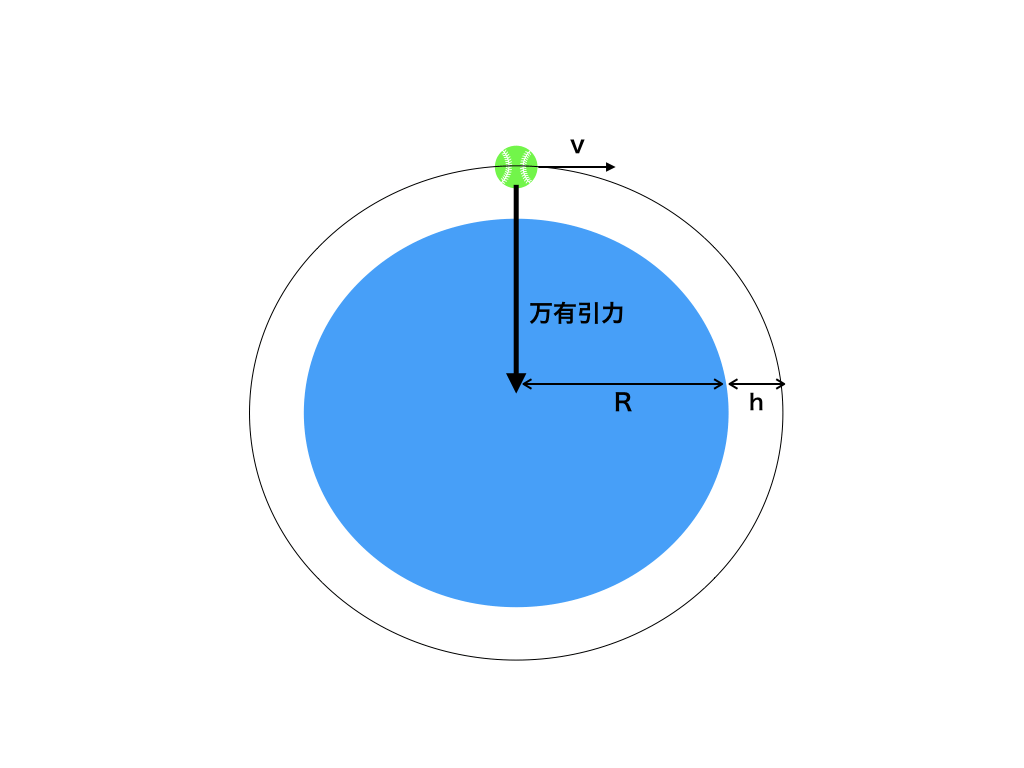
円運動については、単振動の記事の序盤で詳しく説明しています。→「これでわかる！単振動（１）」

上の記事では、角速度ω（rad/s）で解説していますがこの記事では

$$v=rω 、a=rω^{2}=\frac {v^{2}}{r}$$という関係があるので、

$$a=rω^{2}=\frac {v^{2}}{r}$$　と読み替えてください。

円運動であるということは、運動方程式が書けますね。

万有引力を向心力とする円運動

ここでは、向心力（円運動の中心に向かって常に働く力：これがないと、ボールは円の軌道から離れて真っ直ぐ進んでしまう）を『万有引力』として、運動方程式を立てていきます。

※万有引力：すべてのものがお互いに引き合う力の事。

以下に出てくる文字の意味は次のとおりです。（m：ボールの質量、M：地球の質量、R：地球の半径、h：ボールの高度、V：ボールの接線方向の速度、G：万有引力定数）

運動方程式　ma=F のFが万有引力、aが向心加速度、です。

ここで、図1より半径R+h の円運動をしているので、

$$a=\frac {v^{2}}{(R+h)}$$

$$F=G\frac {Mm}{( R+h)^{2}}$$

より、二式をma=Fに代入して

$$m\frac {v^{2}}{(R+h) }=G\frac {Mm}{(R+h)^{2}} $$

がこの円運動の運動方程式になります。この式をvについて解くと、

$$v^{2}=G\frac {M}{R+h}$$

$$v=\sqrt {\frac {GM}{R+h}}$$

従って、初速度vが上の条件を満たしていれば、地球上を周回し続けます。

第一宇宙速度の値を計算する

では第一宇宙速度の解説と計算に入っていきます。

第一宇宙速度は、地面（海面）スレスレの高度で地球を周り続ける（地上に落下しない）ために必要な初速度のことです。すなわち、先ほど計算したvを使って、

$$v=\sqrt {\frac {GM}{R+h}}$$

の式のh（高度）が０の時です。

従って、hに０を代入すると第一宇宙速度v1は、

$$v1=\sqrt {\frac {GM}{R+0}}$$

$$v1=\sqrt {\frac {GM}{R}}$$

ここで実際に、$$v=\sqrt {\frac {GM}{R}}$$に値を代入して見ます。

万有引力定数:G＝6.7×10^-11（m³)/(s²×Kg)

地球の半径R=6400× 10³(m),

地球の質量M=6× 10²⁴ (Kg)

とすると、(分かりやすい様にかなりきれいな数字にしています。実際の試験では、文字のまま出題されるか、必要ならば数値が与えられるのでそれに従ってください。)

これらの数値を$$v_{1}=\sqrt {\frac {GM}{R}}$$

に代入して、$$v_{1}=\sqrt {\frac {6.7× 10^{-11}×6×10^{24}}{6.4×10^{6}}}$$

$$v_{1}=\sqrt {\frac {6.7×6×10^{7}}{6.4}}$$

$$≒\sqrt {6.28× 10^{7}}≒7.9×10^{3}(m/s)$$

従って、大雑把な計算ですが第一宇宙速度は7.9(km/s)と計算できることがわかります。

次に、重力と万有引力の関係を使って宇宙速度を求める方法を見ていきます。

重力＝万有引力？第一宇宙速度のもう一つの導出法

地上から見ると地球は自転しているので、遠心力が働いているように考えることができます。

つまり、重力(mg:gは重力加速度)＝万有引力ー遠心力となるのですが、

高校の範囲では遠心力を無視して考えます。(万有引力に比べて小さ過ぎるため)

そこで、地表付近では以下の式が近似的に成り立ちます。

$$mg=G\frac {Mm}{(R+0) ^{2}}$$

この式より、万有引力定数Gと重力加速度gは

$$g＝G\frac {M}{(R) ^{2}}$$

このように表すことができます。

$$g=\frac {GM}{R^{2}}⇔ gR=\frac {GM}{R}より、$$

$$ここで、v_{1}=\sqrt {\frac {GM}{R}}に上の式を$$

変形して代入すると

$$v_{1}=\sqrt {gR}$$

g(重力加速度）を9.8(m/s²)、R（地球の半径）を6.4× 10⁶(m)として、

$$\begin{aligned}v_{1}=\sqrt {9.8×6.4× 10^{6}}\\
=\sqrt {6272000}0\end{aligned}$$

これを計算すると、第一宇宙速度v1≒7.92× 10³(m/s）

よって、こちらの方法でも第一宇宙速度v1=7.9(km/s)と導出できました。

第一宇宙速度のまとめと次回(第2宇宙速度)他

今回のまとめ

・第一宇宙速度とは、高度がほぼ０、すなわち地面や水面スレスレを理想的な状態で周回し続けるために必要な初速度のことです。

・万有引力を向心力とした円運動を利用して宇宙速度を求めさせる問題は頻出なので何度も繰り返しとく

・万有引力≒mg（重力）を利用しても第一宇宙速度を求めることが出来ます。

・また、問題によっては万有引力の式から重力加速度を導出させる事もあるので、

今回の式変形は自由自在に出来るようになることが大切です。

内容が多かったので、初めて勉強する人は大変だったかもしれません。

一回読んで終わりではなく、何度も繰り返し読んで、次に問題集などで実際に計算してみて下さい！

次回は、今回紹介し切れなかった第二宇宙速度を中心に解説していきます。

第二宇宙速度とケプラーの3法則を読む

続編出来ました！

第一回:今ココ

第二回:「第二宇宙速度と万有引力による位置エネルギーが"負"になる理由」を読む。

第三回:「ケプラーの３法則を徹底解説！(万有引力との融合問題付き)」を読む。