複素数平面シリーズ第6回:回転の応用、なす角+α
<この記事の内容>:これまでの複素数平面シリーズで扱ってきた『極形式』・『回転』・『図形』などを使用しながら、直線のなす角や直交する条件・共線条件を問う問題の解法・解説をします。
<これまでの復習>:「複素数平面の基礎:(1)極形式と直交形式」「(2)複素数平面での積と商・回転」
(記事の最後に総まとめを作ってあります。必要に応じてぜひご利用ください。)
目次(タップした所へ飛びます)
回転の復習/応用と二直線のなす角
本題の二直線のなす角の準備として、「複素数平面(二):極形式の積と商」の復習 +応用を解説します。
複素平面での回転の復習
複素数平面上の点は、
・z=α +βiのようにあらわす『直交形式』と、
・原点からの距離、および偏角argzであらわす『極形式』が存在しました。
さらに、これらの点を“原点を中心として”回転させ、また拡大/縮小させたい場合には、次のような式を使う事で点の移動先が分かるのでした。
※点A(α +βi)を原点を中心にr倍し、角\(\theta\)だけ反時計回りに回転させた先の点Bは、
$$B=A\times r(\cos \theta + i\sin \theta$$
で求めることができる。
回転(原点が中心ではない場合)への応用
ここから少しだけ応用に入ります。
以下の図のような、回転の中心が原点ではない(ここでは点C)ときには、先ほどの式\(B=A\times r(\cos \theta + i\sin \theta)\)をそのまま使用することはできません。
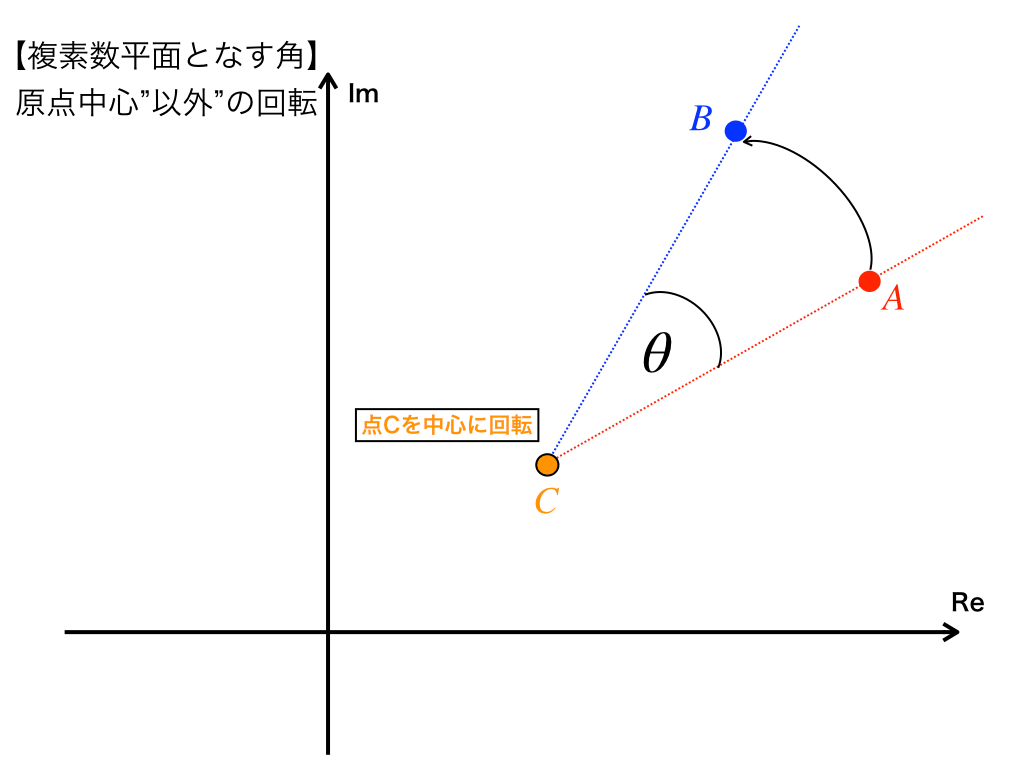
<図1>
そこで、一旦《点Cを原点までずらす》と言う方法を取ります。
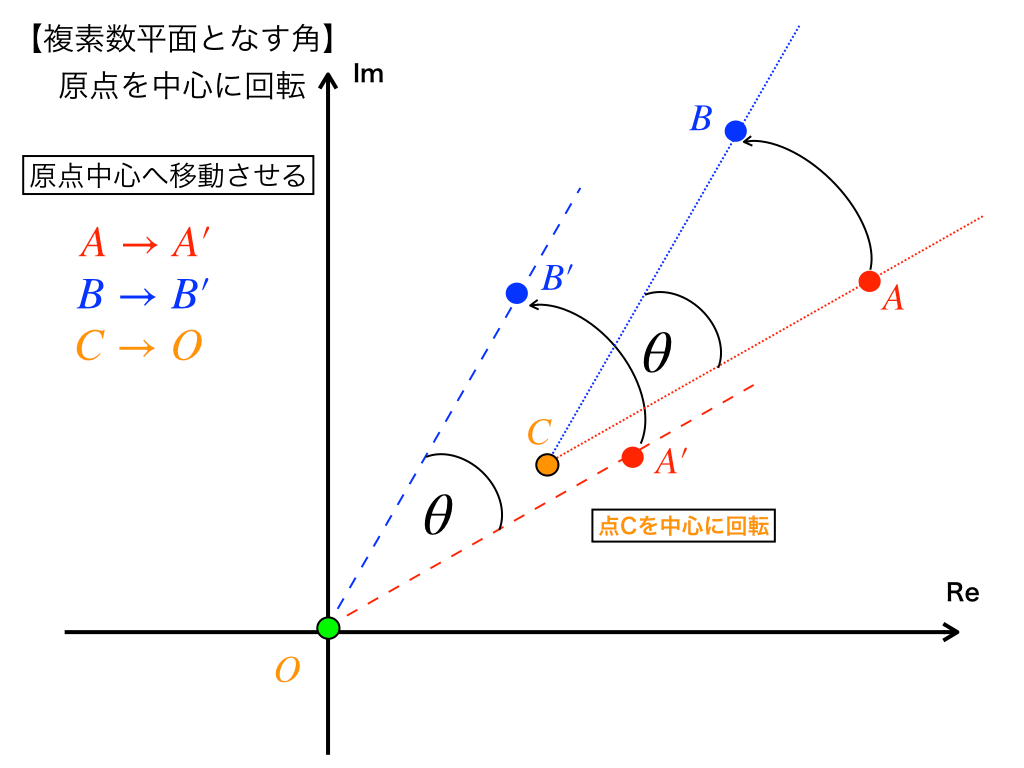
<図1-2>
すると上の図のように点Aは点A‘、点Cは点O、移動先:点B→点B’となります。
これは二次関数のグラフを平行移動させるときに似ています。
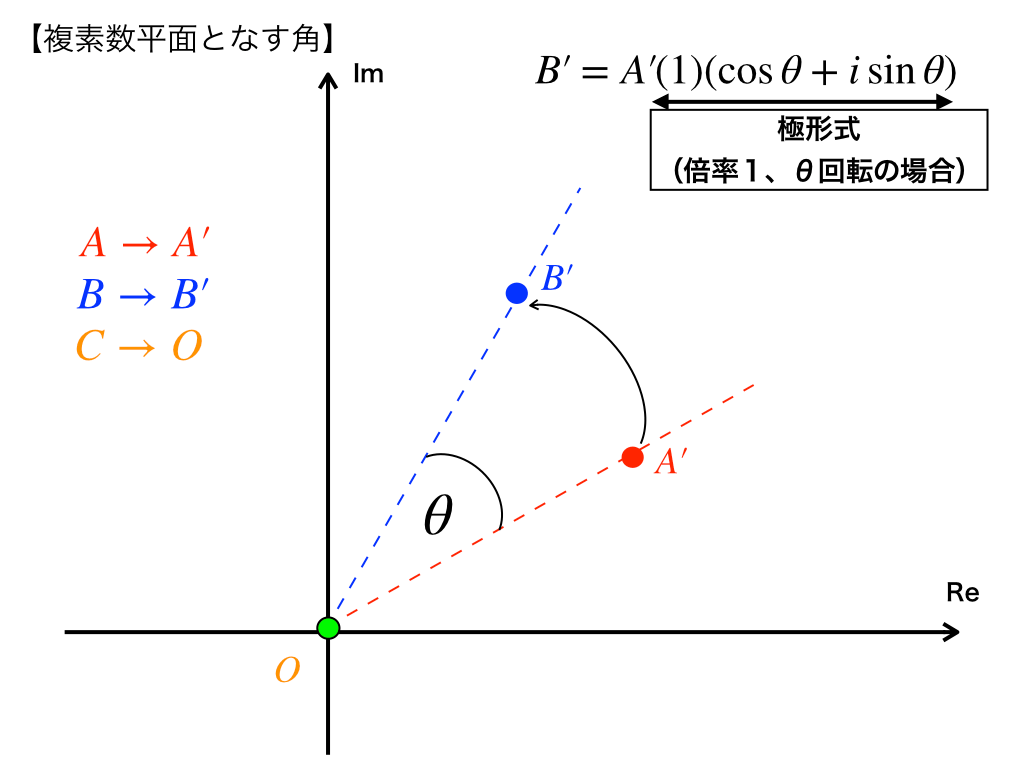
<図1-3>
図1-3において\(B‘=A’\times r(\cos \theta + i\sin \theta)\)が成り立つので、あとはこれを先ほど図1-2でずらした分だけ戻すと、
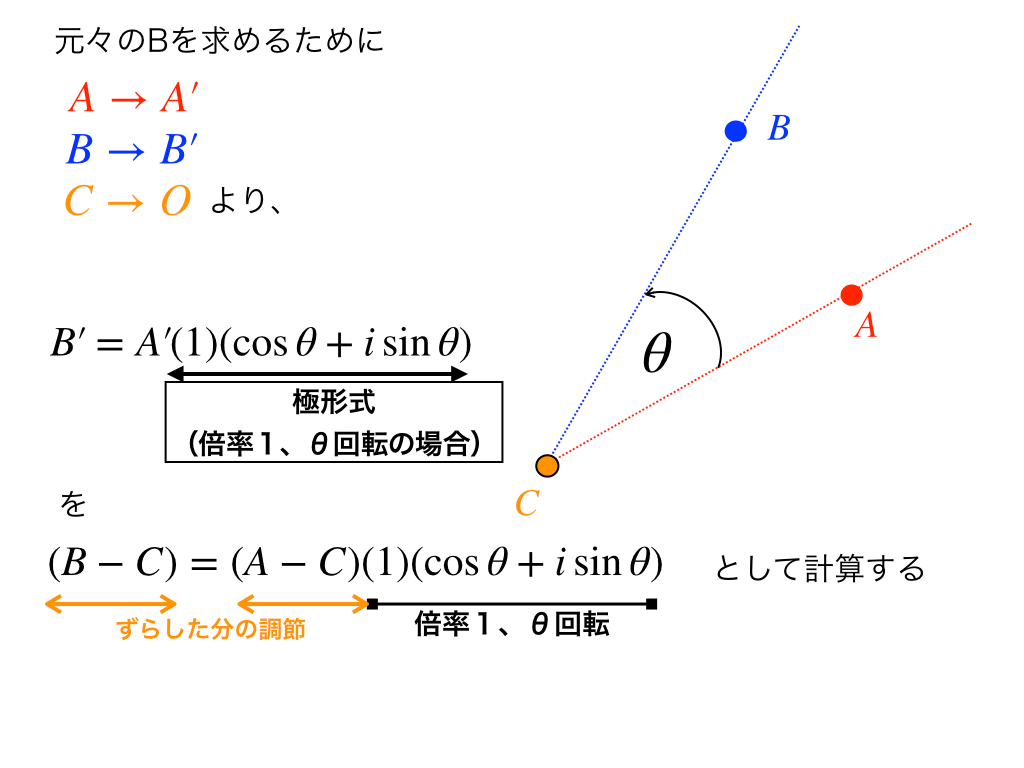
<図1-4>
$$(B-C)=(A-C)(1)(\cos \theta +i\sin \theta)$$
この様に、求めたい点Bが計算できるようになりました。
定着用:応用例題
ここまでは文字だけで紹介して来たので、まだしっくり来ない人もいるかと思います。
例題を用意したので、これを解きながら手順を確認していきましょう。
例題1:以下の図のように、複素数平面上での点A(3,2)を、
点C(1,1)を中心として反時計回りに\(\frac{\pi}{6}(rad)\)回転させ、
AC間のキョリを\(2倍\)にした時の点をBとする。
この時の点Bを直交座標で表せ。
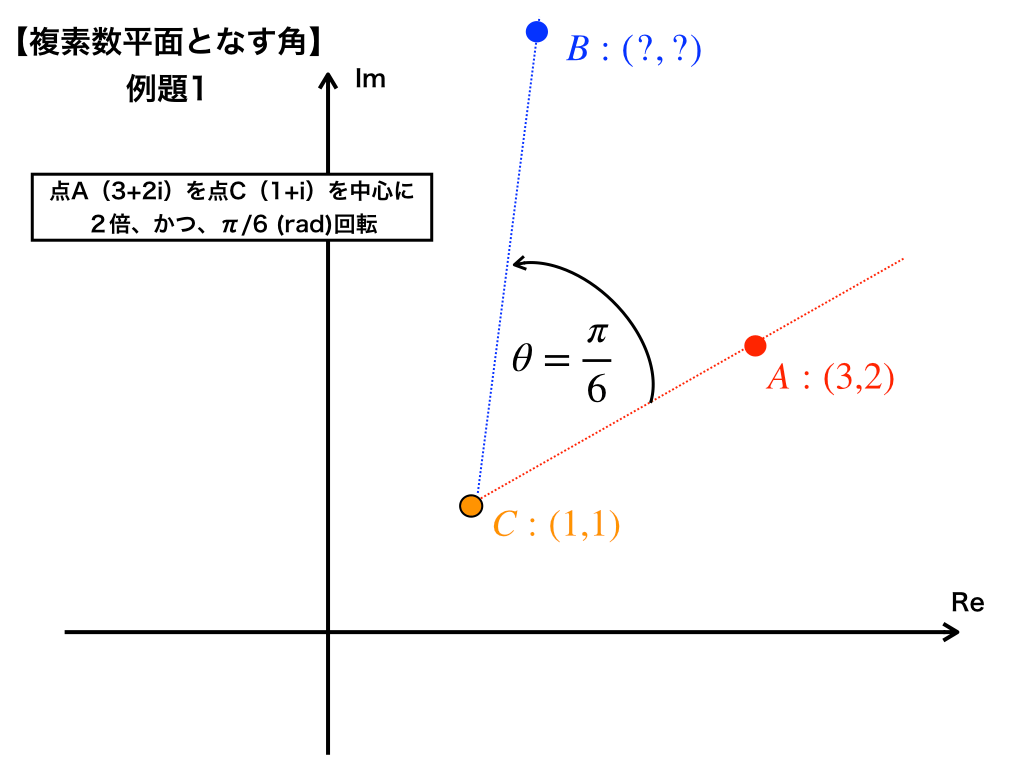
<例題1>
定着例題の回答・解説
とにかく、\((B-C)=(A-C)(1)(\cos \theta +i\sin \theta)\)の式を利用します。
まず、点Cを代入して
$${B-(1+i)}=r(\cos \theta +i\sin \theta){A-(1+i)}$$
問題では\(\frac{\pi}{6}\)回転させて2倍した点を求めるように指示されているので、
点Aと、θ=π/6、r=2をそれぞれ代入すると、
$${B-(1+i)}=2(\cos \frac{\pi}{6} +i\sin \frac{\pi}{6}){3+2i-(1+i)}$$
後はこれを計算していくと、\(B=2\sqrt{3}+(\sqrt{3}+3)i\)と求まり、直交座標で表すと:\(点B(2\sqrt{3},(\sqrt{3}+3))\)・・・(答)
極形式によるなす角の求め方
ここまで点の回転について学んで来ましたが、少し見方を変えます。すなわち、

上の図では点Aから点Bへの回転を考え、$$(B-C)=(A-C)(1)(\cos \theta +i\sin \theta)$$と言う式を導きました。
逆に、直線ACと直線BCのなす角は\(\theta \)であるので、上の式の両辺を( \((A-C)\)≠0のもとで)割ってあげると、$$\frac{(B-C)}{(A-C)}=(\cos \theta +i\sin \theta)$$となります。(下の図参照)
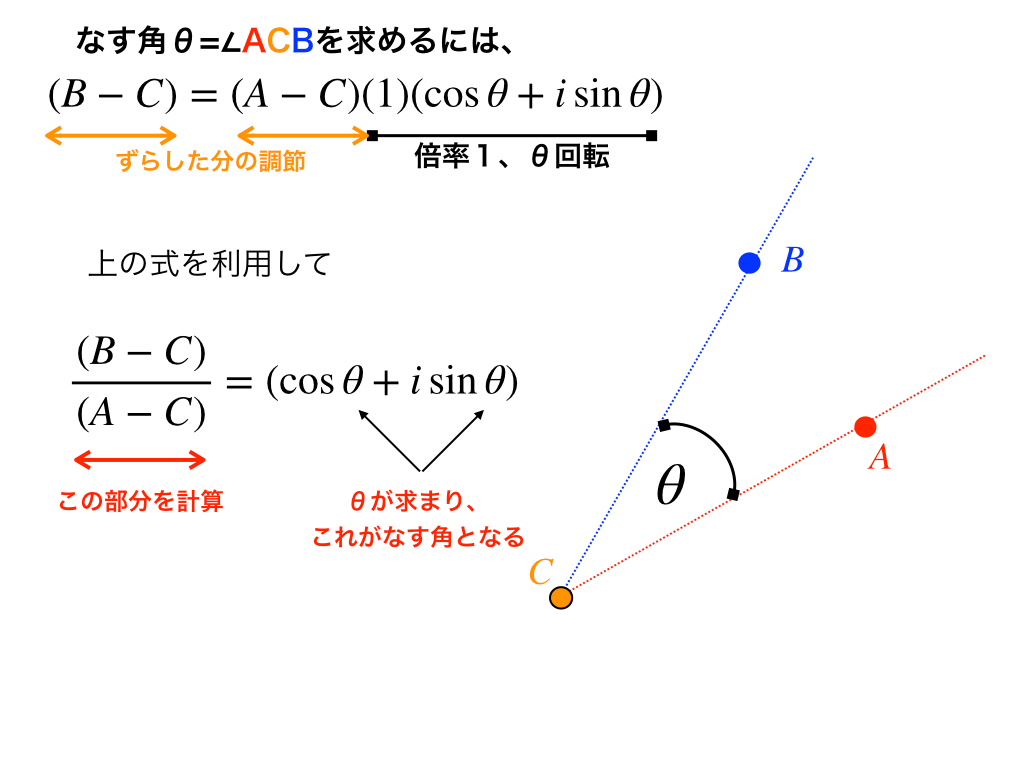
つまり、(左辺)を計算する事で\(なす角\theta\)を求めることができるのです。
具体的な手順と練習問題
これも練習問題を通して、実際に確認しておきます。
(例題2):複素数平面上に、点A(1+2i),点B(-2-4i),点C(3+6i)の3点がある。
ここで、角ACBの大きさ(直線ACと直線BCのなす角)を求めよ。
<解答2>:上の図と式の通りに計算していくだけです。
まず、\(\frac{BC}{AC}=r(cos \theta +i\sin \theta)\)
の$$(左辺)=\frac{(-2-4i)-(3+6i)}{(1+2i)-(3+6i)}=\frac{5(1+2i)}{2(1+2i)}=\frac{5}{2}$$
となって、実数のみになりました。つまり、isinθ の部分が0であることからθ=π(rad)・・・(答)であることが分かります。
このように、複素数の虚数部分がなくなって実数だけ→なす角が0(rad)かπ(rad)→3点が一直線上に並んでいる。
ということは非常に大切(以下で紹介する”共線条件”)なので、覚えておくようにしましょう。
なす角から直交/共線条件への応用
ここまでの『原点以外を中心とする回転→なす角の求め方』まで分かれば、
次はこれを上手く利用して《二つの直線がどの様な関係にあるのか》を調べることができるようになります。
二直線の直交条件
共線条件と共に頻出である、直交条件について見ていきます。
直交条件
二直線が「直交している条件」=交点と2つの直線上のそれぞれの点(下図ではA,B)を考えた時、なす角がπ/2(rad)か、3π/2(rad)であること。
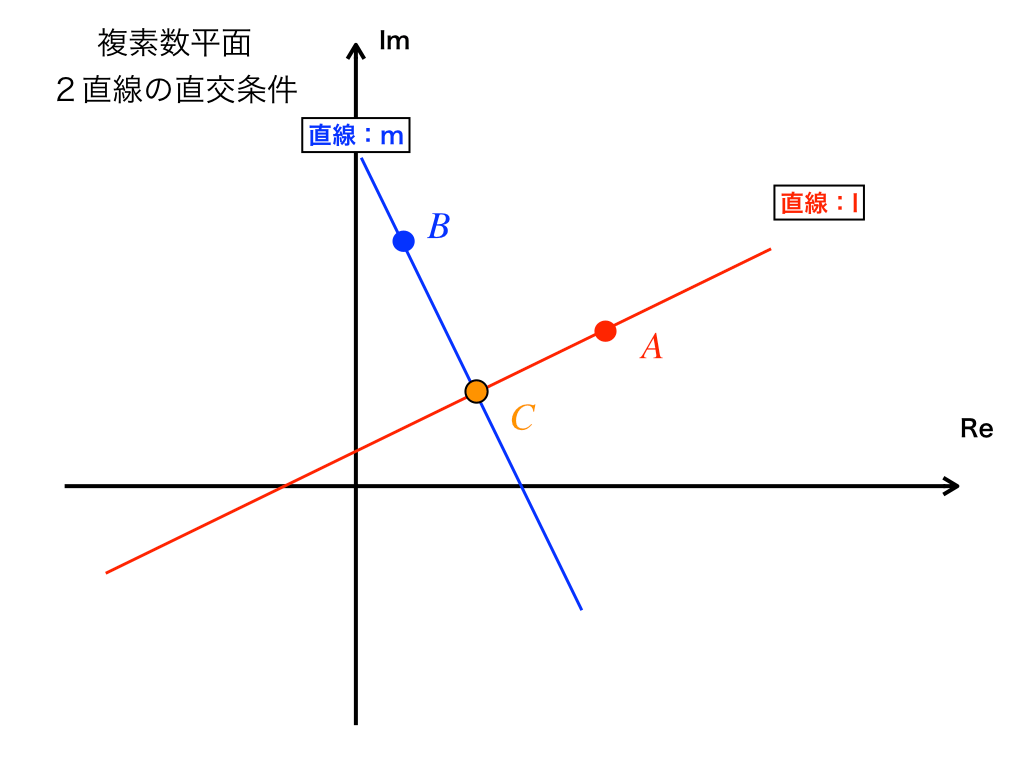
(直交条件の問題を追記中)
共線条件とベクトル
《二直線が共線である条件=2直線上の3点が同一直線上に並ぶ=すなわち、なす角がπ(rad)か0(rad)であること」》
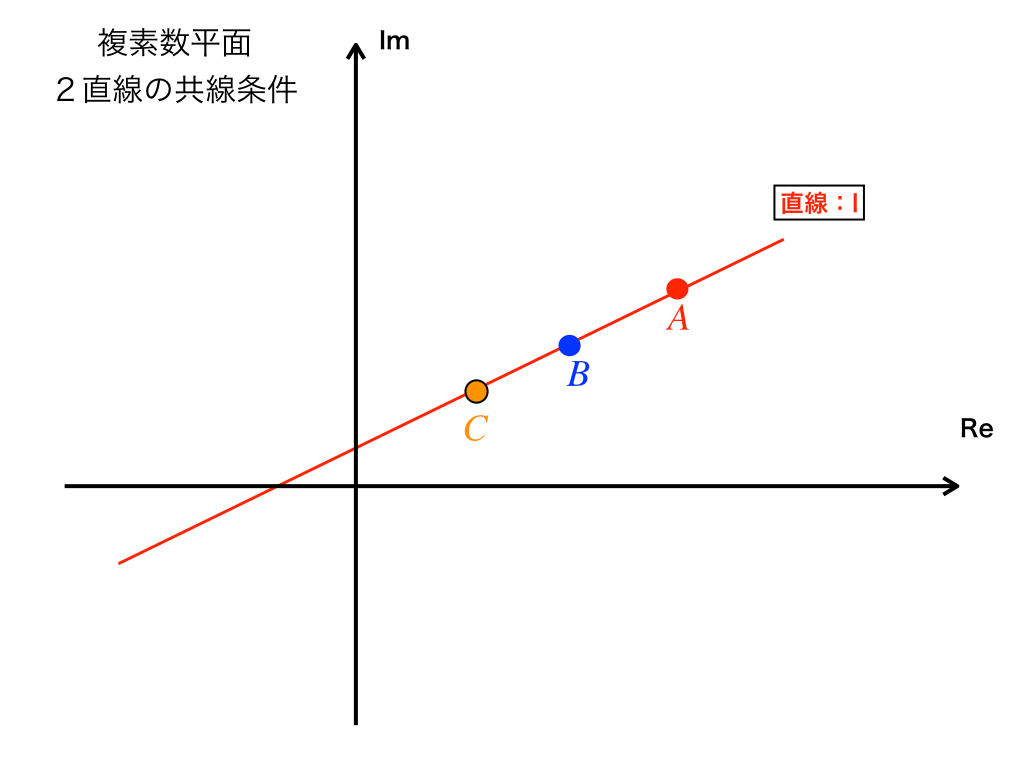
共線条件は、すでに先ほどの例題2で紹介しているので一旦省略します。
が、”ベクトル”での共線条件の解説記事:「平面/空間ベクトルと共線/共面条件と問題の解き方」を参考として載せておきます。
なす角と関連分野まとめ
今回見て来たように、$$(B-C)=(A-C)(1)(\cos \theta +i\sin \theta)$$←この回転の式を上手く応用することで、図形の問題がカンタンに解けてしまうことが多くあります。
この様に、数式で図形の問題を処理するためにも、
・ベクトル:「数学Bベクトルを0から解説!記事一覧」
・三角関数:「三角比/三角関数とその公式などのまとめ」
・複素数平面:「複素数平面の解法・解説記事まとめ」
・図形と方程式:「図形と方程式の解法解説まとめページ」
の四つの分野を、問題に応じて使いこなせるようになりましょう!
複素数平面の解説シリーズ一覧と続編へ
前回:「複素数平面(五):アポロニウスの円」
次回:「(作成中)第七回:条件を満たして動く軌跡」
(現在【複素数平面のまとめページを作成中です】)
作成済みです。2019/07/19。
今回も最後までご覧いただきまして、本当に有難うございました。
当サイト:「スマナビング!」では、読者の皆さんのご意見・ご感想や、記事リクエストの募集を行っています。コメント欄までお寄せください。
また、お役に立ちましたら、B!やSNSでシェアをしていただけると大変励みになります。
・その他のお問い合わせ/ご依頼に付きましては、お問い合わせページよりご連絡下さい。

