複素数平面入門:第一回
<この記事の内容>:数学Ⅲの複素数平面の解説シリーズの第1回として、数2範囲の複素数の復習から、直交形式(座標)と極形式(極座標)の意味と変換の詳しい手順、さらに複素数をかけることによる図形的な意味の基礎まで解説しています。
<関連記事>:「ド・モアブルの定理とその応用」と、
続編:「複素数平面第2回:極形式の積と商をさらに詳しく」(現在続々編を作成中です)
目次(タップした所へ飛びます)
複素数平面とは
これから高校数学3:複素数平面を扱って行きます。内容は、数学2の複素数を発展させたものですが、
少々他の単元と異なった感じがする人が多く、(数学Bのベクトルに近い感覚でしょうか?)得意・不得意が分かれる単元です。
しかし、複素数平面は一度習得して(慣れて)しまうと応用範囲が広く、非常に便利です。
特に”図形問題”にはかなりの威力を発揮します!(これは先述した『ベクトル』と同様に、幾何的に解くことが難しい問題でも計算や式変形で解くことができるからです)
複素数とは(数2の復習から数3へ)
まずはじめにこの項では、数学2で学ぶ複素数のおさらいをしていきます。
数学2の範囲では、
・複素数はZ=a+bi (a、bは実数でiは虚数単位)で表すことができ、特にa=0(つまりZ=bi)のものを純虚数、b=0(同様に、Z=a)のものを実数と呼びこと
・虚数単位iについては、「二乗すれば-1になる想像上の数」で、
・具体的に説明される使用法は、これまで判別式D<0の場合には”解なし”だった二次方程式の解を、iをつかうことで求められると言うことを学びました。
(事前知識):ベクトルと三角関数
この記事の最後でもまとめていますが、複素数平面において『三角関数』と『ベクトル』はある程度自由に使えることが必須になってきます。
数2Bの分野が曖昧な人は、以下の記事を利用して先に復習しておきましょう。
・「三角関数の公式の導き方・覚え方まとめ」「三角関数の基礎!三角比のまとめ」
準備が整ったところで、ここからいよいよ複素数平面とは何かについて、具体的に見ていきましょう。
複素数と座標平面
数学2で習った虚数単位”i”は、二乗するとー1になりました。
今、1にiを二回かけると、ー1になります。次にー1もう一度iを二回かける(二乗する)と1に戻ります。
これを座標上で表すことを考えます。
すなわち、複素数「z=a+bi」を通常の座標を成分表示するときのように、(a、b)として、
・x軸にあたるところをRe(実数の軸=実軸)
・y軸にあたるところをIm(虚数の軸=虚軸)として扱います。
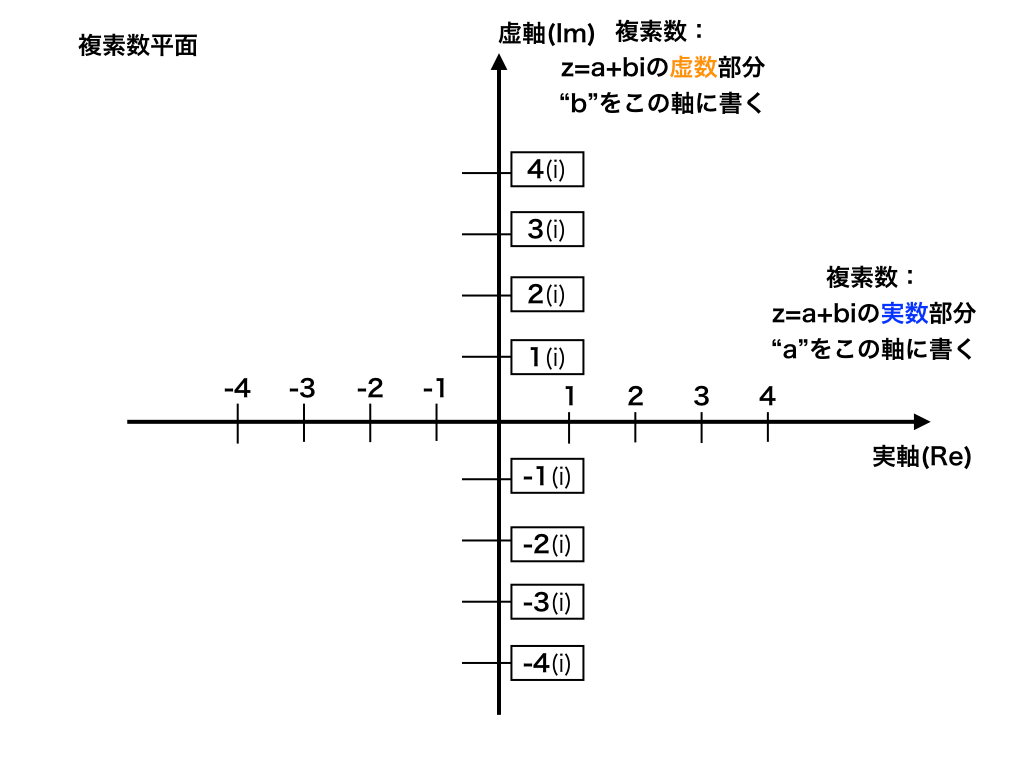
<複素数平面と座標>
初めての人はピンとこないかと思うので、先ほどから例示している、実数1(つまりz=の形で表すと、z=1+0i)を複素数平面上に書き込んでみます。
z=1+0iより、点zは複素数平面上の(1、0)、つまり実軸Re上で原点から”1”正方向へ離れた場所にいます。
これにiを2回かけると、(-1、0)に移動したことがわかります。(詳しく書くと、1×i×i=−1、z=-1+0i)
さらにもう二回iをかけると、(1、0)に戻ってきます。
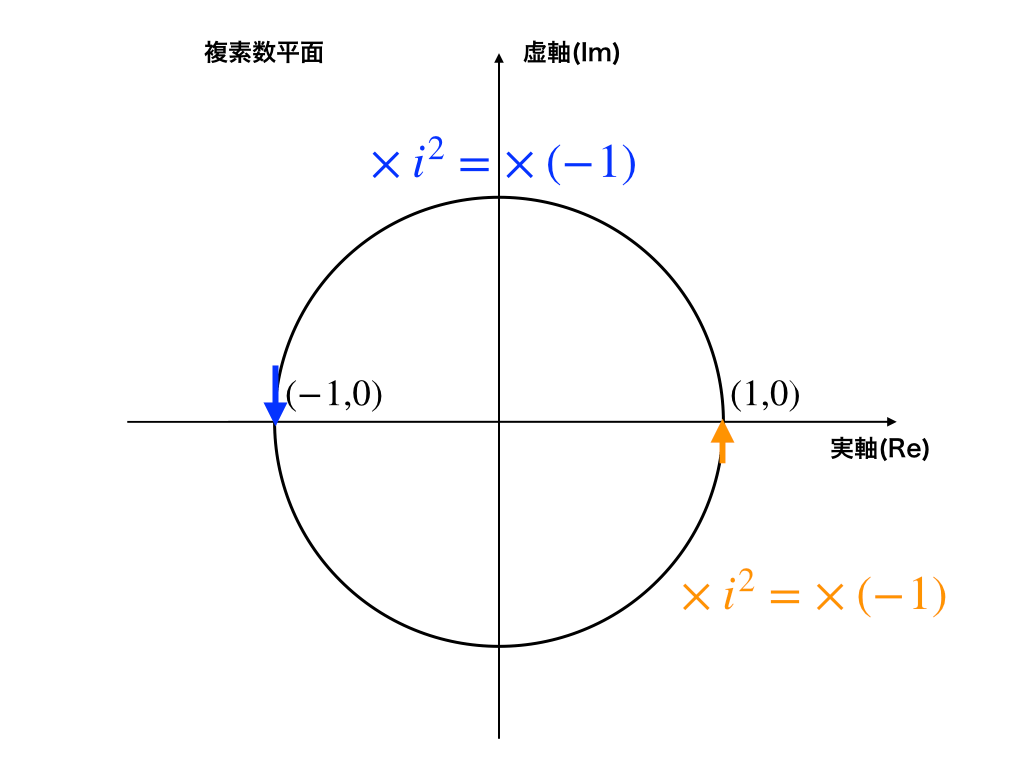
<図1:複素平面の例>
回転と虚数単位i
では、iを1回だけ掛けるとどうなるのでしょうか?
iを4回かけたら元に戻った(360°回転した)事を考えると、90°回転するのが妥当な感じがします。
ここで実験の為、複素数z=3+2iを考えます。
複素数平面上では(3、2)です。zにiを掛けると3iー2=-2+3iとなり、再び複素平面上で考えるとその点は(-2、3)になります。
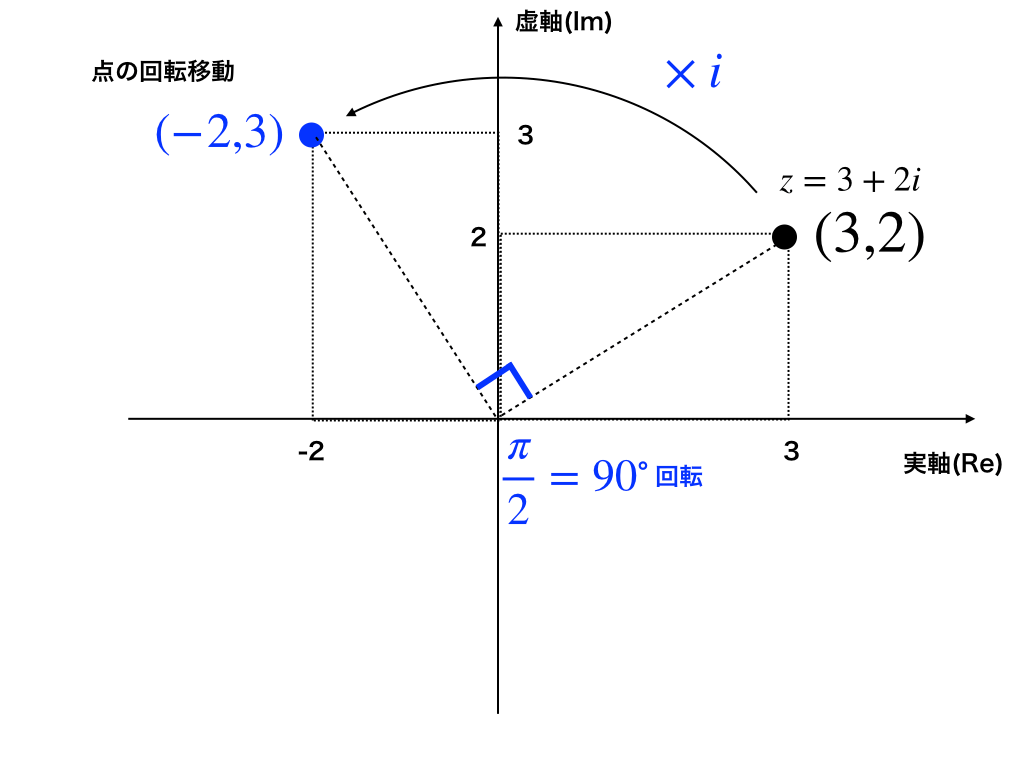
<図2:iを掛ける>
確かに原点を中心に90°回転移動しています。
この様に、「iを掛ける事」は複素数平面上で「原点を中心に90°回転させる」という意味がある事がわかります。
直交座標(形式)から極座標(形式)へ
ここからは、今まで複素数を扱う時に使ってきた直交形式(Z=a+bi)から、極形式と呼ばれるものへ変換して行きます。
これによって、複素数の「図形に強い・回転の計算が容易」と言った性質を引き出すことができます。
極形式とは?
具体的な例を使って身につけていきましょう。
今、Z=1+√3i(z=a+biの形の式を直交形式と呼びます)を直交座標で表すと、(1、√3)となります。
一方で、これを原点からの距離と実軸から反時計回りの角度で表したもの(2、π/3)を「極座標」と言います。
「極座標」を数式に戻すと「極形式」とよばれるものになり、Z=2(cosπ/3+isinπ/3)と表します。
この時の「原点からの距離」のことを絶対値と言い、角度を偏角とよびます。

直交形式を極形式に変換する
上述したように、直交形式だけでは複素数の良さを活かしきれないため、これから説明する方法でまずは極形式に変えていきます。
方法は、三角関数の合成とよく似ています。(参考→三角関数の合成と加法定理)
今回は、図を書いて極形式に変換する方法をとります。
具体的な極形式への変換手順
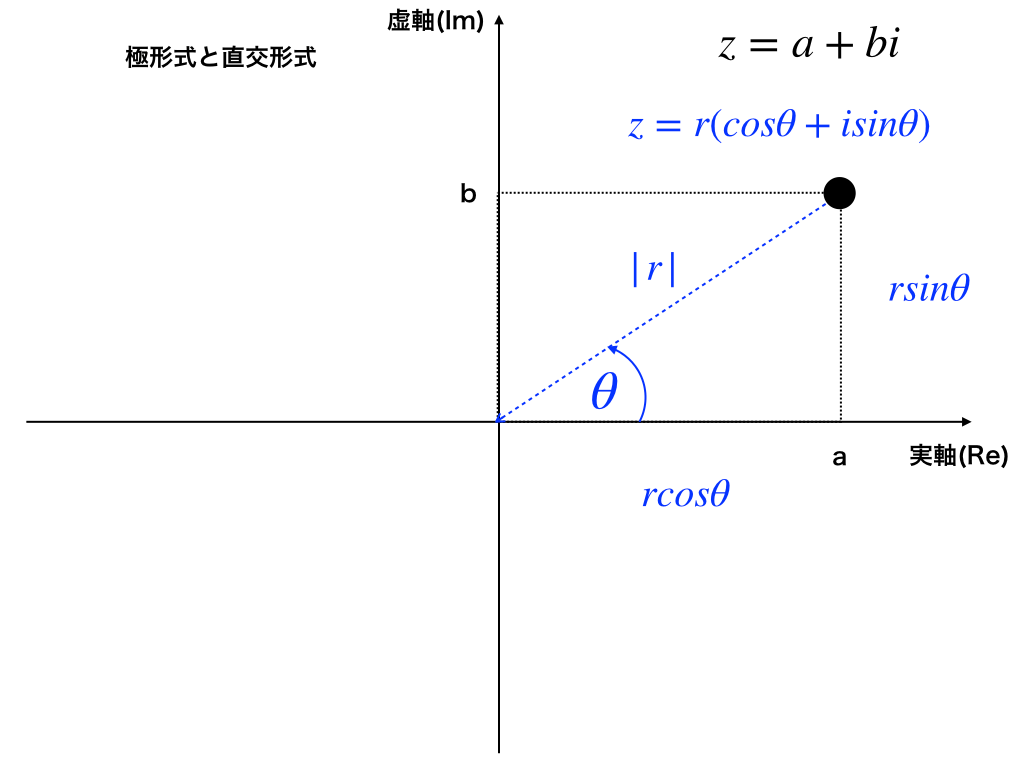
<図3:直交形式から極形式へ>
手順1:Z=a+biのaを複素数平面の実軸(Re軸)上にかく
手順2:bを同様に虚軸(Im軸)上にかく
手順3:三平方の定理を用いて絶対値を求め、その値を極形式のrとする
手順4:実軸からの反時計回りの角度を偏角argθとし、極形式のθに代入する。
→極形式:Z=r(cosθ+isinθ)
$$z_{1}=r_{1}( \cos θ_{1}+i\sin θ_{1}) $$
$$z_{2}=r_{2}(\cos θ_{2}+i\sin θ_{2}) $$
複素平面(1)まとめとベクトル/三角関数の記事
次回は、いよいよこの『極形式』を用いて複素数平面上で任意の点を好きな角度だけ回転させたり、伸縮させる方法と実例、その証明を行なっていきます。
また、繰り返しになりますが、『ベクトル』・『三角関数』の知識が必要になることが多々あるので、時間があるときに、次のまとめページを利用して復習しておきましょう。
次回・および関連記事一覧
予備知識:「ベクトルの解説記事まとめ」「三角関数・三角比の公式の覚え方・導き方」
複素数平面:第一回「今ここです」
複素数平面:第二回「複素数の積/商と回転の関係・伸縮と加法定理」
複素数平面:第三回「外分点・内分点の座標と位置の求め方(複素平面/図形と方程式)」
第四回:「ド・モアブルの定理とその三角関数への応用」
第五回:「複素数平面と軌跡・円の式を解説!」
(2019/06/07更新):「複素数平面の解説記事まとめ」を作成しました。
今回も最後までご覧頂き、有難うございました。
当サイト「スマナビング!」では、読者の皆さんのご意見や、記事のリクエストの募集をコメント欄にて行なっています。
また、お役に立ちましたら、B!やシェアをしていただけると励みになります。
・その他のお問い合わせ/ご依頼に関しましては、お問い合わせページからご連絡下さい。

