運動量と力積・はねかえり係数
<この記事の内容>:高校物理の力学分野において、力学的エネルギーと共に最重要な
・”運動量”と力積の関係から、
・運動量保存則、さらに苦手な人が多い
・『はねかえり係数』まで解説し、
↓
最後に頻出問題を通して理解を定着させます。
<関連する記事>:「力学で困らないための『三角比』・『ベクトル』予習/復習」
【↓↓タップ・クリック可能なもくじ↓↓】
目次(タップした所へ飛びます)
運動量とは
運動量はよく「勢い」に例えられます。以下の定義の通り、早く移動していて質量が大きいものほど運動量は大きくなります。
運動エネルギーとの違い(スカラー量とベクトル量、他)などに注意しながら、上手く両方を利用して問題を解ける様になりましょう。
運動量の定義
運動量p=質量m・速さv
\(\vec{p}=m\vec{v}\)
ベクトル量であることに注意!
力積と仕事の違い
力学的エネルギーは「仕事」\(F\cdot x=W\)
運動量は「力積」\(F\cdot t=I\)
これらは非常にまぎらわしいですが、それぞれの式をよく見てみると「仕事」はどれだけ頑張って力を加えてもその物体が動かない(=xが0)であればW=0となります。
一方で、『力積』の方は仮に物体が動かなくとも力をかけた時間で表されるので、I≠0となります。
運動量保存則
\(m_{1}\vec{v_{1前}}+m_{2}\vec{v_{2前}}+\cdots+m_{n}\vec{v_{n前}}\)
\(=m_{1}\vec{v_{1後}}+\cdots +m_{n後}\vec{v_{n後}}\)
保存則の使い方のコツ
コツは(衝突後の)物体がどちらに移動するかわからない場合が多いので、すべて正方向と一旦仮定しておきます。
微分方程式(応用)による導出
応用レベルですが、「運動方程式から運動量/エネルギー保存則を導出する」で、\(m\vec{a}=\vec{F}\)から、それぞれの保存則を導き出す方法(変数分離形の”微分方程式”を利用します)を紹介しています。
はねかえり係数e
(相対速度の考え方は→「相対速度とモンキーハンティング」で解説)
はね返り係数eは
$$e=-\frac{V_{相手(後)}-V_{観る方(後)}}{V_{相手(前)}-V_{観る方(前)}}$$
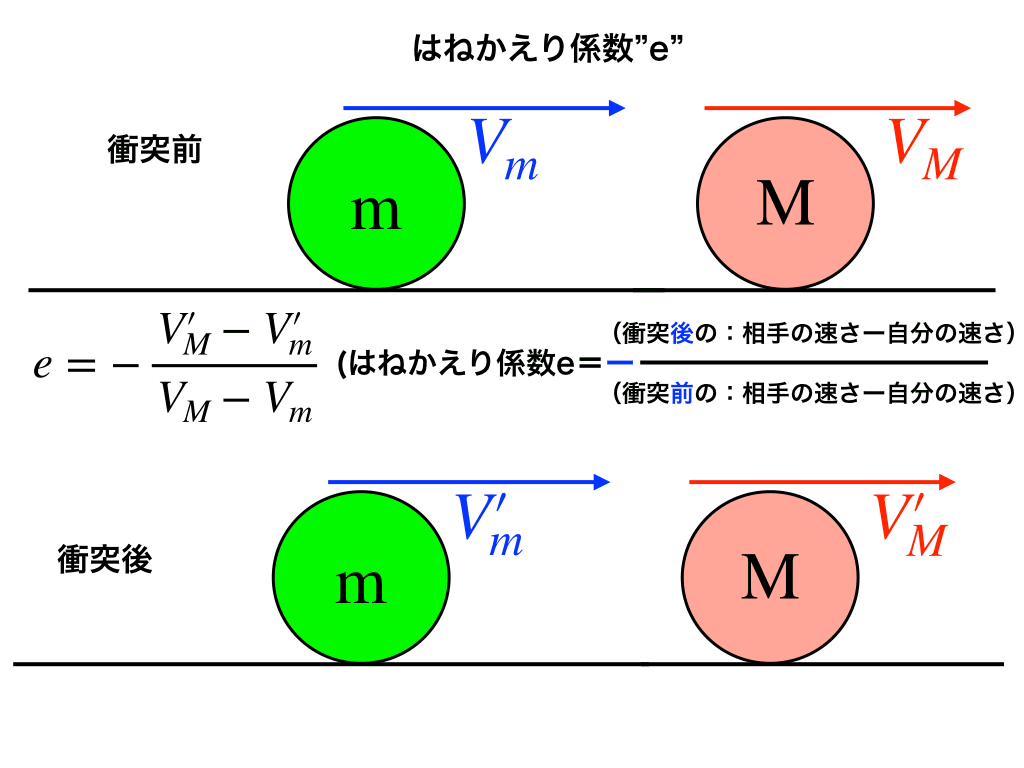
完全弾性衝突
e=1のとき、すなわち分母の相対速度=分子の相対速度の場合を『完全』弾性衝突と呼びます。
この時(のみ)、力学的エネルギー保存則を用いることができます。
非弾性衝突
0<e<1のとき、すなわち分母の相対速度が分子の相対速度より大きい場合を『非弾性衝突』と呼びます。一つ下の『完全』非弾性衝突との違いに注意しましょう。
完全非弾性衝突
e=0のとき、すなわち分子の相対速度が“0”の場合を『完全非弾性衝突』と呼びます。
【分子の相対速度=0】という事は、衝突した二物体が『同じ向きに同じ速さで運動』している→くっ付いている、という状態です。
運動量と力積を用いる問題
ここまでの知識を使って、力積と運動量の分野でよく出題される問題を解いてみましょう。
斜め向きの力積
次の図の様に、球とバットの衝突の問題を見ていきます。
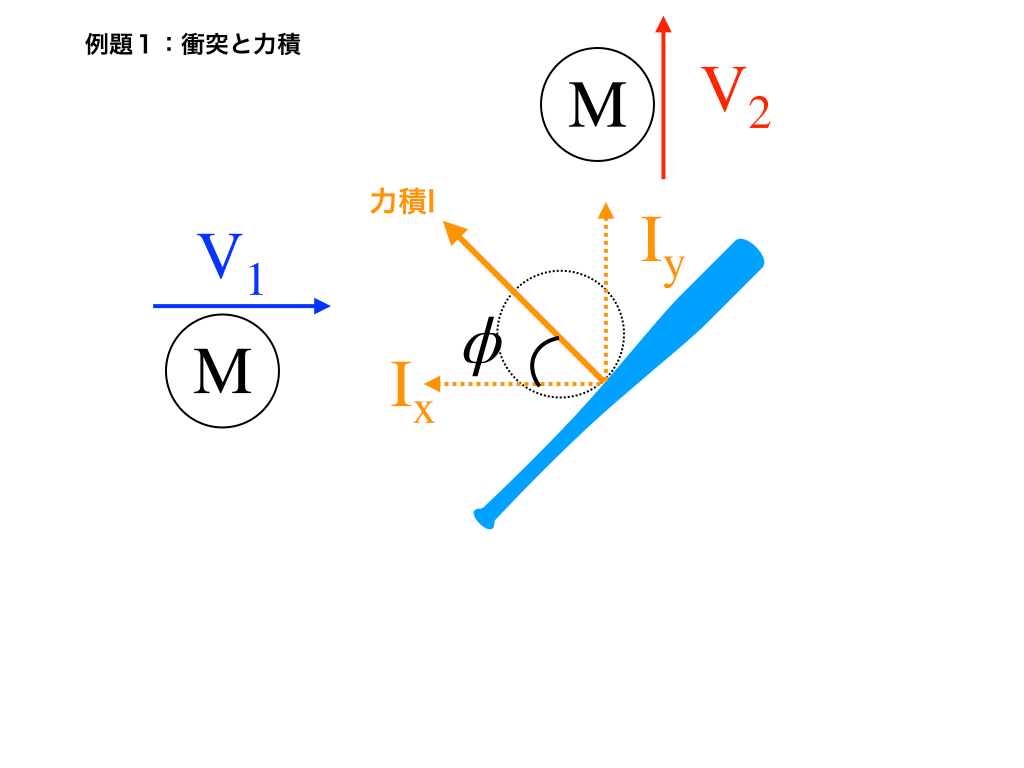
例題1:いま以下の図のように、右向きに速さ\(V_{1}\)で飛んでいる質量Mのボールがバットに衝突し、真上方向に向きを変えて速さ\(V_{2}\)になって進んだ。
この時の力積の大きさと向き(図中の\(\phi(rad)\))を求めよ。
力積とベクトル(解答1)
最も簡単に解く方法は以下のようにベクトルの足し算/引き算を利用することです。
始点を揃えて、矢印の先からもう一方の先へ向かうベクトルがです。
\(I=M\cdot \sqrt{V_{1}^{2}+V_{2}^{2}}\)
向きは、\(\tan\) を用いて
$$\tan\phi=\frac{V_{2}}{V_{1}}$$
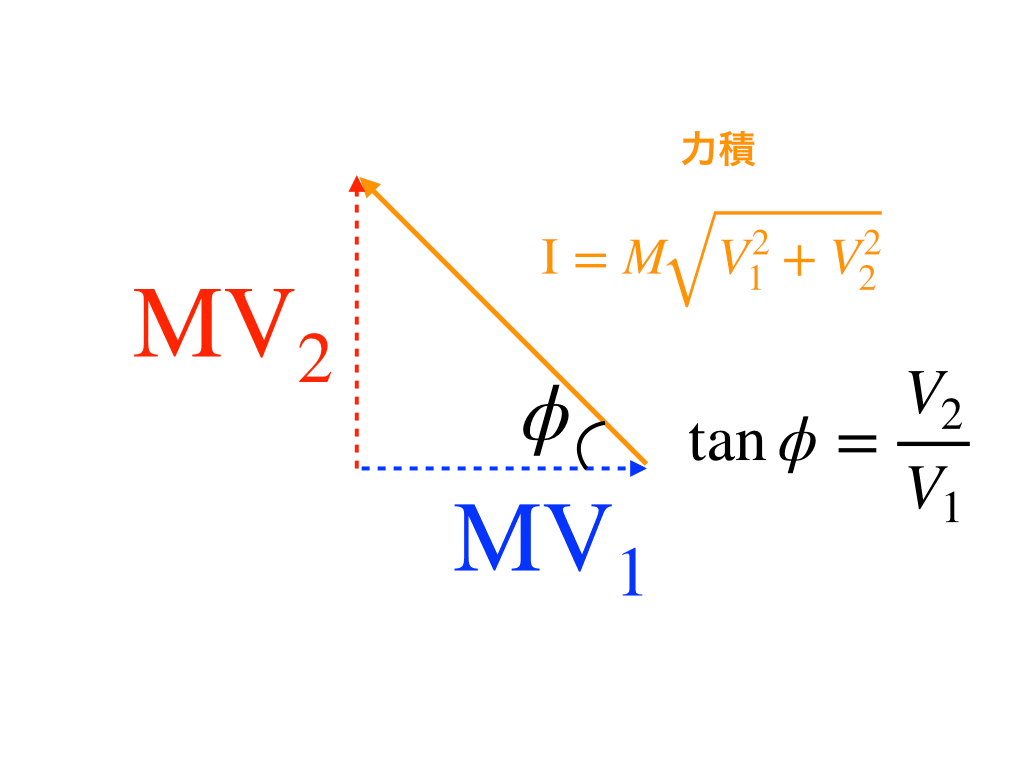
(※:\(MとV_{1}、V_{2}\)にそれぞれ具体的な数値を入れて見るとより上の図が理解しやすくなるはずです。)
例:\(V_{1}=10(m/s)、V_{2}=10\sqrt{3}(m/s)\)M=1(Kg)の場合は
\(力積=20(Ns)で\tan\phi=\sqrt{3}、よって\phi=\pi/3\)
ロケットの問題
次は“相対速度と運動量保存則”をうまく使う問題です。
空気の無い宇宙空間でロケットや人工衛星・探査機が進むために実際に利用されている原理です。
(他にも惑星を使ったスイングバイなどもありますが、ここでは扱いません。)
例題2:いま速さV、質量M+mのスペースシャトルが、(自船から見て)進行方向逆向きに速さvで質量mの燃料を噴射した。(簡単にするためにmの球とする)
噴射後、スペースシャトルの速度がいくらになったのか求めよ。
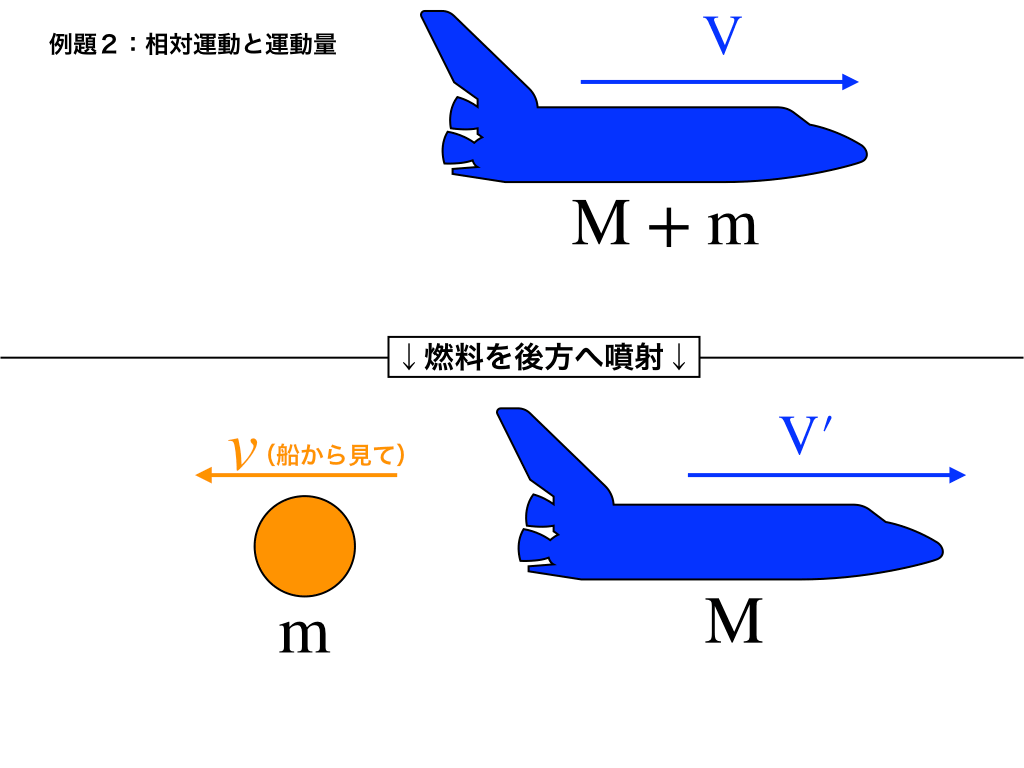
宇宙空間での運動量保存の融合(解答2)
“スペースシャトルから見て”vで噴射しているのでこのvはあくまでも《相対速度》である事に注意が必要です。
外から観測した実際の燃料の速さは、\(v_{実}-V‘=-v_{相}\)であるので\(v_{実}=V’-v\)
運動量保存則より、
(噴射する前の質量・V=噴射後の質量・V’+燃料の質量・v)
(M+m)V=MV’+m(V’-v)
これを解くと、
$$V’=V+\frac{v}{M+m}\cdots (答)$$
結果を見るとVは右向きを正とすると+、M+mも質量なのでプラス、あとはvの大きさ次第でどのくらい速度が増加するかが分かります。
運動量と力積まとめ
運動量や跳ね返り係数などについては、今回紹介した以外にもさまざまな種類の問題があります。
ハイレベルな入試問題では数列の極限などとも融合されるなど、応用問題も豊富なので、今後関連記事(演習問題とコツ)を増やしていく予定です!
関連記事一覧
最後までご覧頂き、有難う御座いました。
「スマナビング!」では、読者の皆さんのご意見・ご感想をコメント欄で募集中です。
snsでシェア、Twitterのフォローをして頂けると励みになります。
・お問い合わせ/ご依頼・その他ご連絡は【運営元ページ】よりお願い致します。

