
領域の基礎:第1回(一次不等式から積による領域まで)
<この記事の内容>:『図形と方程式』での最難関分野の一つである『領域』の第一回目として、一次不等式が表す領域から『連立不等式』や『方程式の積』が表す領域まで詳しく紹介しました。
目次(タップした所へ飛びます)
領域とは
方程式をxy座標上に描くと、例えばy=xであれば(0,0),(1,1),,,,とxの値とyの値が等しい無数の点の集合(=これを直線として描いていました)。
これまでの”方程式”を”不等式”に変化させることで、この直線(や曲線)上の点『以外の無数の点』を集めて、塗り潰したような部分を表すことができます。
これが『領域』の簡単なイメージです。
実際に色々な不等式を使って『領域』の感覚に慣れていきましょう。
一次不等式と領域
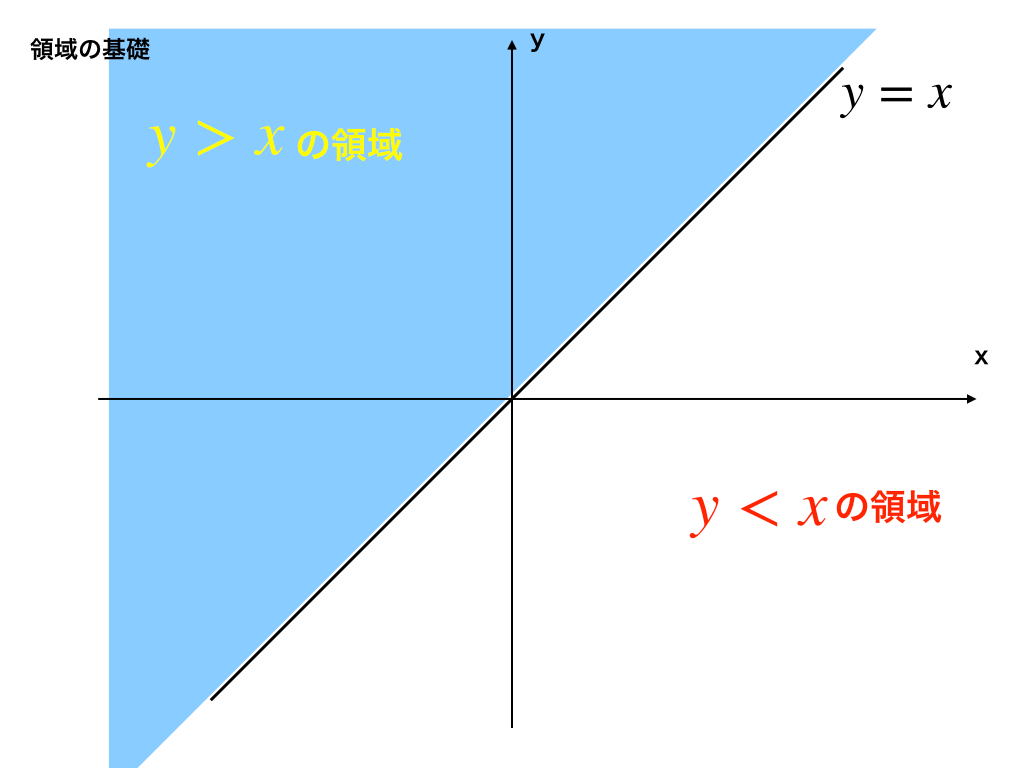
以下のように、\(y=x\)を境にして\(y>x\)は上側の部分・\(y<x\)は下側の部分を表します。
二次不等式と領域
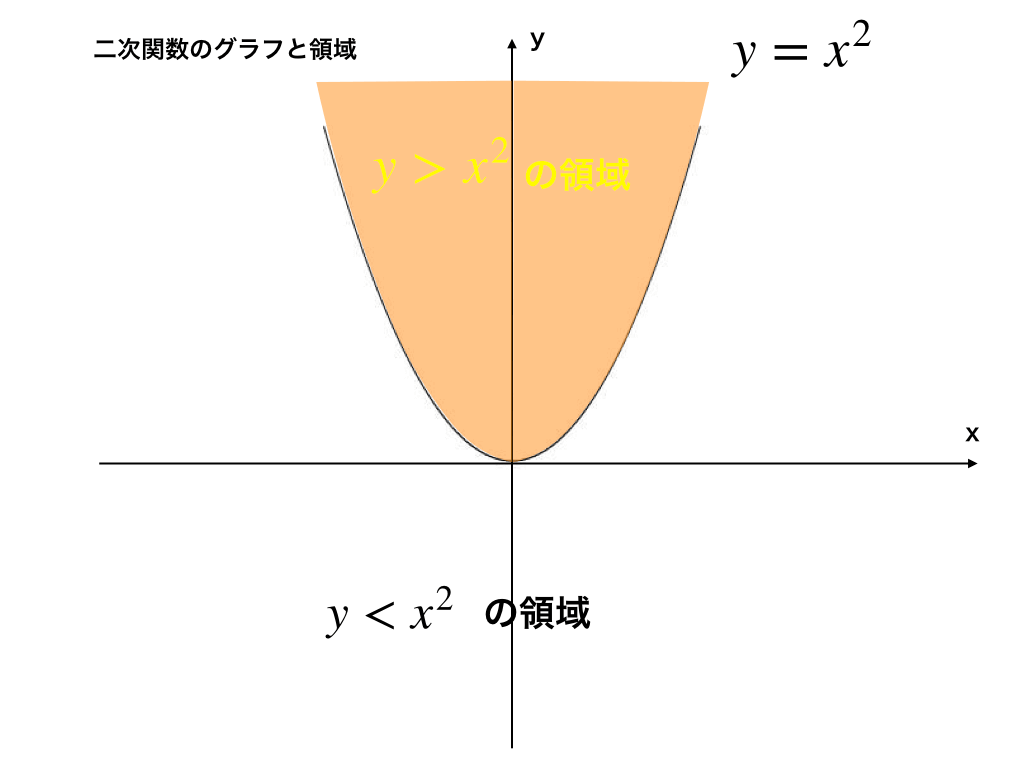
二次不等式の領域では、\(y=ax^{2}\)のaが正の時、\(y>ax^{2}\)が下の図のオレンジ色の部分を表し、\(y<ax^{2}\)がその外側の領域となります。
円の方程式と領域
円の方程式で表される部分を見ていきましょう。
中心\((\alpha,\beta)\)、半径rの円1の不等式:\(r^{2}>(x-\alpha)^{2}+(y-\beta)^{2} \)のとき、円の内側がその領域です。
また、\(r^{2}<(x-\alpha)^{2}+(y-\beta)^{2} \)ならば外側が不等式の示す領域となります。
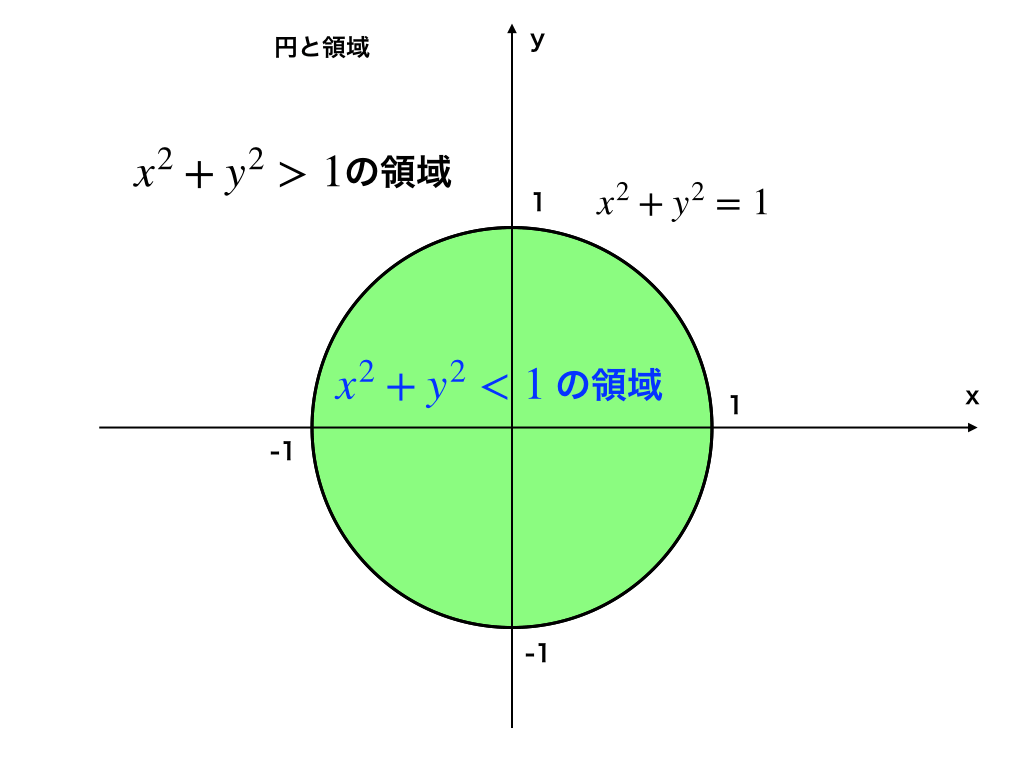
半径1、原点中心の円とその領域。
領域チェックのコツ(分からなくなった時+回答のチェック)・SPI対策にも~
たまに、不等式が表す領域がグラフの”内側なのか、外側なのか”や、グラフの”上側or下側”のどちらを示しているのか分からなくなる時があります。
また、複雑な領域を図示する問題では、解答を作った後に実際に合っているのかチェックしておきたい場合もでてきます。
そんなときには、『適当な座標』をその不等式に入れて『実験』してみると、即座に正しい領域をチェックできます。
例:y>x の不等式が示す領域がy=xの上か下かチェックする場合:
点(1,3)を不等式に代入すると、3>1 と矛盾なく成立します。
こんどは、点(1,0)を代入すると0>1となって成り立ちません。
これらのことから、グラフの上側がy>xの領域であることが分かります。
連立方程式・不等式と領域
ここからは、単一の不等式が示す領域から、複数(ここでは2つの)連立不等式が示す座標上の領域について見ていきます。
具体例で学ぶ:問題の解法と解説
問1:\(x^{2}+y^{2}<1\)と\(y>x\)の連立不等式が表す領域を図示せよ。
まずは、先ほど円と領域で使った\(x^{2}+y^{2}<1\)と、一次不等式のところで扱った、\(y>x\)の連立不等式が表す領域を考えます、
それぞれの領域を図示する
原点が中心で半径が1の円:\(x^{2}+y^{2}<1\)は内側部分で、・・・(1)
直線:\(y>x\)は上側部分の領域です。・・・(2)
2つの領域が重複している部分が答え
あとは、(1:青色部分)および(2)をともに満たす(=重複している)部分を調べると、次の図の「オレンジ色」で塗りつぶしたところが問題の領域であることが分かります。
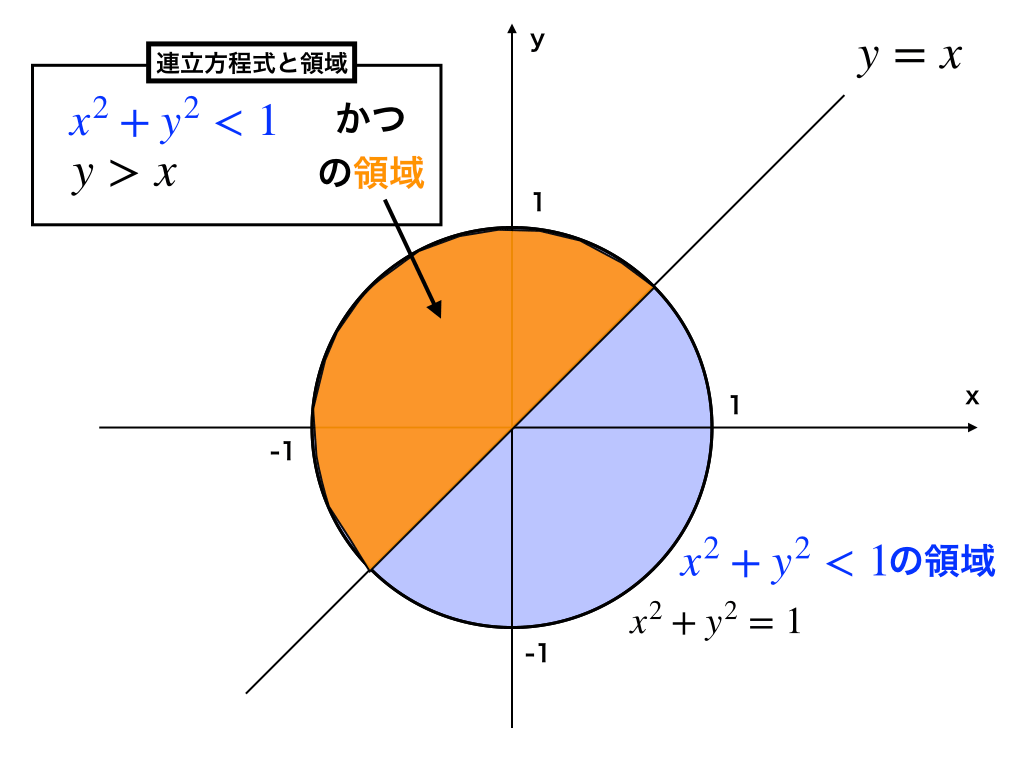
ただし、注意しなければいけない点として不等号の大なり・小なりの記号に=がついていないことから『境界』の”線”、および、”交点”は含まれない事があります。
この”等号の有無”による、【境界と交点について】書き忘れて減点されてしまう人が非常に多いので、注意して記載しておきましょう。
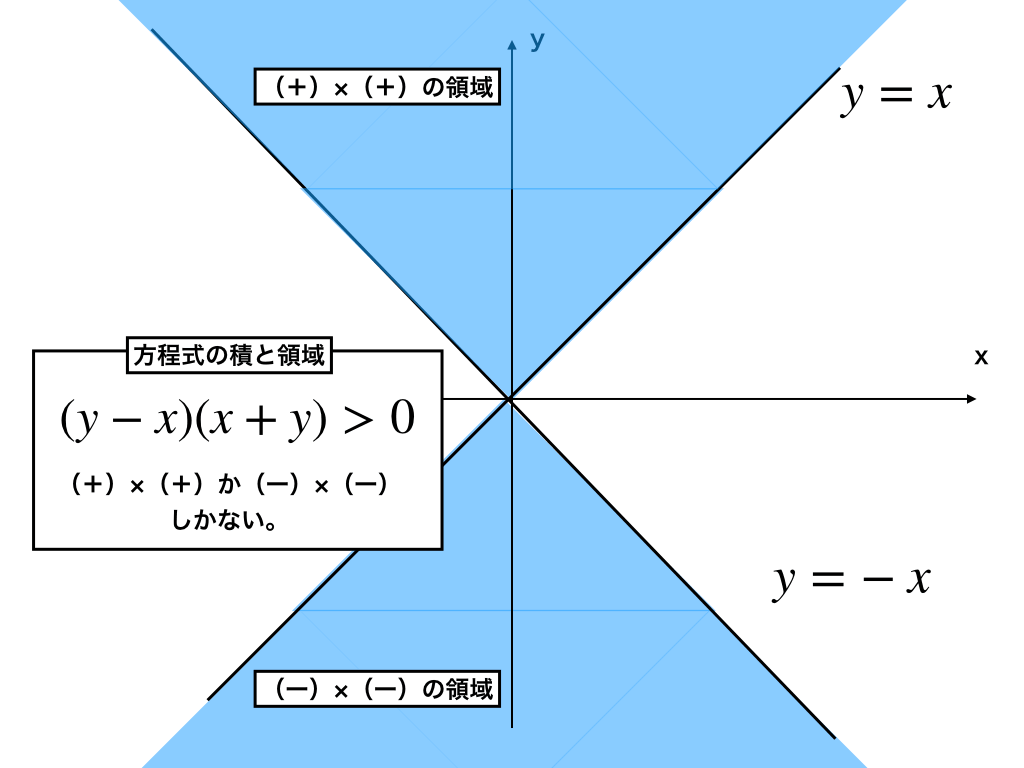
方程式の積と領域
『領域シリーズ第一回』の最後は、”(式)×(式)”という”方程式の『積』で表される部分”の領域の調べ方・図示の仕方を例題を通して解説します。
問題
次の不等式:$$(y-x)(y+x)>0$$を満たす領域をxy座標平面上に図示せよ。
解答と考え方:積の条件が正になる場合とは
一見難しく感じるかもしれませんが、単純にこの不等式を見ると、(y-x)と(y+x)をかけて正になる条件を考えれば解答できます。(非常にややこしい積の形になっても、基本的な考え方は同じです。)
掛けて正ということは、両方とも『正』であるか、両方とも『負』であるかのいずれかしか選択肢はないので、
(一):(y-x)と(y+x)がともに正:(y-x)>0 、かつ、(y+x)>0 の領域と、
(二):(y-x)<0 、かつ、(y+x)<0の領域を、
先ほどの連立不等式の領域の問題と同じように図示することで解答を得られます。
(+・+)と(ー・ー)それぞれの領域を図示する
実際の図は以下の通りです。
領域その一まとめと次回へ
・今回は今後の領域の問題を解いていく際に最低限理解して解くことができる必要がある『キソ』を解説しました。
・次回以降は、さらに複雑な領域の問題や、領域を応用して式の最大・最小を求める『線形計画法』などを紹介していきます。
図形と方程式シリーズ +領域の続編
〜〜軌跡と領域〜〜
第一回「(今ここです)領域の基礎」
↓(NEW!:2019/07/29作成しました)↓
第二回:「領域を利用した最大値・最小値問題の解法」
〜〜図形と方程式シリーズ〜〜
今回も最後までご覧いただきまして、ありがとうございました。
「スマナビング!」では、読者の皆さんのご意見・ご感想・記事リクエストの募集をコメント欄で行なっています。
・また、お役に立ちましたらぜひ snsでB!やシェアをしていただけると幸いです。
・その他のお問い合わせ/ご依頼、他に付きましては、お問い合わせページからご連絡下さい。

