
平均値の定理(基礎編)
何となくよくわからないままにスルーしがちな「数学Ⅲ:【微分法の応用】での平均値の定理」。
実は「もっとも役に立つ定理」という異名があるほど、身につけると入試はもちろんそれ以降でも大活躍する理系必須の定理なんです!
今回はその基礎編として、“初めて習う人でも”最短で理解出来るように解説し、過去問を解いて知識を固めていきます。
目次(タップした所へ飛びます)
平均値の定理とは?
まずは、教科書的な定義を書きます。
なお、「微分可能や連続についての違いと意味」で「微分可能」や「連続」という言葉について解説しているので、曖昧な人は参照してみてください。
関数f(x)についてa≦x≦bの範囲で微分可能ならば、
$$\frac {f\left( b\right) -f\left( a\right) }{b-a}=f'\left( c\right)・・・(※)$$
となる実数cが、aとbの間に少なくとも一つは存在する。
文字だけ見ると分かりにくいので、図で見てみましょう。
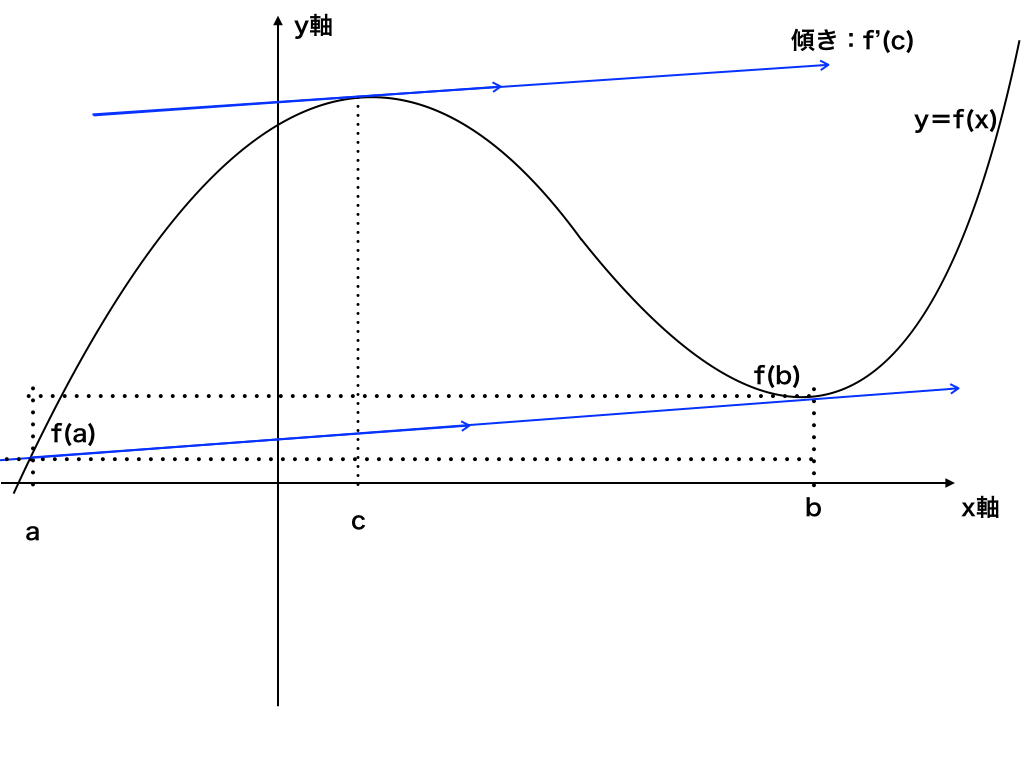
<図1>
上図の様にxy平面上の関数f(x)のグラフで点A(a,f(a))と点B,(b,f(b))を取ります。
この点Aから点Bの間で、「微分可能=連続でなめらか」の時の点A、点B間の傾きを計算します。
$$\frac{yの変化量}{xの変化量} より⇔\frac{f(b)-f(a)}{b-a}\cdots (*)$$
(*)が(※)の左辺にあたり、
(※)の右辺はf(x)を微分してa以上b以下のcを代入したもの
⇔aからbまでの間のどこかの点C(c,f(c))における”傾き”にあたります。
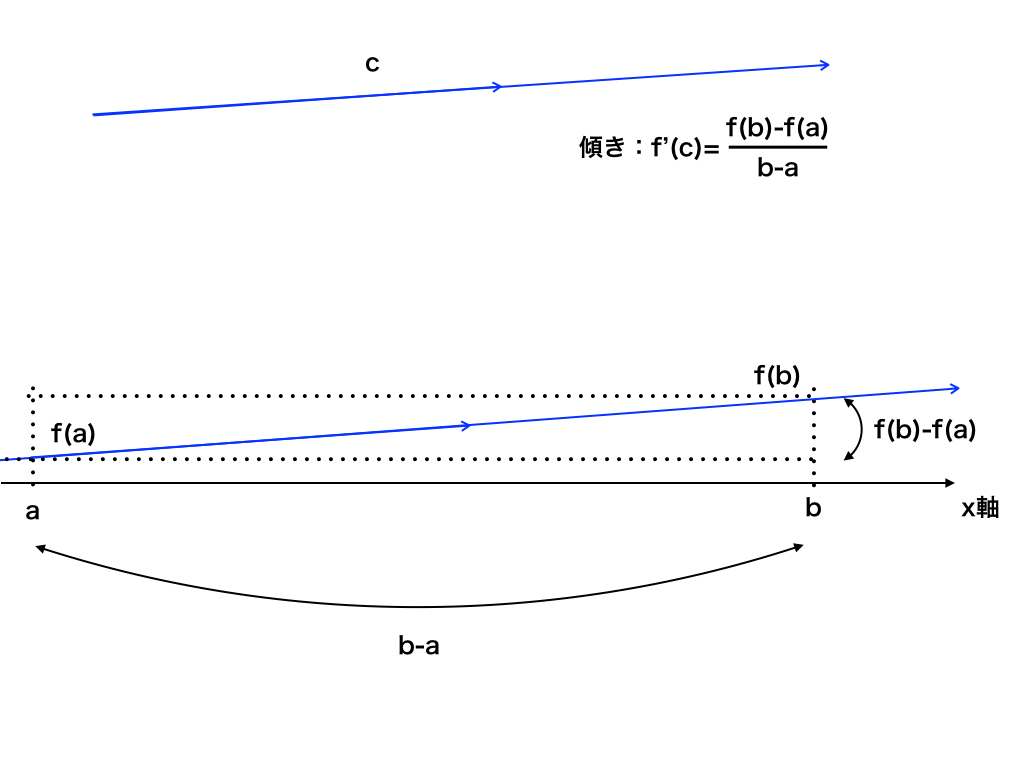
つまり、平均値の定理とは、「AB間が微分可能な時、【点AB間の傾きと同じ傾きを持つ接線がひける点C】が点AB間に必ず一つ以上存在する」という意味です。
平均値の定理の使い方<使用サインを見逃すな>
平均値の定理を利用する最も基本的な問題は《不等式の証明》です。
その際<平均値の定理を使うこと>を知らせてくれる絶対に見逃してはいけないサインがあります。
不等式の証明での利用
実際に、問題を通してみていきます。
例題1:
全ての正の数a、bについて、
\(a(\log{a}-\log{b})≧a-b\)であることを示せ。
この問題の様に、\(f(◯)-f(△)>◯-△\)や、
\(\frac{f(◯)ーf(△)}{◯ー△}の形\)があれば、そのほとんどが【平均値の定理を使うサイン】です!
以下順を追って解説していきます。
解説
・とにかく左辺のカッコの内側に\(\log{a}-\log{b}\)、\(右辺にa-b\)があるので、平均値の定理のサインであると気付きます、
\(a(\log{a}-\log{b}) \)
実際の問題文は上の様にaがかかっていますが、
大体の場合自然と処理する事ができるので、大きなサインを優先します!
ここで、平均値の定理のf(◯)に当たるものがどれかを考えると、\(\log{a}\)が良さそうです。
・まず平均値の定理が使える前提である「aからb」で微分可能であることを記述します。
\(f(x)=\log{x}はx>0\)において微分可能である。a,bともに正の数よりf(x)はa,b間で微分可能。
\(f(x)=\log{x}\)として、微分すると
$$f‘(x)=\frac{1}{x}$$
・与式を平均値の定理のカタチで使う際の場合分けを考える
(※:分母が(a-b)になるので、aとbの大小関係によって不等号の向きが変わります。またa=bの時は(a-b)=0になるので割れません。)
(ⅰ)a>bの時
平均値の定理より、
$$\frac{f(a)-f(b)}{a-b}=f’(c)=\frac{1}{c}を$$
満たす実数cが0<b<c<aに存在する。
(※:ここで、0<b<c<aの大小関係を利用して逆数を取ります)
$$\frac{1}{a}<\frac{1}{c}<\frac{1}{b} より、$$
$$\frac{1}{a}<\frac{1}{c}=\frac{\log{a}-\log{b}}{a-b}$$
$$⇔\frac{1}{a}<\frac{\log{a}-\log{b}}{a-b}$$
したがって、\(a-b>0よりaーb<a(\log{a}- \log{b})が成立する。\)
(ⅱ)a=bの時
a=bのとき、\(0=aーb=a(\log{a}- \log{b})\)が成立する。
\((※ a-b=0⇔\log{a}=\log{b}より)\)
(ⅲ)a<bの時(不等号の向きに注意)
(ⅰ)の時と同様に、平均値の定理より、
$$\frac{f(a)-f(b)}{a-b}=f’(c)=\frac{1}{c}を$$
満たす実数cが0<a<c<bに存在する。←(※順序が(ⅰ)と逆になっていることに注意)
逆数を取り、
$$\frac{1}{b}<\frac{1}{c}<\frac{1}{a} より、$$
$$\frac{1}{a}>\frac{1}{c}=\frac{\log{a}-\log{b}}{a-b}$$
$$⇔\frac{1}{a}>\frac{\log{a}-\log{b}}{a-b}$$
が成り立つ。ここで(aーb)<0より、
(※符号の向きに注意して、)
\((aーb)<a(\log{a}-\log{b})が成り立つ。\)
以上の(ⅰ)〜(ⅲ)をまとめる。
(ⅰ)〜(ⅲ)より、正の数a,bに対して常に与式:\(aーb≦a(\log{a}ー \log{b})が成立\)する。
また、等号が成り立つ条件は(ⅱ)a=bの時のみである。
・・・(証明終了)
平均値の定理の応用編へ(+α)
次回は、平均値の定理の更なる応用問題を解きながら解説を進めていきます。
不等号や証明で読んでおくと役立つ記事
ここでは、問題文と解説中に出てきた「不等式の証明」や「逆数」の扱い方を解説している記事を紹介しておきます。
(整数分野ですが、応用できる考え方が詰まった記事です。)
「逆数を取って絞り込む!条件式に不等式が入った問題の攻略法」
<関連記事>
<当サイトからのお願い>
・多くの学生・受験生に利用して頂くためにSNSでシェア(拡散)&当サイト公式Twitterのフォローをして頂くと助かります!

