ランダムウォークと確率(高校数学+α)
今回は、ランダムウォークと呼ばれるものの簡単な由来・意味を紹介し、難関大でも出題されやすい確率の問題(本題はこちらです)を解説していきます。
目次(タップした所へ飛びます)
ランダムウォークとは
名前の通り、確率的に不規則・無作為(ランダム)に点が移動する現象(かなり大雑把ですが、厳密に解説すると大学以降のレベルになるので、今はこのくらいの理解で良いと思います。いずれ統計の分野で追記します)
その過程を見ると、酔ってランダム(不規則)に歩く人の足跡の様になっていることから『酔歩』とも呼ばれます。
この様なランダムウォークは様々な分野で見ることができます。高校化学でも習うブラウン運動を例に挙げておきます。
ブラウン運動
化学を勉強している人なら、コロイドのところで『ブラウン運動』というものを習うはずです。
特殊な顕微鏡で花粉(が浸透圧によって破れ、そこから出てきたさらに小さい粒子)などの”コロイド粒子”を観察すると、ブラウン運動と呼ばれるコロイド粒子が不規則に運動している*様子を観察することができます。
(*実のところは、顕微鏡で見えない水分子(や溶媒分子など)が熱運動によってコロイドにぶつかり、結果として”コロイドが動いているかの様に”見えているのですが。。)
株価や座標上の位置
この様な不規則な動きをするものはコロイドだけでなく、有名なものとして株価(議論はありますが)などがあります。
確率の問題への利用
今回は、このランダムウォークの考え方を題材とした確率の有名問題を扱います。
コインと持ち点の変化の問題
コインを投げて、表(以降Hとする)が出たら1点獲得、裏(以降T〃)が出たら一点を失うゲームがあるとする。(※:H:Head=表、T:Teal=裏)
問題1:はじめの持ち点が0点で、6回コインを投げた。この試行が完了したとき持ち点が0点となる確率はいくらか。
問題2:今度は持ち点0点の条件は同じで、5回コインを投げた。結果が0点である確率を求めよ。
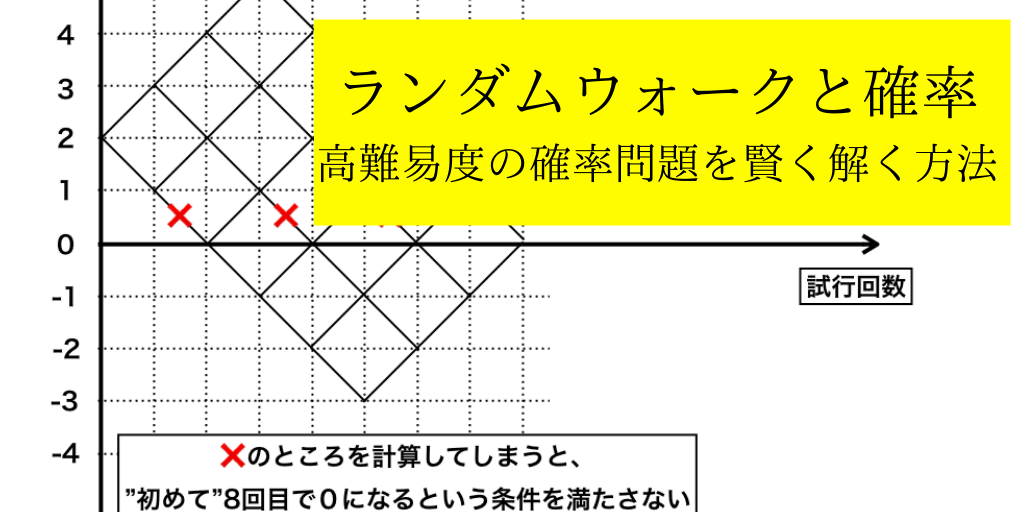
問題3:はじめの持ち点を2点とし、8回コインを投げた。8回目の試行が終了した時点で『初めて』持ち点が0点となる確率を計算せよ。
解法と解答解説
この問題1〜3は、コインを繰り返し投げるという試行を繰り返しているので基本的に次の>>反復試行の確率について<<の考え方を用います。
ただし、それによって持ち点が上下したり『2度目に0点となる』や『初めて0点となる』の様な複雑な条件がくっ付いています。
そのため、初めはなかなか手を出しにくい難易度の問題です。
条件をグラフ上で見える化してみる
このサイトでは何度も繰り返し言っているのですが、特に整数や確率などの分野の難問では、『まずは実験をしてみる』ことが大切です。
例えば、H、H、H、T、T、Tならば+1+1+1ー1ー1ー1=0となって条件を満たします。
ここでもう少し実験を楽にするために得点の変化を数字ではなく矢印を使ってみます。
H、H、H、T、T、Tなら、↑↑↑↓↓↓=0とかけます。(具体的に点数で書くと、1点2点3点2点1点0点の推移をたどります)
ここまでで、感の良い方なら『↑』と『↓』が3つずつ並ぶ順列を応用すれば良いことに気がつくかも知れません。(実際次の項で説明します。)
が、問題三ではそれで上手くいかなくなるので、以下の様に(ポイントー試行回数)を軸とする平面を用いる解法を知っておいてください。
<得点-試行回数がx、y軸に対応する座標平面で考える>
最短経路問題へ帰着させる
この方法の肝は、下の図の様にナナメ向きの格子を作るところにあります。
例えば1回目の試行でHが出れば(1,1)に移動、Tが出れば(1,-1)に移動という風に視覚的に問題をとらえることができます。
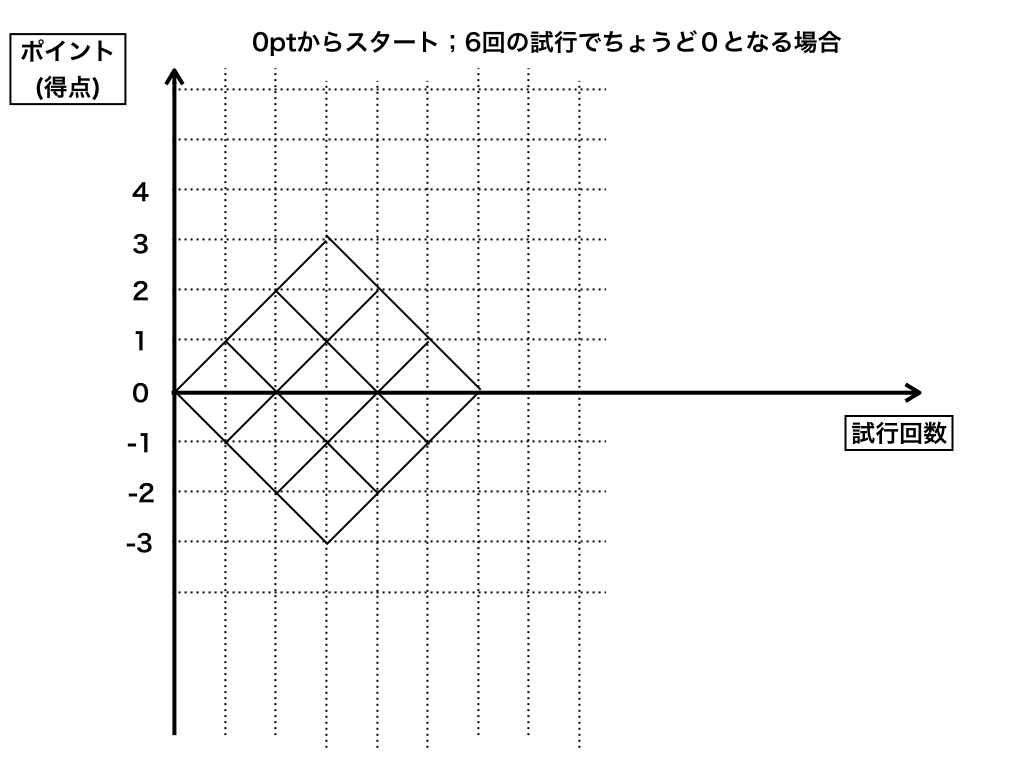
<問題1>
さらに、この”格子状”で表すことにより↓の記事で解説している
『最短経路』の問題に帰着させることができるのです。
問1では、特に条件が付いていないので”斜め向きの格子に書き込む方法”でも、次の図の様に『同じものを並べる順列』の考え方を用いても良いです。
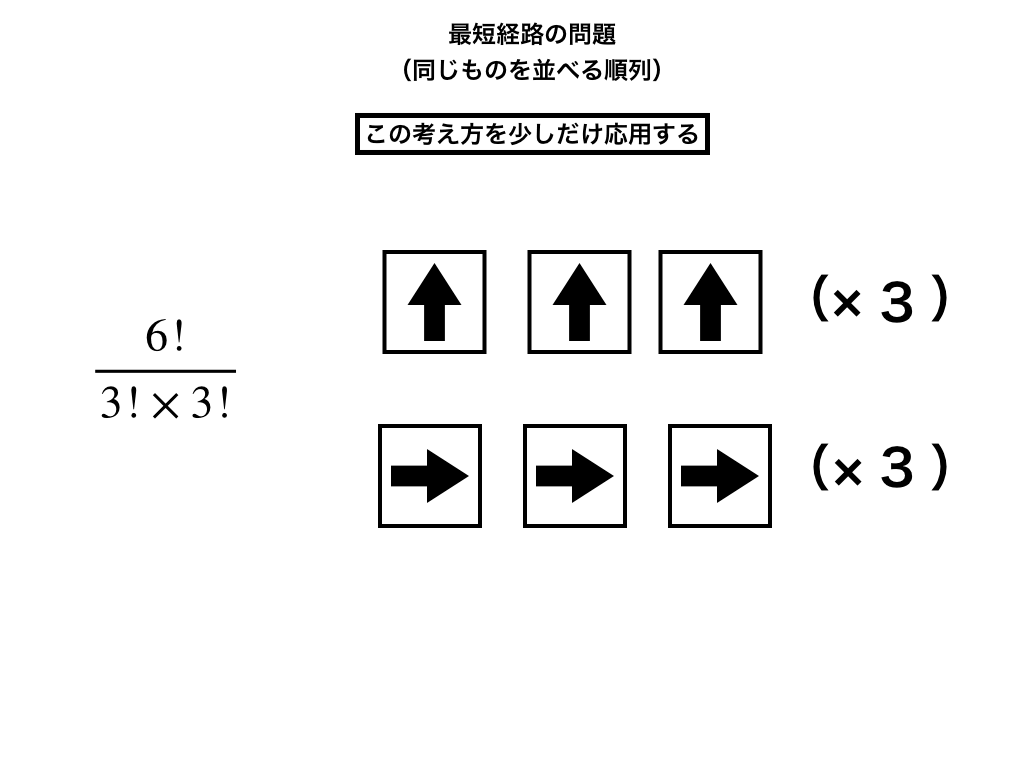
重複順列の方法で考えると、$$\frac{6!}{3!3!}=20(通り)$$
もちろん書き込む方法でも20(通り)。
全事象は\(2^{6}=64(通り)\)なので
したがって、確率は$$\frac{5}{16}・・・(答)$$
反復試行の確率 の考え方で、
$$(\frac{1}{2})^{3}\times(\frac{1}{2})^{3}\times {}_6C_{3}=\frac{5}{16}$$
でも当然OKです。
奇数回の場合
では問題2に移りましょう。これも同様にできる・・・と良いのですが、少し実験してみましょう。
0点から0点に5回=奇数回でたどり着くことは可能でしょうか?偶数回オモテが出ると奇数回ウラ、その逆も成立します。(偶数+奇数=奇数、偶数+偶数=偶数、奇数+奇数=偶数)より、どう頑張っても奇数回で元の0点に戻ることは不可能です。
したがって、問2の確率は0・・・(答)
制限のある問題と工夫
さて、問三はstartが”2点”からで、試行回数は”8回”なので、問一と同様のナナメ向きの格子を描くと以下の様になります。
6点以上を獲得してしまう(=すなわちHが4回でる)と、残りの4回全て裏:Tが出ても0点には戻れません。
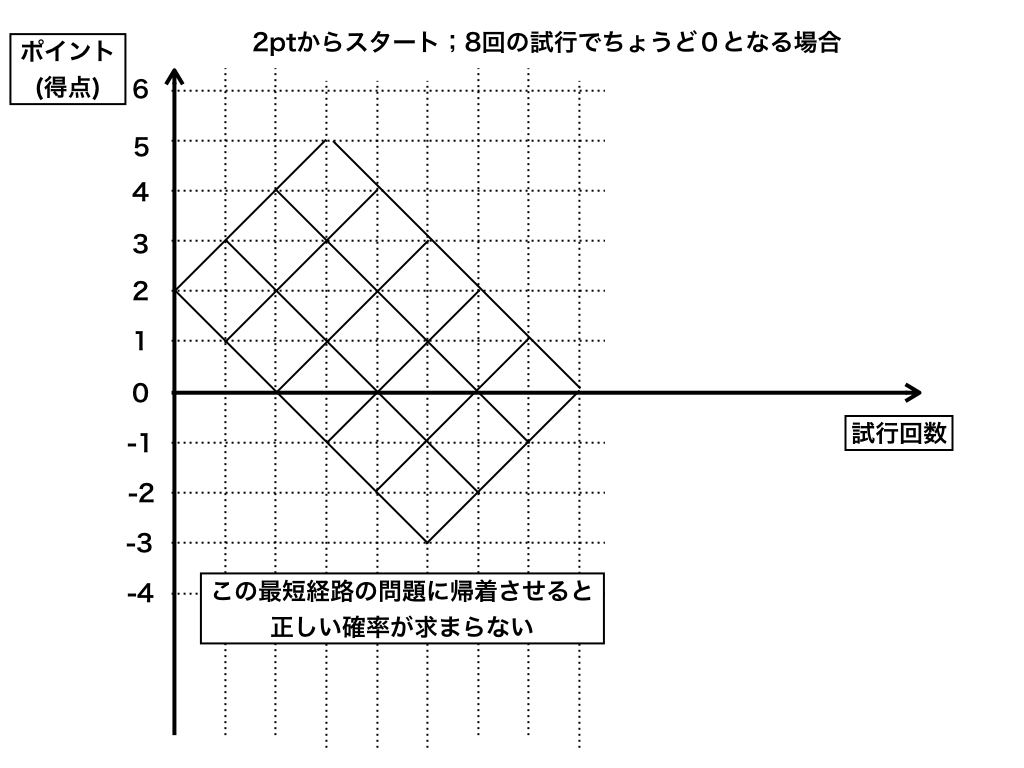
さらに、重要な点として『初めて”8回目で”0点になる』という厳しい条件が付いているので、上図を問1の解法で解くとバツになってしまいます。
→【(2,0)や(4,0)の様な点も数えると”初めて8回目で〜”を満たさないため】
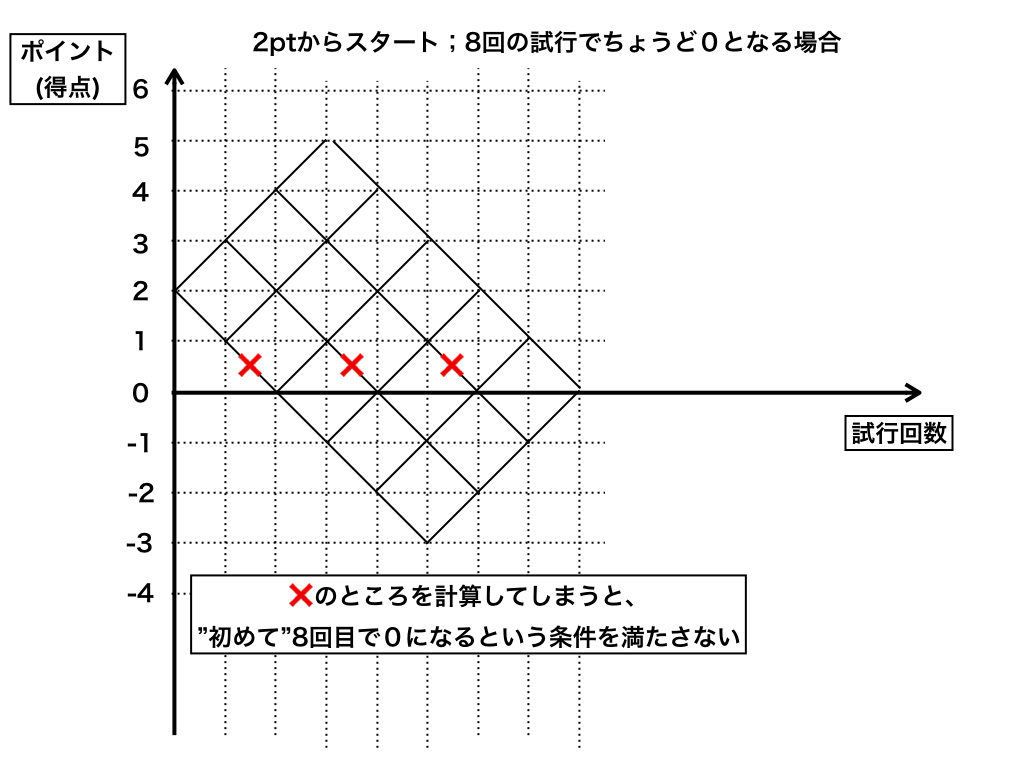
<問題3ー格子の工夫>
そこで、今回の最大のポイント(コツ):『条件を満たさない経路を”×”でふさぐ』方法をとります。
そうして、格子の部分だけを取り出したものが↓です。
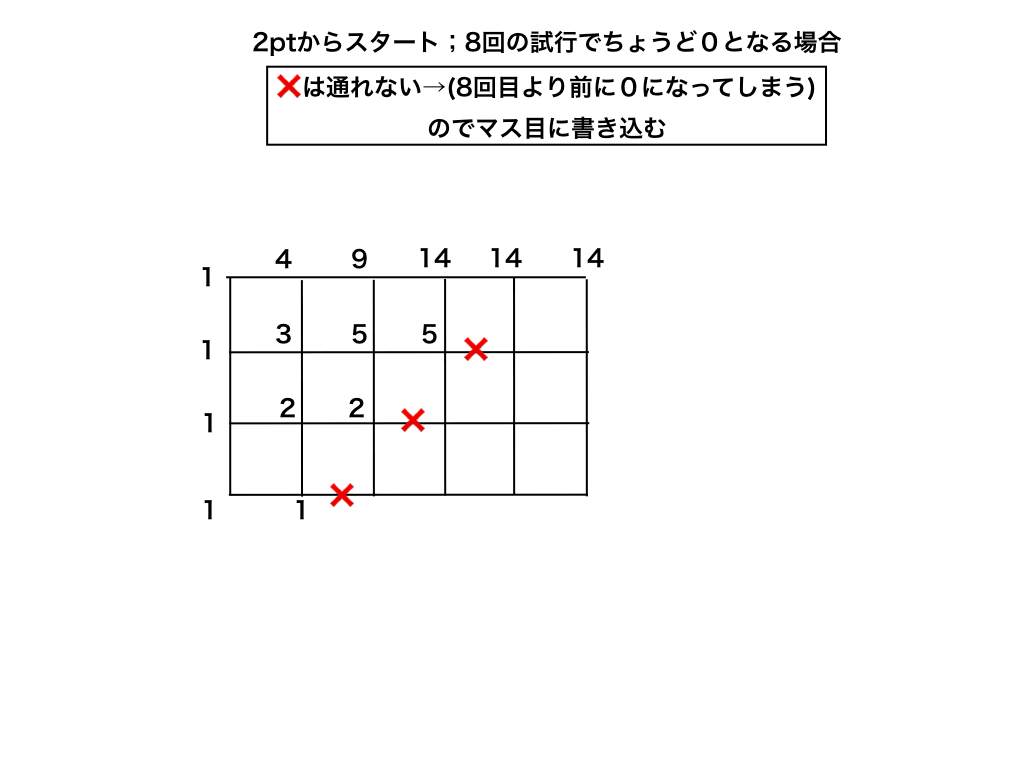
試行回数の軸(x軸)に引っかかっている部分を赤いバツで消します。
(もしこのバツの付け方がわからなくなったら、『実験』してみましょう。スタート地点である左下から↑(3点,1回)→(2点,2回)→(1点,1回)と進み、もう一度右→へ進むと(0点,4回)となって条件を満たさないので赤の部分は通れません。他の二箇所のバツも同じ方法で確かめることができます。)
こうすれば、あとは図に書き込む方法(最短経路の記事参照)を使用して、14通りであることが分かります。
問われているのは”確率”なので、全事象が\(2^{8}=256通り\)
ゆえに、$$\frac{14}{256}=\frac{7}{128}・・・(答)$$
酔歩(ランダムウォーク)と確率まとめ
大学受験のレベルでは、問題3のレベル+α程度までしか出ませんが根底にある”ランダムウォーク”の概念は非常に幅広い分野(経済学・数学・統計学・物理学etc,,,)で利用・応用されています。
興味を持った人は、ぜひ大学で詳しく学んでみてください。

