
斜方投射・放物運動と軌道の式
前回の記事:「等加速度運動と鉛直投げ上げ」に引き続いて、
その応用である斜方投射、放物運動の解説と、『軌道の式』の作り方を紹介していきます。
(続編:「モンキーハンティングと相対速度」を作成しました。)
目次(タップした所へ飛びます)
斜方投射と放物運動の軌道の式
・斜方投射を見たら分解せよ
・斜方投射の例題1
・例題1の解説
・速度を分解する
・放物運動の特徴を利用する
・斜方投射された球の軌道の式
・軌道の式をどう使うか?
・まとめ
斜方投射を見たら分解せよ
そもそも斜方投射とは以下の<図1>の様に、地面から仰角θ、一定の初速度V0で投げ上げる運動をさします。
斜方投射で問われるものは大体決まっており、以下の4点に主に集約されます。
・最高点の高さhmax、
・その時の時間tmax、
・地上に戻ってくる時の時間
・その座標(投射位置からの水平距離)
発射される向きはナナメですが、ベクトルの分解の要領<参照:「物理基礎でつまずかない為のベクトルと三角比」>で、
・「先に軸を定めてから」三角比をつかって「鉛直投げ上げ運動」と「等速直線運動」に分解させれば、決して難しい問題ではありません。
斜方投射の例題
(例題1)今、<図1>の原点の位置から仰角θ、初速度V0(m/s)で球を投射する。
重力加速度をg( m/s2) として、
球の最高点hmax(m) とその時刻tmax(s) 、
及び球が再び地上に落下した場所の位置X(m)と時刻T(s)を求めよ。
但し空気抵抗は無視できるものとする。
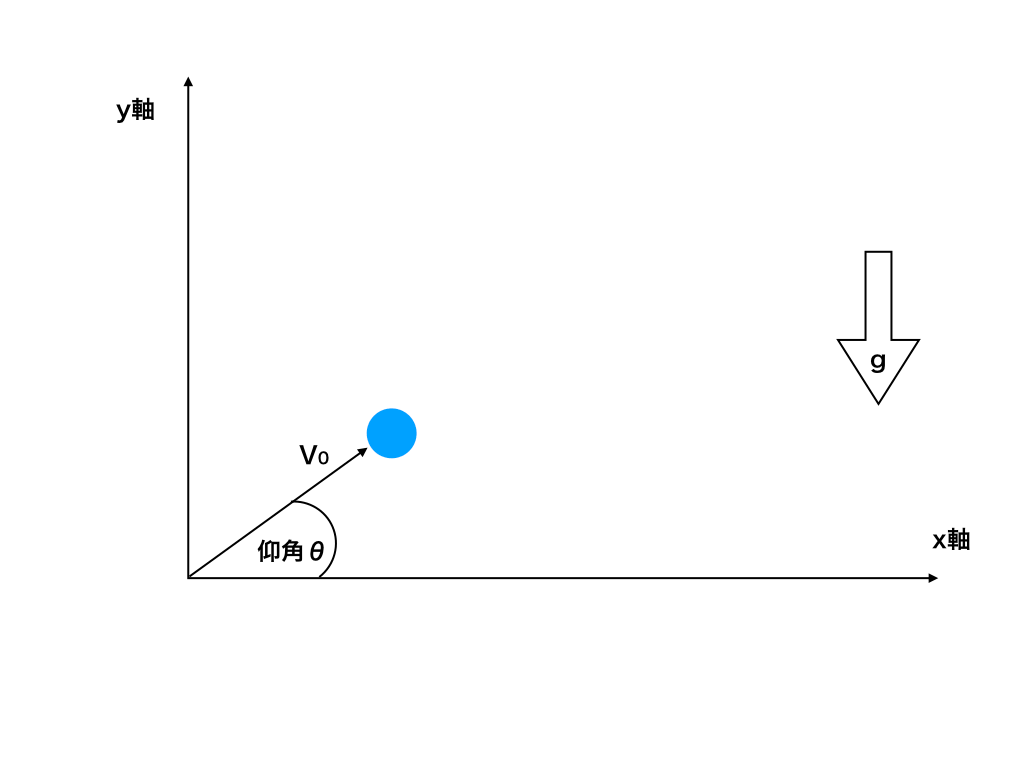
<図1:斜方投射(例題1)の図>
例題1の解答解説
<方針>軸の設定と初速度の分解
力学は「軸の設定が全て」と言っても過言でないほど大切です。
今回の問題では<図1>の“鉛直上向きを正としたy軸”と“水平方向右向きを正としたx軸”に設定することにします。
軸の設定を終えたら、初速度を鉛直方向(y軸方向)と水平方向(x軸方向)に分解していきます。
そしてこの運動においては、
y軸マイナス方向に重力加速度gがかかっているので、この斜方投射の運動は、
・「鉛直方向」には加速度ーg(m/s2)の等加速度運動
・「水平方向」には何の加速度もかかっていないので、等速運動に分解して考えていきます。
速度を分解する
<方針>取りあえずVxとVyを計算すると、等加速度運動の3式より、
\(v_{x}=V_{0}\cosθ \)
\(v_{y}=V_{0}\sinθ -gt\)
最高点とその時刻の公式
「最高点を一瞬で出すtechnic」より、最高点h maxとその時刻tmaxの求め方を紹介しましたが、こちらもそのまま利用可能です。
最高点は、
\(h_{\max }(m) =\frac {( v_{0}\sinθ) ^{2}}{2g}\)
最高点での時間は、
\(t\max (s) =\frac {v_{0}\sinθ }{g}\)
(ただし式の初速の部分が分解されているので、そこだけが変わっています)
例題1の球はつぎの項で示しますが、放物線を描いて運動します。
放物運動の特徴を利用する
そして最高点の水平位置を軸として、対称に落下していくので、
まず球が最高点にいるときのx座標(xmax)を求めます。
その2倍の距離の地点Xに落下するので、落下時刻Tも同様にtmaxの2倍で求めることができます。
\(T=\frac {2v_{0}\sinθ}{g}\)よってTが求まりました。
次に落下地点のx座標\(X=v_{0}\cosθ× 2t_{\max }\)、
\(X=v_{0}\cosθ×2× \frac {v_{0}\sinθ }{g}\)
$$X=\frac {2v^{2}_{0}\sinθ \cosθ }{g}$$以上でXも求まりました。
斜方投射された球の軌道の式
次に、斜方投射の軌道の式について学びます。
今、球のx座標とy座標は次のように求められます。
\(x=v_{0}\cos \theta t\)
$$y=v_{0}\sin \theta t-\frac {g}{2}t^{2}$$
媒介変数のtを消していくと次のような式が出来上がります。
$$x=v_{0}\cosθ t⇔ t=\frac {x}{v_{0}\cos \theta }$$
tを代入して、
$$y=v_{0}\sin \theta ( \frac {x}{v_{0}\cos \theta }) -\frac {g}{2}( \frac {x}{v_{0}\cos \theta }) ^{2}$$
$$y=\frac {v_{0}\sin θ}{v_{0}\cosθ}( x) -\frac {g}{2}( \frac {x}{v_{0}\cosθ })^{2}$$
$$y=\tan \theta (x) -\frac {g}{2v^{2}_{0}\cos ^{2}θ }(x)^{2}$$
$$y=-( \frac {g}{2v^{2}_{0}\cos ^{2}θ}) x^{2}+\tan θx$$
これは、まさに\(y=-ax^{2}+bx\)のタイプの二次関数を表しています。
従って、球の軌道は上に凸な放物線を描くことが式からも確認できました。
軌道の式をどう使うか
さて、この一見ややこしい式はどの様に役に立つのでしょうか。
一つの例としてy=0、xで右辺をくくるとy座標が0の時,
すなわち投射時のx座標と落下地点のx座標を求めることが出来ます。
その他にも、頂点の座標や任意のx座標でのy座標を求めることなど、色々な問題に応用できます。
まとめと続編へ
次回は斜方投射の総仕上げとなる「モンキーハンティングの解説」(作成済み)を行います。
これまでの知識が活躍するので、よく復習しておいて下さい!(「鉛直投げ上げ運動(シリーズその1)」)
>>「力学が苦手な人〜難関大レベルまでの解説記事総まとめ!」<<
今回も最後までご覧頂きありがとうございます。
現在、解説して欲しい単元やご感想を募集中です!(数学/物理/化学/地理/公民)是非コメント欄にお願いします!お疲れ様でした。

