
位置ベクトルとは?ベクトル入門第3回
<この記事の内容>:『位置ベクトルがわからない・・・』、『普通のベクトルとどう違うの?』、『位置ベクトルと“点”の関係で混乱している』といった方のために、0から位置ベクトルを解説していきます。
また、全く初めてベクトルに触れる方は「第一回ベクトル入門(1)」←このリンクを先に読んでおいてください。
目次(タップした所へ飛びます)
位置ベクトルって何?
これはベクトル方程式って何?と共にベクトルで苦手意識を持つ人が多い分野です。
(ベクトル方程式は→「ベクトル方程式とは?イラストで解説」をご覧下さい!)
どちらもイメージがしにくい為に、あいまいなままにしてしまう人が多いです。
が、今回扱う位置ベクトルは一度理解すると非常にシンプルです。
位置ベクトルの正体
ベクトルは、”長さ”が決まっていて、”向きを持つ”ものでした。
すなわち、『ベクトル=有向線分』なんだ!という解説を第一回でしました。
(危うい人は第一回「ベクトルとは?はじめから教えます!入門第1回」へ・・・)
ということは、始点(基準点)を決めてしまうと、そのベクトルの終点(矢印の先)も自動的に決定されます。
座標平面上の点とベクトル
これまで、座標平面(xy平面)で点の位置を表そうとする時には、原点(0,0)を基準にして、点P(3,5)の様に表示をしていました。("図形と方程式"の範囲)
これをベクトルで表したのが位置ベクトルの考え方といえます。
まず、基準とする点Oを決めます。
(点Oの場所はどこにとっても良いですが、原点に点Oを置く事が多いです。)
そして、平面上の点Aに対して\(\overrightarrow{OA}を\vec{a}とします。\)
位置ベクトルは点では無い
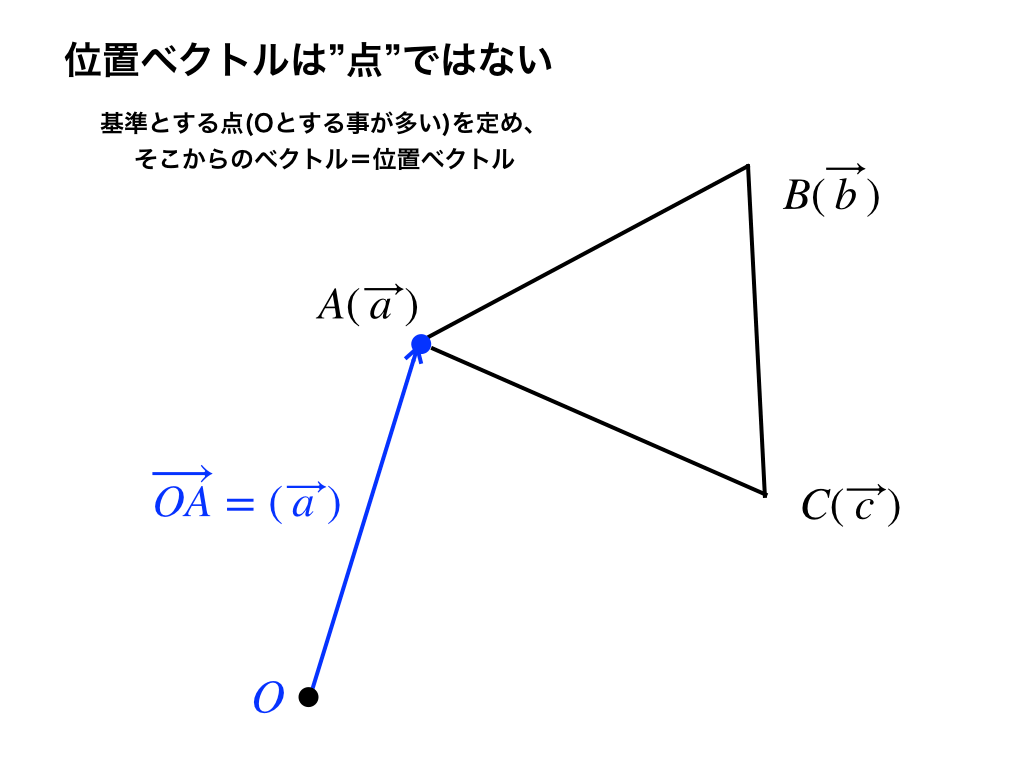
このとき、上に書いた様に始点は点O、ベクトルは向きと長さが決まっているので、
点Aへのベクトル\(\vec{a}\)は一通りしかないですし、その逆を言えば、\(\vec{a}\)の先にある点はAしかありません。
この様に、ベクトル\(\vec{a}\)と点Aは1対1に対応します。
そこで、\(\vec{a}\)の事を『点Aの位置ベクトル』といい、A(\(\vec{a}\))で表すことにしました。
ただし、あくまでも基準点からある点(ここでは点A)を“ベクトル”で示したものなので、”位置ベクトル=点”な訳ではありません。(ここで引っかかりやすいので要注意です。)
内分・外分点の位置ベクトル
さて、何となくでも『位置ベクトル』の意味がわかってきたでしょうか?
ここからは、内分点・外分点の位置ベクトルについて見ていきます。
図形と方程式や、複素数平面での内分点・外分点は、「内分・外分の公式と図示の仕方」で解説しています。あわせて参考にしてください。
内分点・外分点の公式
次の図のような、三角形ABCの辺BCを『m:n』に内分するとき、
$$\frac{n\vec{a}+m\vec{b}}{m+n}$$
同様に、『p:q』に「外分」するときの公式は、
$$\frac{-q\vec{a}+q\vec{b}}{p-q}$$
重心の位置ベクトル
次は《重心の位置ベクトル》についてです。
重心の位置ベクトルについては、
・基準点を三角形ABCの外側の点Oに置いた場合(一)と
・混乱しやすい、基準点を点A(や、B、Cなど三角形の頂点のいずれか)に置いた場合(二)
の2通りを解説します。
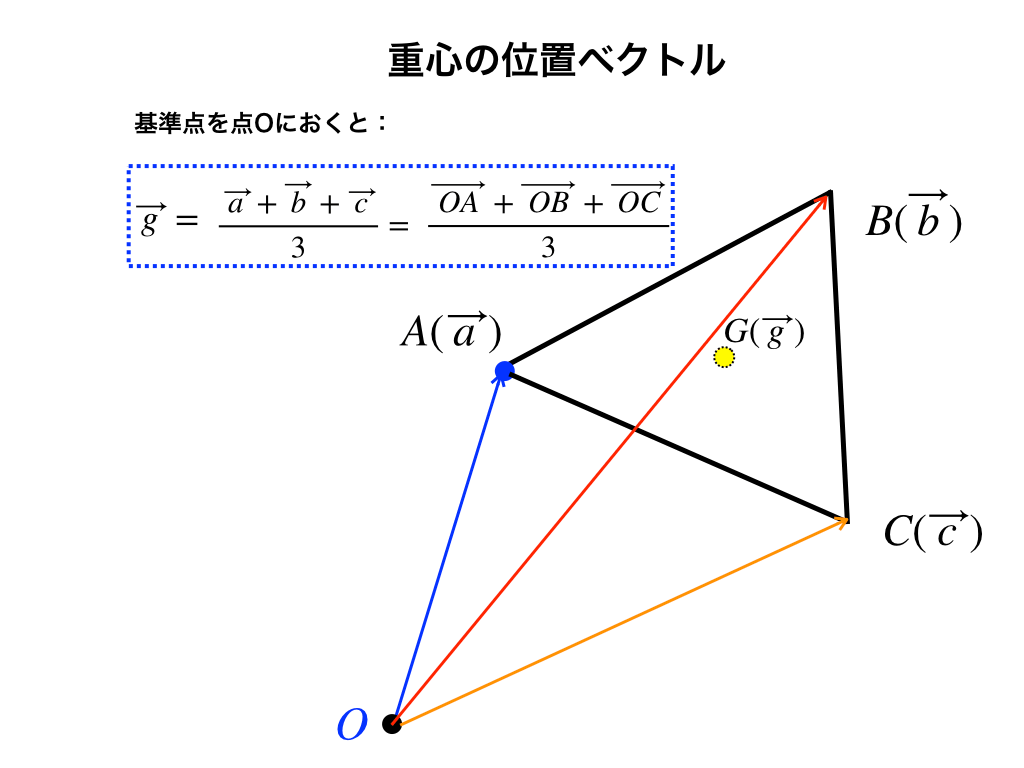
三角形の外側を基準にする(一)
図のように、点Oを外部に置いて三角形ABCの重心G\(\vec{g}\)を位置ベクトルで表すと
\(\vec{g}\)
\(=\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}\)
よって
$$\vec{g}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}$$
重心の位置〃(二)
上でも書いたように、三角形の頂点のいずれかを基準点にした場合は要注意です。
こちらも以下の図を見ながら解説すると、重心:点Gへの基準点Aからの位置『ベクトル』は、
\(\vec{g}\)
\(=\frac{\overrightarrow{AA}+\overrightarrow{AB}+\overrightarrow{AC}}{3}\)
よって、
$$\vec{g}=\frac{\vec{b}+\vec{c}}{3}$$
と表せます。
もし、(”点”として位置ベクトルを捉えてしまうと、\(=\frac{\vec{b}+\vec{c}}{3}\)このような式を見たときに??となってしまいます。)

位置ベクトルを使う理由(の一つ)
別に位置ベクトルなどを持ち出さなくても、図形と方程式でやった様に、座標を(x、y)で表して問題をといて行けば良い様に思えます。
しかし、図形と方程式ではxyの直交座標を使っているので、斜めの線や三角形、五角形などx軸/y軸に平行でない図形の問題を解こうとすると、一気に大変になります。
(例えば、三角形の斜めの辺に垂直な線を求めようとすると、まず斜めの辺の方程式を計算して、【その傾き・垂直な線の傾き=-1】、そして切片をを求めなければいけない事になります。)
ところがベクトルは特にxyの軸にしばられることなく、計算が楽になるような《斜めのベクトル》でも使うことができます。
ベクトルの分解
今回はもう一点、ベクトルの分解について紹介しておきます。
座標上に点O(基準点)、点A、点Bがある時、ベクトルを使って$$\overrightarrow{AB}=\vec{b}-\vec{a}$$ とかけます。
なぜなら、点Aから点Bへ向かう方法としては、直接点Aから点Bへ向かう道順・・・(三)と、
いったん点Aから点Oへ逆向きに進み・・・(四-1)、点Oから点Bへ向かう道順・・・(四-2)があり、
(四-1):AからOへは\(-\vec{a}\)(aベクトルの”逆ベクトル”)、
(四-2):OからBへは\(\vec{b}\)と進めるからです。
そしてーaベクトルは\(-\overrightarrow{OA}\)、bベクトルは\(\overrightarrow{OB}\)なので、\(\overrightarrow{AB}\)=\(\overrightarrow{OB}-\overrightarrow{OA}\)と書くことができます。

つまりOを基準に考えると、ベクトルABは『後(B)ー前(A)』に分解できるという事です。
この”ベクトルの分解”はベクトルの幅広い分野で非常に頻繁に使うので、確実に使えるようになっておいて下さい。
位置ベクトルまとめと関連記事へ
いかがでしたか?「位置ベクトル」については、まだ今の段階ではまだ「漠然とした」理解かも知れません。
が、いろいろな問題を解き、そのたびに使っていくと自然に慣れてくるので、どんどん演習用の問題を解いていって下さい。
ある程度理解できたと思ったら、
問題を解いてみる。
→20分くらい考えても分からなければ、解答を見て真似をする。
→しばらく時間をおいて、何も見ずにもう一度解いてみる。
という流れを繰り返すことで、もっとも効率よく苦手分野を克服することが可能です。
ベクトルまとめ記事へ
ベクトルの解説記事のまとめは→「ベクトルとは?ゼロから始めて最難関レベルまで!徹底解説9選」からご覧いただけます!
今回も最後までご覧いただきまして、有難うございました。
当サイト、「スマナビング!」では、読者の皆さんのご意見や、記事のリクエストの募集を行なっています。
ご質問・ご意見がございましたら、コメント欄までお寄せください。
お役に立ちましたら、sns等でB!やシェア、Twitterのフォローをしていただけると励みになります。
・その他のお問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。

