空間ベクトルの成分表示と垂直・平行条件をわかりやすく！

ベクトルの成分表示（２）と内積/垂直/平行条件

今回は、ベクトルの成分表示第二回として、「成分表示でのベクトルの足し算・引き算・内積」に引き続いて、ベクトルの内積が《x成分の積 +y成分の積》になる事を導き、それを利用してベクトルの垂直条件と平行条件を学びます。

最後にまとめとして空間ベクトルの(成分表示を使った）応用問題を解いていきます。

また、成分表示を使わない基本的なベクトルの内積については

→「内積がわかる！ベクトル同士の掛け算とは？」をご覧ください。

これまでのベクトルの記事は→「ベクトルとは？0から始める解説記事9選」で復習できます。是非ご覧下さい！

ベクトルの成分表示での内積

※ベクトルの成分表示の基礎は「ベクトルの成分表示と四則演算」で解説しています。

内積が(x1x2+y1y2)になる理由

ベクトルは座標上を動かしても同じ（ベクトルの相等）でしたから、＜図一＞の２つのベクトルの始点を原点Oに合わせて見ます。

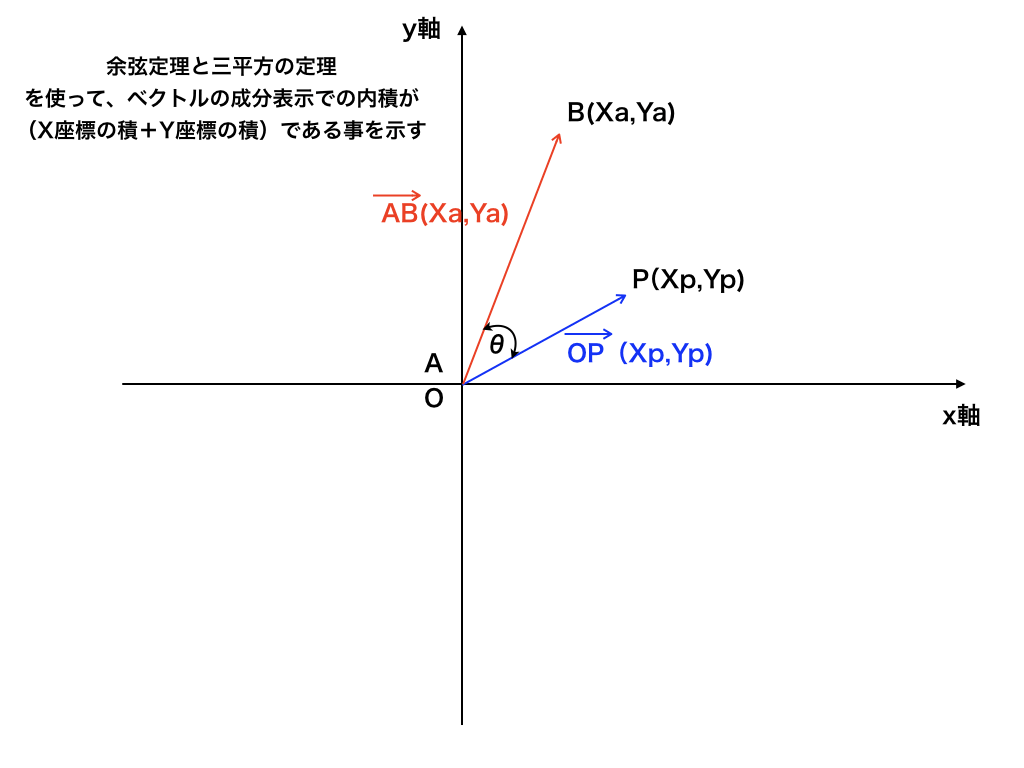
＜図１＞

ここでは、ベクトル\(\vec {OP}=\begin{pmatrix}
x_{p} \\
y_{p}
\end{pmatrix},\vec{AB}=\begin{pmatrix}
x_{a} \\
y_{a}
\end{pmatrix}\)

とします。

（ベクトルの成分は、上に書いたようにタテに並べてもヨコに並べてもどちらでも構いません）

ここで、余弦定理を利用します。

θをなす角とすると、

\((BP) ^{2}=(AB)^{2}+(OP)^{2}-2(AB)(OP) \cos \theta\)

これをベクトルで表すと、

\(AB=|\vec {AB}| ,OP=|\vec {OP}| ,BP=|\vec {BP}|\)

より、\(|\vec {BP}|^{2}=|\vec {AB}|^{2}+|\vec {OP}|^{2}-2|\vec {AB}| \cdot |\vec {OP}| \cos \theta \)

右辺の\(-2| \overrightarrow {AB}| \cdot | \overrightarrow {OP}| \cos \theta\) の部分が、丁度(-2)ABベクトルとOPベクトルの内積になっていますね。

ここで、＜図２＞の様に三平方の定理を利用してBPを求めると、

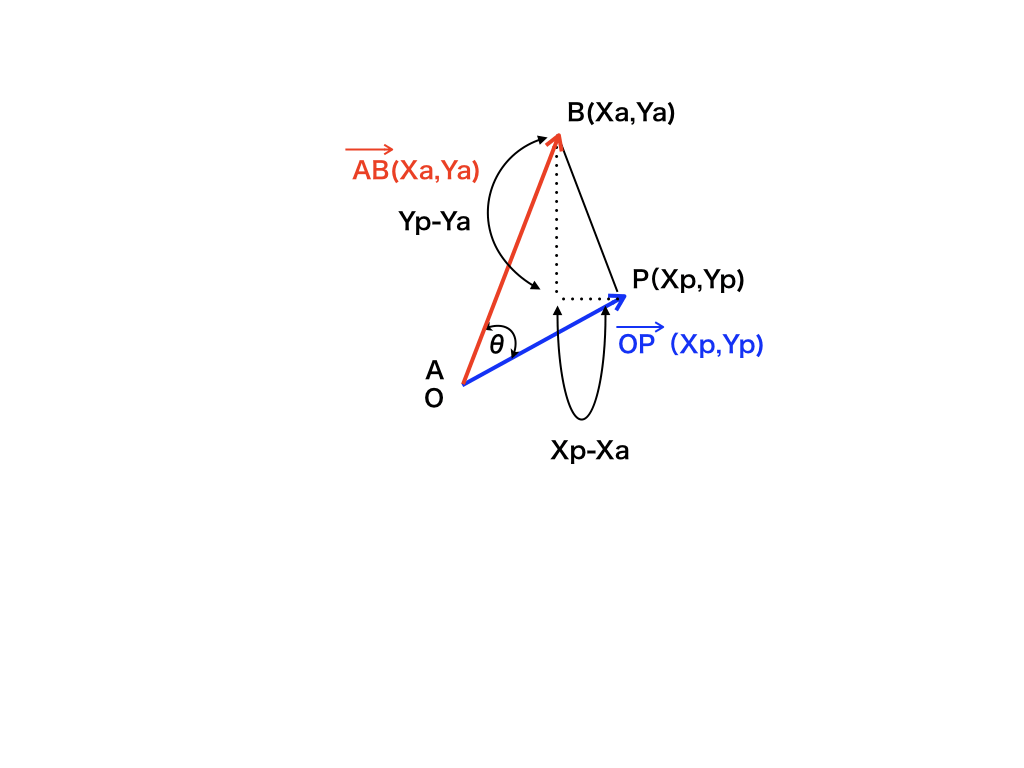
＜図２：成分表示での内積が各成分をかけたものの和になる証明＞

\(| \overrightarrow {BP}|^{2}=( x_{p}-x_{a}) ^{2}+( y_{p}-y_{a}) ^{2}\)

さらに、\(| \overrightarrow {AB}| ^{2}=( x^{2}_{a}+y^{2}_{a})\)

\(|\overrightarrow {OP}|^{2}=( x^{2}_{p}+y^{2}_{p}) \)

上の式を、余弦定理の式に代入して、＜参考：「三角比の意味と表・余弦定理まで一気に習得」＞

\(\begin{aligned}( x_{p}-x_{a})^{2}+( y_{p}-y_{a}) ^{2}\\
=(x^{2}_{a}+x^{2}_{p}) +(y^{2}_{p}+y^{2}_{a}) -2(AB)(OP) \cos\theta \end{aligned}\)

・・・１

ここで、( AB) ( OP) cosθ

\(=| \overrightarrow {AB}| \cdot | \overrightarrow {OP}| \cos\theta\)

\(=\overrightarrow {AB}\cdot \overrightarrow {OP}\)・・・２から、

１式に２式を代入して、整理すると

$$-2x_{a}x_{p}-2y_{a}y_{p}=-2\overrightarrow {AB}\cdot \overrightarrow {OP}$$

よって、確かに\(x_{a}x_{p}+y_{a}y_{p}=\overrightarrow {AB}\cdot \overrightarrow {OP}\)が成立します。

内積の利用と空間ベクトルへの応用

ベクトルの垂直条件と平行条件

ここからは、上で解説した「ベクトルの成分表示での内積」を利用して、

２つのベクトルが垂直になる条件と平行（または重なる）になる条件を紹介します。

ここでは、二本の零ベクトルでない、

\(\vec {a}\begin{pmatrix}
x_{a} \\
y_{a}
\end{pmatrix},\vec {p}\begin{pmatrix}
x_{p} \\
y_{p}
\end{pmatrix}\)を使います。

ベクトルが垂直という事は、二本のベクトルのなす角θが90°だから、内積の式は

\(\vec {a}\cdot \vec {p}=| \vec {a}|| \vec {p}| \cos 90^{\circ }\)

となります。cos90°＝０より

\(\vec {a}\cdot \vec {p}=0\)

すなわち内積が０であれば二本のベクトルは垂直であると言えます。

したがって、成分表示での垂直条件は、\(x_{a}x_{p}+y_{a}y_{p}=0\)

これで、(x成分の積 +y成分の積)＝0 の時、垂直になることが分かりました。

次に、ベクトルの平行条件を考えます

＜図３＞のように、２つのベクトルが平行になる条件は、

\(\vec {u}\neq \vec {0},\vec {v}\neq \vec {0}\)の下で、\(\vec {u}=t\vec {v}\) を満たすtが存在する事です。

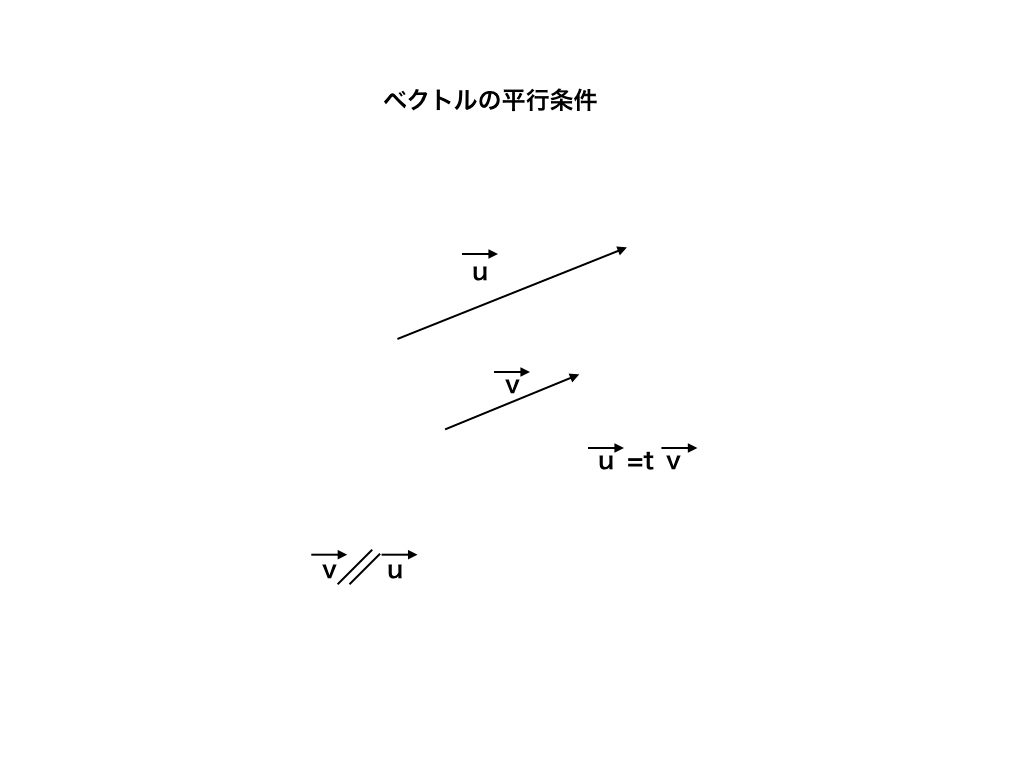
＜図３：ベクトルの並行条件＞

実際にどの様に条件を使うのか、例題で見ていきます。

\(（例題）\vec {u}=\begin{pmatrix}
3 \\
8
\end{pmatrix},\vec {v}=\begin{pmatrix}
2 \\
y
\end{pmatrix}の時、\)

ベクトルuとベクトルvが平行である為のyを求めよ。

\(\begin{pmatrix}
3 \\
8
\end{pmatrix}=t\begin{pmatrix}
2 \\
y
\end{pmatrix}\)

を満たすtとyを探します。

\(\begin{pmatrix}
3 \\
8
\end{pmatrix}=\begin{pmatrix}
2t \\
yt
\end{pmatrix} \)

ここで、x成分、y成分同士を比較して

\(3=2t,8=yt⇔ t=\frac {3}{2},\)

$$従ってy=\frac {16}{3} 、\vec {v}=\begin{pmatrix}
2 \\
\frac {16}{3}
\end{pmatrix}$$

空間ベクトル(3次元)への応用

ここでは、今回学んだことを実践問題を通して身につけていきます。

空間ベクトルの問題なので、成分が（x,y,z)の３つになりますが、

平面ベクトルの場合とする事は同じなので、すぐに慣れるはずです。

問題

xyz空間中に、点A(2,0,0)、点B (0,-1,0)と

ベクトルu:\(\vec {u}=(-1,2,5)、ベクトルv:\vec {v}=(1,1,1)\)

 ベクトルw: \(\vec {w}=(-1,3,1)\)がある。

（１）このとき、\(\overrightarrow {AP}\parallel  \vec{u}かつ　\overrightarrow {BP}\parallel \vec {v}\)となる点P を求めよ

（２）：（１）で求めた点Pに対して、\(\overrightarrow {CP}\bot \vec {w}\)となる点C を求めよ。

（３）：点C、点Pと点A、点Bについて、点Pが平面ABC上にあることを示せ。

解けそうなところまで実際に解いてみてください。

では、解答解説にはいります。

問1:点Pのxyz成分を文字でおいてベクトルの平行条件を使います。

まず点Pの具体的な座標がわからないので、未知数Xp、Yp、Zpを置いて解いていきます。

\(点Pを(x_{p} ,y_{p} ,z_{p})とおく。\)

\vec {AP}=(後)-(前) ：「ベクトルの分解」より

\(=\begin{pmatrix}
x_{p}-2 \\
y_{p}-0 \\
z_{p}-0
\end{pmatrix}=\begin{pmatrix}
x_{p} & -2 \\
y_{p} & \\
z_{p} &
\end{pmatrix}\)

\(\vec {BP}=(後)-(前)\) ：「ベクトルの分解」より

\(\begin{pmatrix}
x_{p}-0 \\
y_{p}-(-1) \\
z_{p}-0
\end{pmatrix}=\begin{pmatrix}
x_{p} \\
y_{p}+1 \\
z_{p}
\end{pmatrix}\)

ここで、実数lとmを置き、「ベクトルの平行条件」より

\(l\vec {u}=\overrightarrow {AP},m\vec {v}=\overrightarrow {BP}\)

これを成分表示であらわすと、

\(l\begin{pmatrix}
-1 \\
2 \\
5
\end{pmatrix}=\begin{pmatrix}
x_{p}-2 \\
y_{p} \\
z_{p}
\end{pmatrix}・・・（※）と、\)

\(m\begin{pmatrix}
1 \\
1 \\
1
\end{pmatrix}=\begin{pmatrix}
x_{p} \\
y_{p}+1\\
z_{p}
\end{pmatrix}・・・（※※）の\)

２式ができるので、x成分y成分z成分の各々の両辺を比較していきます。

（※）より、-l=x_p-2 ・・・(１)

2l=y_p・・・(２)   ,

5l=z_p・・・(３)

（※※）より、m=x_p ・・・(４) 

m=y_p +1・・・(５)   ,

m=z_p・・・(６)

以上より、未知数５個に対して、式が６個できたので必ず解けます。

(４)式と(６)式からx_p=z_p・・・(７)

(７)式を(３)式に代入して、5l=x_p・・・(８)

８式と１式を連立して、\(6l=2 より、l=\frac {1}{3}\)

lの値が求まったので、１、２、７式と\(l=\frac {1}{3}\) から

$$y_{p}=\frac {2}{3} ,z_{p}=\frac {5}{3}$$

$$以上より、求める点Pは、(\frac {5}{3} ,\frac {2}{3} ,\frac {5}{3})$$

問2:垂直条件を利用します

$$点P(\frac {5}{3},\frac {2}{3} ,\frac {5}{3})に対して、$$

\(\overrightarrow {CP}\bot \vec {w}\)となる、点C(0 ,0 ,c)のz成分であるcを求める問題なので、

上で解説した垂直条件＝内積が０を利用します。

\(\overrightarrow {CP}=\begin{pmatrix}
\frac {5}{3} \\
\frac {2}{3} \\
\frac {5}{3}-c
\end{pmatrix}だから、\vec {w}との\)

（x成分＋y成分＋z成分＝０）であれば良いので、

\(\begin{pmatrix}
\frac {5}{3} \\
\frac {2}{3} \\
\frac {5}{3}-c
\end{pmatrix}\cdot \begin{pmatrix}
-1 \\
3 \\
1
\end{pmatrix}=0\)

\(\begin{aligned}⇔ -\frac {5}{3}+2+\frac {5}{3}-c=0\\
c=2\end{aligned}\)

よってc＝２で、点Cを成分表示すると(0 ,0 ,2)となります。

問3:これは係数和1の法則が使えます!!

問3では、「ベクトルとは？0から始める徹底解説９選」でもよく紹介している「係数の和が１」を利用するので、知っている方は解説に進んで下さい。

そうでない人は、次の記事を読んでから、問3の解説を見てください。

「ベクトル問題に必須の『係数和1の法則』が成立する条件と理由」

「ベクトルの共線条件と共面条件とは？」

点PがABCを含む平面上にあることを示すので、点Oから点A,B,C,Pに向けたベクトルが以下のような関係であれば、題意を示せます。

実数g,h,iを置いて\(\begin{aligned}\overrightarrow {OP}=g\overrightarrow {OA}+h\overrightarrow {OB}+i\overrightarrow {OC}\\
( g+h+i=1) \end{aligned}\)

成分で表して、計算していくと

\(\begin{bmatrix}
\frac {5}{3} \\
\frac {2}{3} \\
\frac {5}{3}
\end{bmatrix}=g\begin{bmatrix}
2 \\
0 \\
0
\end{bmatrix}+h\begin{bmatrix}
0 \\
-1 \\
0
\end{bmatrix}+i\begin{bmatrix}
0 \\
0 \\
2
\end{bmatrix}\)

\(\begin{bmatrix}
\frac {5}{3} \\
\frac {2}{3} \\
\frac {5}{3}
\end{bmatrix}=\begin{bmatrix}
2g \\
-h \\
2i
\end{bmatrix}\)

$$g=\frac {5}{6} ,h=\frac {-2}{3} ,i=\frac {5}{6} $$

よってg+h+i=1となるので、点PはABCを含む平面上にある。・・・（証明終わり）

まとめ

・垂直条件:内積＝x成分の積 +y成分の積＝0は「余弦定理」から導く

＜参考：「三角比の意味・表・正弦定理・余弦定理・相互関係をまとめて解説！」＞

・平行条件は、t倍して座標上を動かす(ベクトルの相等)と一致する事を利用する

・空間ベクトルの問題で、平面上にあることを示す時は、「係数の和が1」を利用する。

今回は少しボリュームが多かったかもしれません。

しかし、この記事と前回の「ベクトルの成分表示での足し算引き算掛け算」で基礎部分はかなり固めることができます。

ベクトルの解説記事総まとめ

後は、どんどん問題を解いていきましょう！このベクトルシリーズでも、

更に色々な手法の紹介や、組合せ、発想法などを追加していきます！

・おススメです→【ベクトルとは？ゼロから始める解説記事9選】←を読む！

今回もご覧いただき有難うございました。

質問・記事について・誤植・その他のお問い合わせはコメント欄までお願い致します。

お役に立ちましたら、シェア&当サイト公式Twitter(@linkyjuku_tweet)のフォローをお願いします！