
円順列/じゅず(数珠)順列の解き方と良くあるギモン
この記事をご覧くださっているあなたは「円順列」と「じゅず順列」の違いや、計算する際に『一つ固定』する意味を理解できているでしょうか?
この辺りの分野が曖昧な人はぜひこの記事をじっくり読んでみて下さい!
ちなみに、PとCの違いや順列組み合わせの基礎に自信がなければ、
先に超入門講座(1)→「場合の数と確率超入門講座(1):順列と組み合わせ、PとCの違い」を読む!
目次(タップした所へ飛びます)
円順列とは?
その名の通り、円の様に(主に人など)を並べる順列の事です。
順列があいまいな人は、「順列と組み合わせの違い」をチェック!
普通の順列と円順列の違い
今回一番大事なところです。普通、順列は初めと終わりがあります。
Aさん、Bさん、Cさんを順番に列に並べる場合の数は、
(ABC)、(ACB)、(BAC)、(BCA)、(CAB)、(CBA)となり、
(先頭、真ん中、最後)の6通りあります。
しかし、円順列は「初めも終わりもありません」
例えばに円のテーブルを3人で囲んだ時、先頭の人などいないですよね?
従って、円順列の場合は、簡単に順列の公式
$${}_n P_r$$
が使えません。
円順列の場合の数の求め方
ではどうやって円順列の場合の数を求めるかというと、
「とりあえず、1人を固定して残りの人の順列を考える」という様に習います。
例えば、先ほどの例では、Aさんをテーブルの1箇所に固定して
$$残りのB/Cさんの二人の順列={}_2 P_2$$
$$=\frac{2!}{(2-2)!}=\frac{2!}{0!}=2!$$
よって「2通り」がABCの3人を円状に並べた順列になります。
円順列で「1人固定」する意味
ここは入門記事なので、難しいと感じたら下のじゅず順列へ行ってもらって構いません。
この解法を習った多くの人が“なぜ1人固定する”のか?とギモンに思います。
答えは、「実は固定しなくてもいい」んです。
その代わりに、「固定せずに」解くと、本来『順列は初めと終わりがある』ので、
余計に計算してしまった「重複」分を割る必要が出てきます。
具体的に考えてみましょう。
3人を固定せずに並べる順列は、$${}_3 P_3$$
この中で、同じ並び方をしているものがあります。
(ABC) 、(BCA )、(CAB)の3通りの並び方は、ぐるっとまわすと、(ABC)という1通りの並び方と同じになります。
$$つまり、{}_3 P_3=3!$$の答えは、本来の3倍重複して数えてしまっているのです。
これらを消す為には、3で割らないといけません。
$$結局、\frac{3!}{3}=\frac{3×2×1}{3}=2×1$$
となって、はじめの2!=2通りと同じになります。
これはまだ簡単な円順列なので、固定しなくても重複分をうまく無くせます。
しかし、もう少し難易度が高い円順列の場合にはそれが大変になってきます。
理屈をある程度わかった上で「1人や1個」を「先に固定する」と言う解き方を使える様になりましょう。
(但し、重複円順列と言うものの場合は、違う解き方が必要になります。難易度がグッと上がるので、入門講座が一通り終わった後に紹介します。)
同じものを並べる順列と数珠順列(上)
じゅず順列の前に【同じものを含むものを並べる順列】について解説しておきます。
同じ文字や球を並べる順列
例えば、文字(A,A,A,B,)の4文字があるとき、この文字の並べ方は何通りあるでしょうか。
$$これまでの順列ならば、{}_4 P_4=4!=24(通り)ですが、$$
実際には、3つのAは区別がつきません。(=同じもの)
従って、答えは(AAAB)、(AABA)、(ABAA)、(BAAA)の4通りしかありません。
このように区別のつかないものを並べるとき、重複分を割る便利な解き方があります。
同一のものを並べる順列の公式
n個中k個が同じものを一列に並べる場合の数は
$$\frac {n!}{k!}$$で求めることが出来ます。
先ほどの(A,A,A,B)の場合は4個中3個が同じAだったので
$$\frac {4!}{3!}=\frac {4×3× 2×1}{3×2×1}=4$$で求めることが出来ます。
この公式が成り立つ理由
さて、同じものの順列が$$\frac{n!}{k!}$$で良い理由を知っておきましょう。
(A,A,A,B)は、上の公式に従うと$$\frac{4!}{3!}=4となります。$$
ここで、仮に3つのAにそれぞれ区別がつく様に、添え字を付けてみます。
$$(A_{1},A_{2},A_{3},B)この4文字の順列は、4!=24$$
しかしながら実際には区別がつかないので、重複分を減らす必要があります。
(A1,A2,A3,B)
,(A1,A3,A2,B),
(A2,A1,A3,B)
(A2,A3,A1,B),
(A3,A1,A2,B),
(A3,A2,A1,B)
の6つは(A,A,A,B)の一通りにまとめられます。
つまり、A1、A2、A3の並べ方である「3!=6通り」より、六倍多く数えてしまっているので、
$$4!で3!を割る⇔\frac{4!}{3!}$$
これが、同じもの(や同じ文字を)並べる公式の意味です。
ちなみに、この考え方を応用することで「二項定理・多項定理の係数を求める公式」(←解説記事です)も理解できます。
数珠(じゅず)順列
じゅず順列は円順列の親戚の様なものですが、少し異なっている部分があります。
この項では、そのじゅず順列の基礎を学びます。
円順列とじゅず順列の違い
じゅず順列は、円順列と異なり裏側から見て同じ並び方のものは同一として数えます。
こちらも具体的に考えていきます。
じゅず順列の例
今青色の球一個と黒色の球二個と赤色の球3個がある。
この6つの球に糸を通して数珠(ネックレスでもなんでも良いです)を作る時の場合の数を求めよ。
これが普通の円状に配置せよという円順列ならば、青色の球一個を固定して、$$\frac{5!}{3!2!}=10通り$$
で正解なのですが、今回は数珠を作らないといけないのでこの解法は使えません。
数珠順列の公式
一応公式を書きますが、必ず意味を理解して使う様にしましょう。
$$\frac{円順列の場合の数ー左右対称な場合の数}{2}+ 左右対称な場合の数$$
<図2>に円順列の10通りを書き出しました。
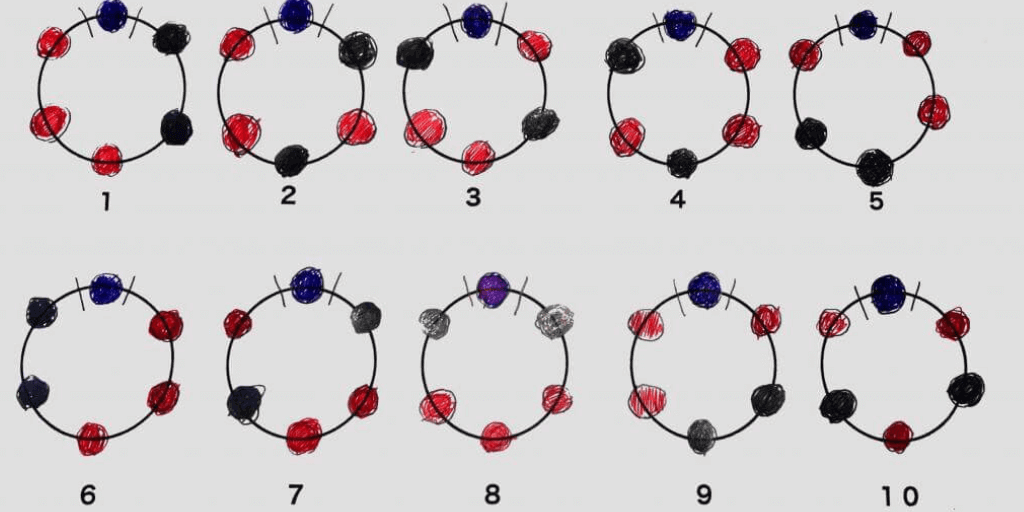
<図2:数珠順列の全通り書き出し>
この内、8 と 10は 左右対称で裏返しても同じになります。
次に、(1と6)、(2と4)、(3と7)、(5と9)、の4組は各組みは対称ではありませんが、数珠順列では同じものとみなします。
そこで、円順列の場合の数からこの2通りを先に引いた数を2で割って、後から左右対称な2通りを足す事でじゅず順列の場合の数が求められます。
$$単純に\frac{円順列の全通り}{2} $$
と覚えてしまっている人がいますが、少し難しい問題になると即間違えるので要注意です。
円・数珠順列のまとめ +次回予告
次回の場合の数と確率超入門講座は、同じ文字の並べ方や、いくつかの数字を選んで◯桁の数字を作ると言う様な典型問題を解説して行きます。↓
続編「◯桁の整数や偶数を作る場合の数の解法」を読む。
「場合の数と確率を得意分野にする!解法解説総まとめ」←重要な問題や解法をまとめました。
今回も最後までご覧いただき有難うございました。
お役に立ちましたら、シェア&当サイト公式Twitter(@linkyjuku_tweet)のフォローをお願いします!
質問・記事について・誤植・その他のお問い合わせはコメント欄、又はお問い合わせページまでお願い致します!

