行列式の定義式と互換・置換をできるだけわかりやすく!
<この記事の内容>:一見難解な『n次行列式の定義式』を読み解くために、『置換・互換』や『sgn』など定義式を一つ一つ分解して解説していきます。
定義式の理解の準備に『置換・互換』(群論と呼ばれる分野)や『集合・写像』を理解する必要があるなど、少々大変ですが一度理解すると、行列式の基本操作の証明などが行えるのでぜひ頑張って取り組みましょう。
<定義式の確認をしたい方は→>:「行列式の定義式・性質と求め方」
<集合と写像(単射・全射・全単射)の確認→>:「写像とは?集合と全単射を解説」
目次(タップした所へ飛びます)
行列式の定義式
まずはじめにこれから攻略する『n次行列式』の定義となる式を書いておきます。
本などによって多少書き方は異なる場合がありますが、意味はどれも同じです。
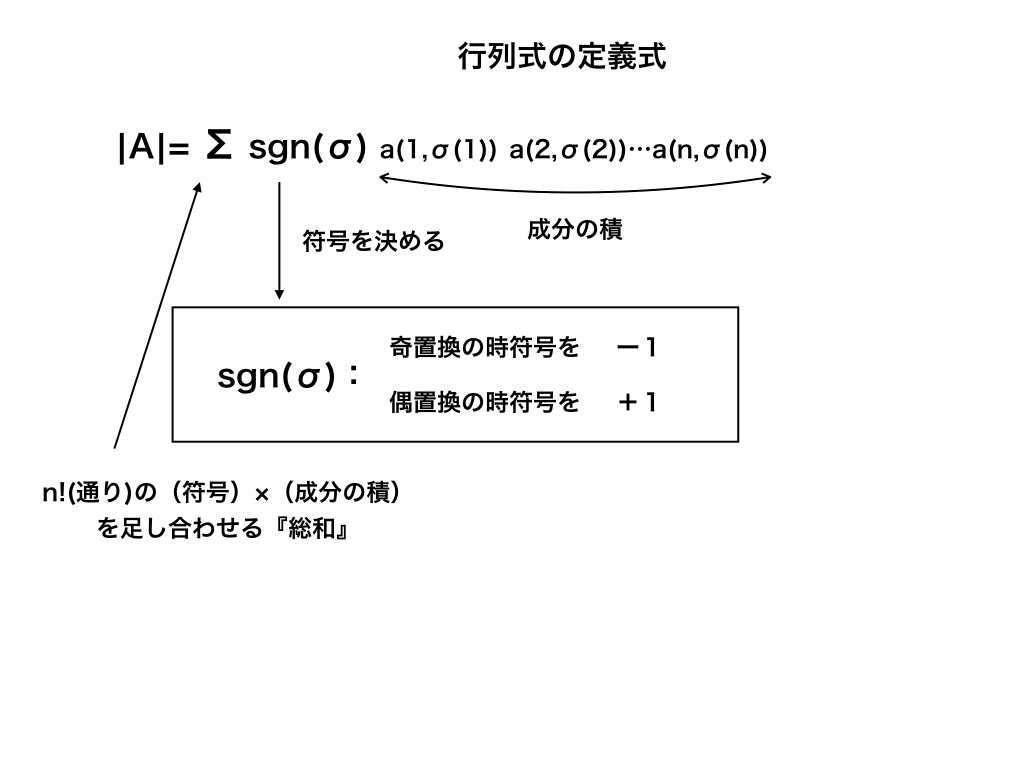
$$\left| A\right| =\sum _{\sigma \in S_{n}}( sgn\left( \sigma \right) \prod ^{n}_{i=1}a_{(i,\sigma _{i})})$$
総和・『sgn』・総乗記号、などなど暗号のように見えます。
sgnって何?
とりあえず、見慣れない『sgn』について、sgnはsignature(符号)という意味です。2次の行列式は行列$$\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}$$に対して、ad-bcで求めることができました。
また、3次の行列式は『サラスの公式』より
$$\begin{bmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{bmatrix}$$
について、 aei+bfg+chd-ceg-ahf-bdi で求まりました。
つまりこの『sgn=符号』とは各成分の積のまえに付く±1のことを意味します。このことについて詳しくは、その次の記号『σ』とともに紹介します。
置換の記号σと写像
この記号はσ(ギリシャ語のΣの小文字)ですが、「置換」を意味します。
置換とは一体なんなのでしょうか?
簡単に言うと、上段のn個の自然数(1からnまで)の集合を、同じ集合である下段の自然数(同じく1〜n)を1対1に写したものです。
(集合と写像については右の記事を参考にしてみてください「単射・全射・全単射とは?集合と写像」で解説している『全単射』に当たります)
例えば、n=2の時、
$$σ=\begin{pmatrix}
1 & 2 \\
2 & 1
\end{pmatrix},\begin{pmatrix}
1 & 2 \\
1 & 2
\end{pmatrix}$$
のように表し、
・左側の置換は”上段の1を下段の2”、”上段の2を下段の1に写しており、
・右側の置換は”上段の1と下段の1”、”上段の2と下段の2を写しています。
また、置換の各数を一般に以下のように表します。
$$\begin{pmatrix}
1 & 2 & \ldots & n & \\
\sigma (1) & \sigma(2) & \ldots & \sigma(n)
\end{pmatrix}$$
n=3,4,5・・・と増えるにつれて置換の数がn!(nの階乗個)に増えていきます。
これは『違うものをn個並べる順列』の問題と同じなので理解しやすいのではないでしょうか。
恒等置換
さて、先ほどのn=2での置換のうち、右側の置換は上段の数と下段の数が一致していました。
このような置換のことを特別に『恒等置換』と呼びます。以下に、n=3,4の時の恒等置換を例示しておきます。
n=3 n=4
$$\begin{pmatrix}
1 & 2 & 3 \\
1 & 2 & 3
\end{pmatrix},\begin{pmatrix}
1 & 2 & 3 & 4 \\
1 & 2 & 3 & 4
\end{pmatrix}$$
これらの恒等置換は、のちに解説する『互換』・そして『sgn』と関連して行列式の符号を決める重要な要素となります。
互換とは何か
互換とはその文字通り『互いに(数)を交換』することを言います。
例えば、$$\begin{pmatrix}
1 & 2 & 3 & 4 \\
2 & 4 & 1 & 3
\end{pmatrix}$$の置換があったとします。
この置換の成分のうち、一番左の列の上段1に対して、対応している自然数は2です。
これをσ(1)=2といった風に表します。
同様に、σ(2)=4,σ(3)=1,σ(4)=3と表すことができます。
偶置換と奇置換
ここで、『恒等置換から上で例示した置換まで』互換を繰り返してみます。
$$\begin{pmatrix}
1 & 2 & 3 & 4 \\
1 & 2 & 3 & 4
\end{pmatrix}$$
σ(3)とσ(4)を入れ替えます。
$$\begin{pmatrix}
1 & 2 & 3 & 4 \\
1 & 2 & 4 & 3
\end{pmatrix}$$
つぎに、σ(1)とσ(2)を入れ替え、
$$\begin{pmatrix}
1 & 2 & 3 & 4 \\
2 & 1 & 4 & 3
\end{pmatrix}$$
さらに、σ(2)とσ(3)を入れ替えます。
$$\begin{pmatrix}
1 & 2 & 3 & 4 \\
2 & 4 & 1 & 3
\end{pmatrix}$$
このように、操作を『恒等置換』から『選んだ組みの置換』になるまで繰り返しおこなったとき、
・その互換の回数(置換の積の回数)が偶数の場合は『偶置換』
・奇数の場合のことを『奇置換』と呼びます。
今回の例では、恒等置換から”3回互換を行った”ので、『”奇”置換』です。
あともう少しで行列式の定義式の意味がわかります。
sgnσの謎を解き明かす
もう一度定義式を見てみると、
$$\left| A\right| =\sum _{\sigma \in S_{n}}( sgn\left( \sigma \right) \prod ^{n}_{i=1}a_{(i,\sigma _{i})})$$
Σの意味は、文字通り総和です。
ここで、相乗記号Πを外して、sgn(σ)以降の部分をもう少しわかりやすくしてみましょう。
$$( sgn( \sigma) a_{(1,\sigma _{1})}\times a_{(2,\sigma _{2})}\ldots \times a_{(n,\sigma _{n})})$$
行列の各成分である$$a_{1,\sigma_{1}},\ldots,a_{n,\sigma_{n}}$$の部分に注目すると、成分の行番号が置換σの上段、列番号がσ (番号)より置換の下段に対応していることが分かります。
sgn(σ)と互換の回数が符号を決定する。
恒等置換からある組まで互換する回数が奇数の時、sgn(σ)は−1・偶数の時は+1と「成分の積」の符号を決定します。(上述した偶置換・奇置換)
これだけでは抽象的なので、3×3サイズの行列の行列式を上の定義式と対応させながら見ていきます。

$$\begin{bmatrix}
a_{1,1} & a_{1,2}& a_{1,3}\\
a_{2,1} & a_{2,2}& a_{2,3}\\
a_{3,1} & a_{3,2}& a_{3,3}
\end{bmatrix}$$
まず、n!の数だけ置換があり、それぞれの成分はある行から1つ、ある列から1つ重複せずに組み合わせたものです。
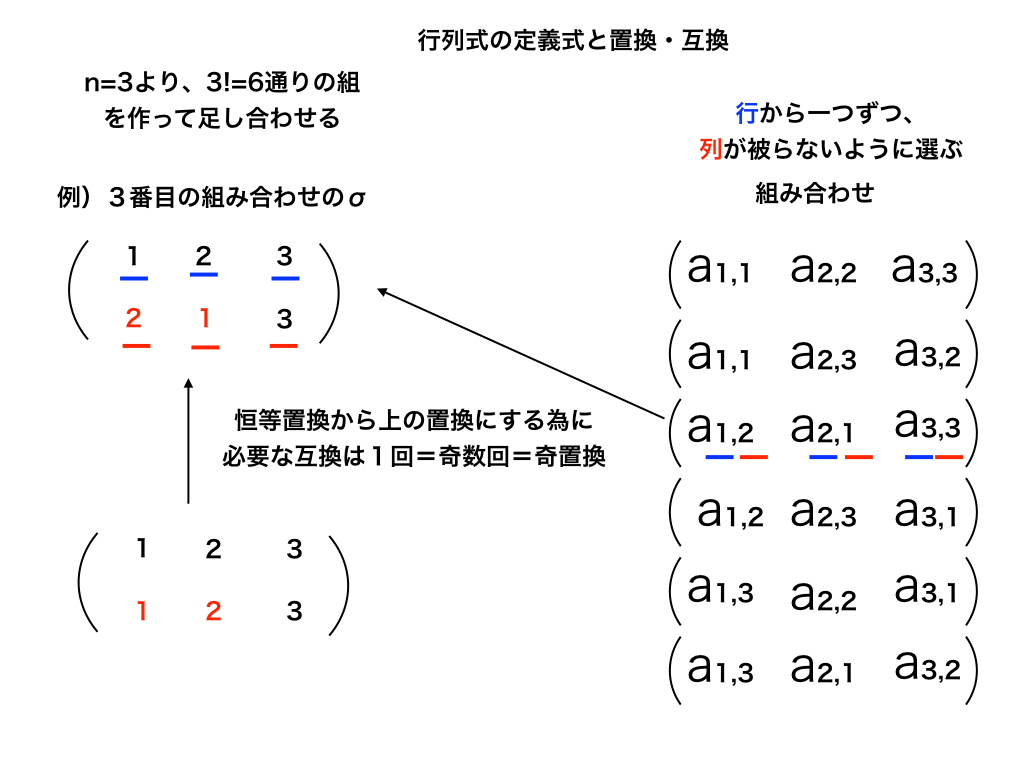
今回はn=3より6通りの組みから、$$(a_{1,2},a_{2,1}, a_{3,3}$$の組みを例として取り上げます。
上図のように、行列の成分を置換の上段と下段に対応させて『偶置換』か『奇置換』かを調べます。
今回は奇置換なので、符号はマイナスになり、それを行列の成分とかけあわせます。

この計算を1番目〜6番目まで3番目と同様に行って足し合わせます。(n=3の場合)
(練習として、3番目以外の1、2、4、5、6番目の組みの符号を調べて、各成分と掛け合わしたものを全て足してみてください。サラスの公式と同じ結果が導けます!)
これが、n次の行列式の定義式の意味です。
<練習の答え3×3の行列式>
$$sgn\begin{pmatrix}
1 & 2 & 3 \\
1 & 2 & 3
\end{pmatrix}a_{11}a_{22}a_{33}$$
$$+sgn\begin{pmatrix}
1 & 2 & 3 \\
1 & 3 & 2
\end{pmatrix}a_{11}a_{23}a_{32}$$
$$+sgn\begin{pmatrix}
1 & 2 & 3 \\
2 & 1 & 3
\end{pmatrix}a_{12}a_{21}a_{33}$$
$$+sgn\begin{pmatrix}
1 & 2 & 3 \\
2 & 3 & 1
\end{pmatrix}a_{12}a_{23}a_{31}$$
$$+sgn\begin{pmatrix}
1 & 2 & 3 \\
3 & 2 & 1
\end{pmatrix}a_{13}a_{22}a_{31}$$
$$+sgn\begin{pmatrix}
1 & 2 & 3 \\
3 & 1 & 2
\end{pmatrix}a_{13}a_{21}a_{32}$$
それぞれの符号を調べて、成分の積の和の形にすると、
$$a11a22a33+(-1)a11a23a32$$
$$+(-1)a12a21a33+a12a23a31$$
$$+(-1)a13a22a31+a13a21a32$$
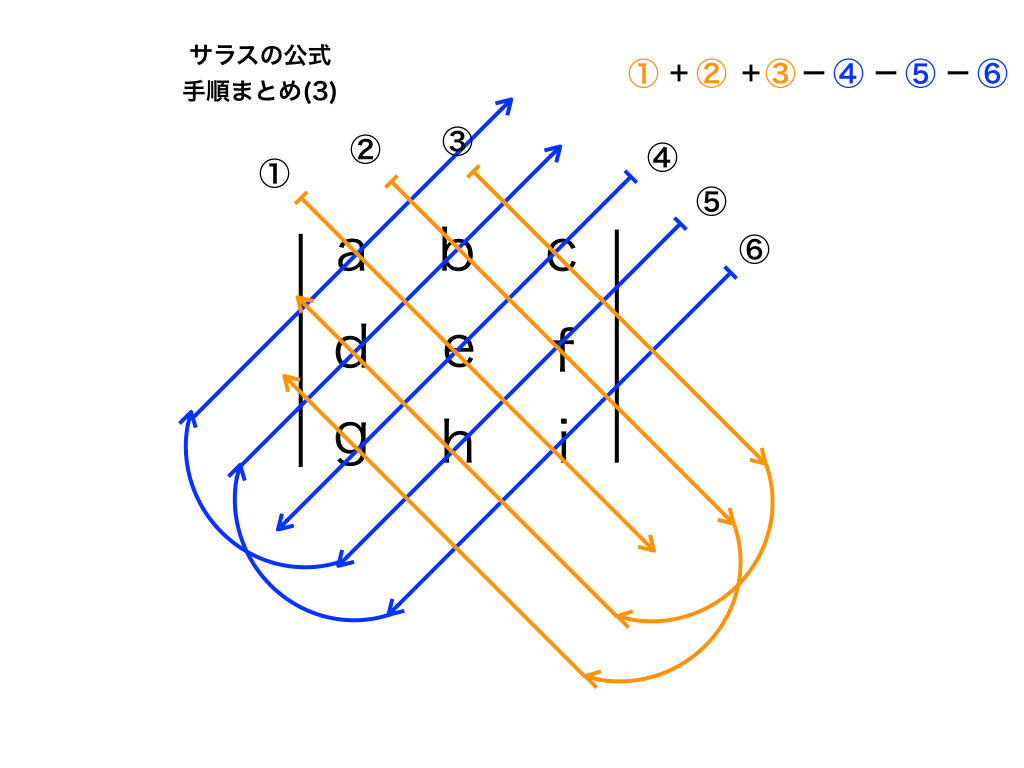
きちんと「サラスの公式」と同じになっています。
まとめと置換・互換から行列式の性質の証明へ
かなり大変でしたが、一旦この定義式の意味を理解すると、行列式の性質(例えば【行を入れ替えると行列式の値がマイナスになる】など)を全て証明することができます。
(行を入れ替えると互換の回数が1回増える→奇置換なら偶置換に、偶置換なら奇置換に変化するので符号が逆転するからです)
ぜひ何度も復習してマスターしましょう!
線形代数:関連記事一覧
今回も最後までご覧いただき、有難うございました。
「スマナビング!」では、読者の皆さんのご意見や、記事のリクエストの募集を行なっています。
ご質問・ご意見がございましたら、ぜひコメント欄にお寄せください。
またいいね!やB!、シェア、をしていただけると励みになります。
・その他のお問い合わせ/ご依頼などに付きましては、お問い合わせページからご連絡下さい。