ニュートンリングと回折格子の問題でチェックするたった2つの事とは?

光波の干渉実験（２）：回折格子とニュートンリング

 

この記事は「光波の干渉実験（１）重要なことは２つだけ」の続編です。

前回は、干渉実験のうち
・「ヤングの二重スリット実験」、「薄膜による干渉実験」、「くさび形空気層実験」を解説しました。

今回は、前半で前回説明しきれなかった
・「回折格子」と「ニュートンリング」の解説を行い、後半では光の波長と可視光線の関係を紹介します。

（ニュートンリングの説明→光の波長と可視光線→回折格子の説明→次回の実践問題の準備、の順で解説していきます。）

ニュートンリングの仕組み

「光路差」「位相」と波長の比較が全て

今回も実験装置は変わりますが、「光路差（行路差×屈折率）」と「位相のずれ」をの2つをチェックして、

光の波長λと比べる事がほぼ全てであることに変わりありません。

詳しくは＞＞「光波の干渉実験１：ヤングの実験・くさび形・薄膜干渉の解説」＜＜

また、近似の考え方も重要です。

・xの大きさが1よりはるかに小さい時、

「(1+x)ⁿ≒1+nx」

・θが限りなくゼロに近い時、「sinθ≒tanθ」

の近似が成り立ちます。（高校物理では、難易度が上がるにつれて近似の重要性が増してくるので、

早いうちに身につけておきましょう！）

ニュートンリングとは

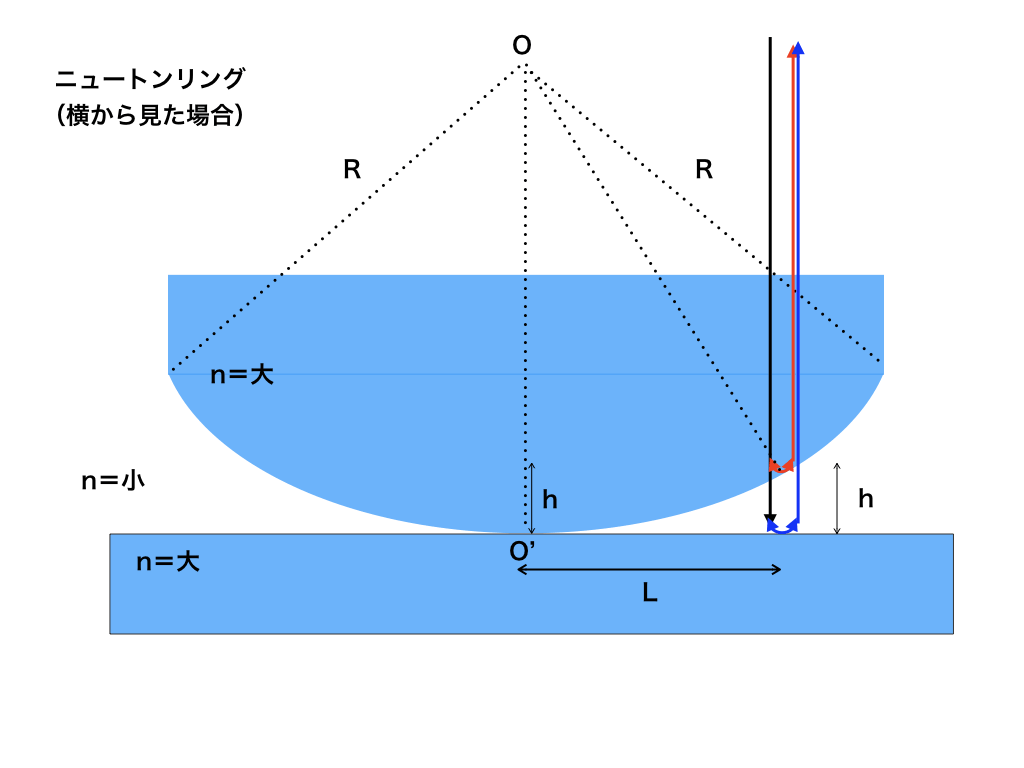
ニュートンリングは＜図１＞の様な形をしたものです。

＜図１：ニュートンリング＞

＜図１＞は横からニュートンリングを見たもので、半径Rの円の一部が同じ屈折率でできた台の上に乗っている装置です。

ニュートンリングを上から見ると。明るい輪と暗い輪が交互に並んでいます。

このそれぞれの輪の中心をOとして、その位置から距離:L離れたところで起きる光の干渉をみてみます。

かのニュートンが発見した装置で輪＝リングが見えるので、ニュートンリングと呼ばれています。

（実際には、同時期の科学者フックが発見したという説が有力です。当時ニュートンとフックは、激しいライバル関係にありました）

位相のチェック

・今赤で描いた光は屈折率大→小の所で反射しているので、位相はずれません。

・一方、青で描いた光は屈折率小→大で反射しており、位相がπずれます。

光路差のチェック

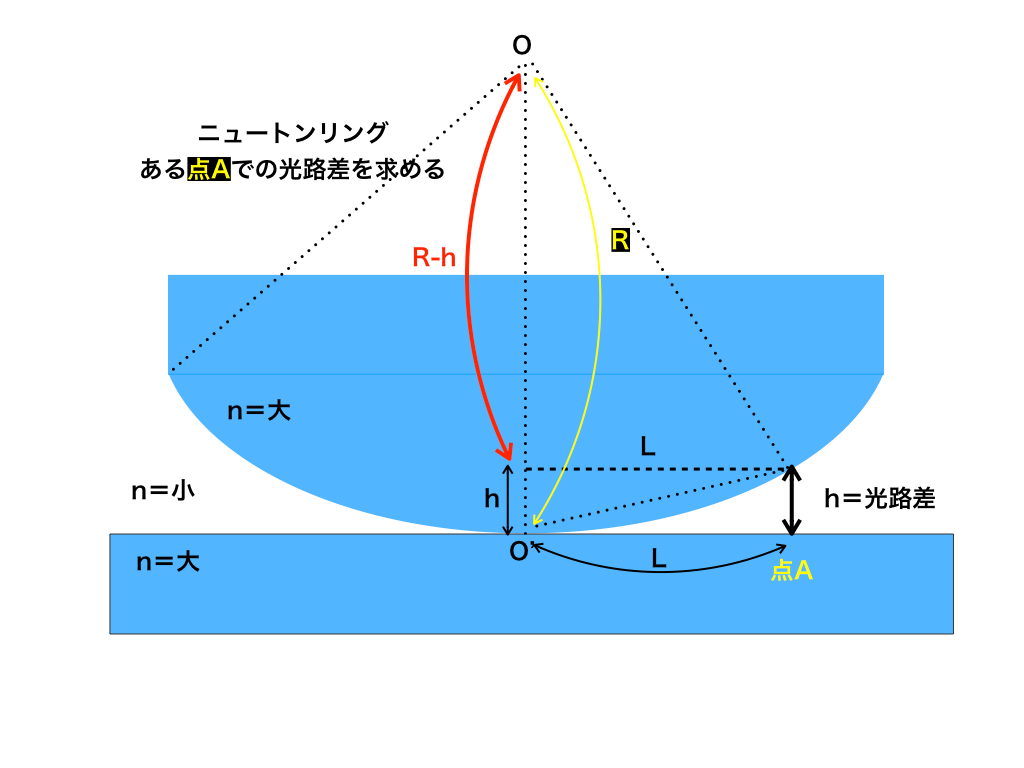
まず、ニュートンリングを横からみた＜図1＞のOからL離れた位置（点Aとします）での光路差（の片道分）をhと置いて計算してみましょう。

＜図：ニュートンリングの光路差をチェック＞

ピタゴラス(三平方)の定理より、３辺の長さが（R-h)、R、Lの三角形に注目して、

\((R-h)^{2}+L^{2}=R^{2}\)

\(⇔R^{2}-2Rh+h^{2}+L^{2}=R^{2}⇔-2Rh+h^{2}=-L^{2}\)

ここで、近似を利用します。R≫hより、h²は非常に小さくなる為無視します。

よって、⇔2Rh=L²

求めたいのは光路差(の片道分)hだったので、

$$h=\frac{L^{2}}{2R}$$

原点からの距離と明線/暗線の関係を調べてみよう

光路差が求まったので、これを利用して、中心Oからどの位の距離に明線・暗線が現れるかを調べます。

ニュートンリングは位相が一回ズレているので、

明線条件は(光路差)＝{mー(1/2)}λ、暗線条件は(光路差)＝mλ、(それぞれm=1,2,3,,,)でした。

$$mλ =2×h=2× \frac {L^{2}}{2R}$$

$$⇔mλ =\frac {L^{2}}{R}⇔ L^{2}=mRλ $$

よって、暗線が現れる（暗く見えている輪の部分の中心からの距離L＝）原点からの距離の条件Lは、

$$L=\sqrt {mR\lambda}$$

一方明線条件より、

$$( m-\frac {1}{2}) λ =2h=2×\frac {L^{2}}{2R}=\frac {L^{2}}{R}$$

$$⇔( m-\frac {1}{2}) Rλ =L^{2}$$

よって、明線が現れる（明るく見えている輪の部分の中心からの距離L＝）原点からの距離の条件Lは、

$$L=\sqrt {( m-\frac {1}{2}) Rλ }$$

であることがみちびけます。

輪の間隔が狭くなっていく事を式とグラフで確認する

『輪の間隔は原点から離れるにつれて、段々と狭くなっていく』事はよく知られていますが、そのことを暗線条件を使って確認しておきましょう。

まず、輪の間隔がm+1番目の暗線条件:L_m+1＝√(m+1)Rλから、m番目の暗線条件:L_m=√(m)Rλを引いたものであることに注目します。

この式のうち、Rとλは一定であるのに対して、√mの値のみ変化することより、輪の間隔は隣り合う√mの数値によってのみ変化することがわかります。

ここで、y＝√mの関数のグラフを見てみましょう。

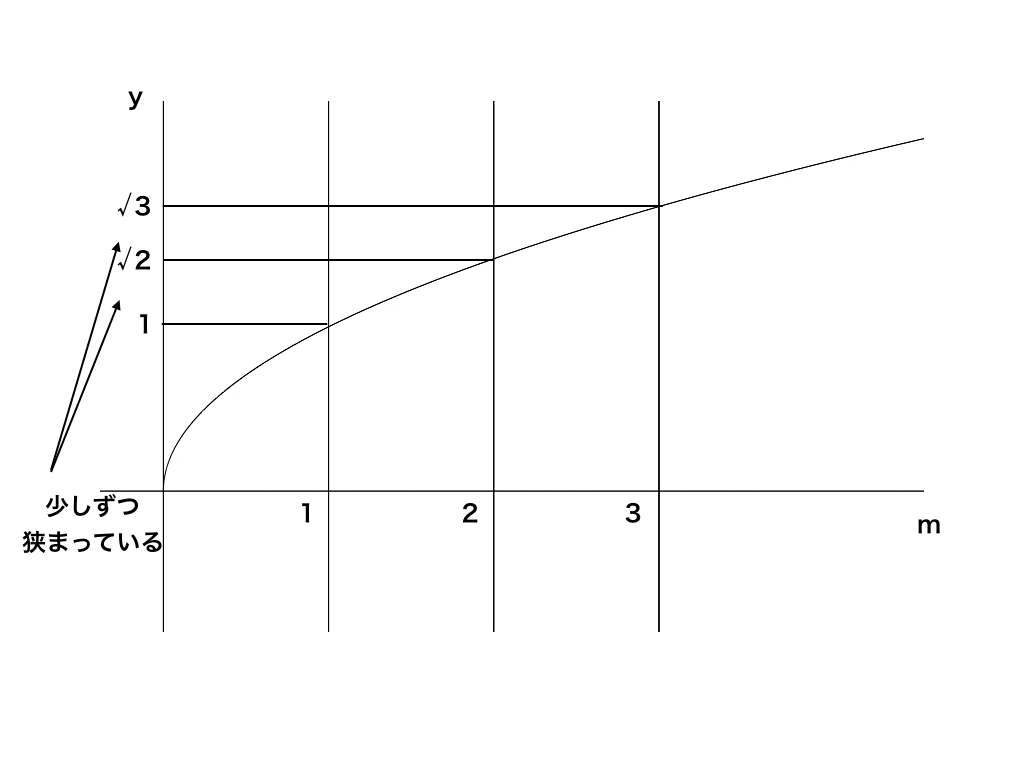
y＝１,√2,√3,・・・とmの値が大きくなるにつれて”yの値の変化量が小さくなっている”ことが確認できます。

つまり、係数部分である√mが無理関数（実際は連続ではないので関数ではないですが）であるので、輪の間隔は徐々に狭まっていくのです。（もし、√が付いていなければ（y＝m）間隔は等しくなる）

実際の数字を入れてみると、

\(暗線条件：L=\sqrt {mR\lambda}\)より、

mに１、２、３・・・と代入していきます。（原点から1番目の暗い輪・2番目の暗い輪・3番目の・・・）

\(L_{1}=\sqrt {1×Rλ}=\sqrt {Rλ}\)

\(L_{2}=\sqrt {2×Rλ}=\sqrt {2Rλ}\)

ここで√ 2≒1.414とすると、

L₂=1.414Rλ

\(L_{3}=\sqrt {3\times Rλ}=\sqrt {3R\lambda}\)

ここで、√3≒1.732とすると、

L₃=1.732Rλとなります。

さらに、L₁とL₂とL₃間の距離＝間隔を計算すると、

L_１とL₂の間隔＝(1.414-1)Rλ＝0.414Rλ

L₂とL₃の間隔＝(1.732-1.414)Rλ＝0.318Rλ

と確かに間隔が狭まっている事が数式で確認できました。

光の波長と可視光線

ここからは、単に明線・暗線条件を求めるだけではない、「色」に関しての問題に対応するために、光の波長と可視光線の範囲について解説します。

光波の波長

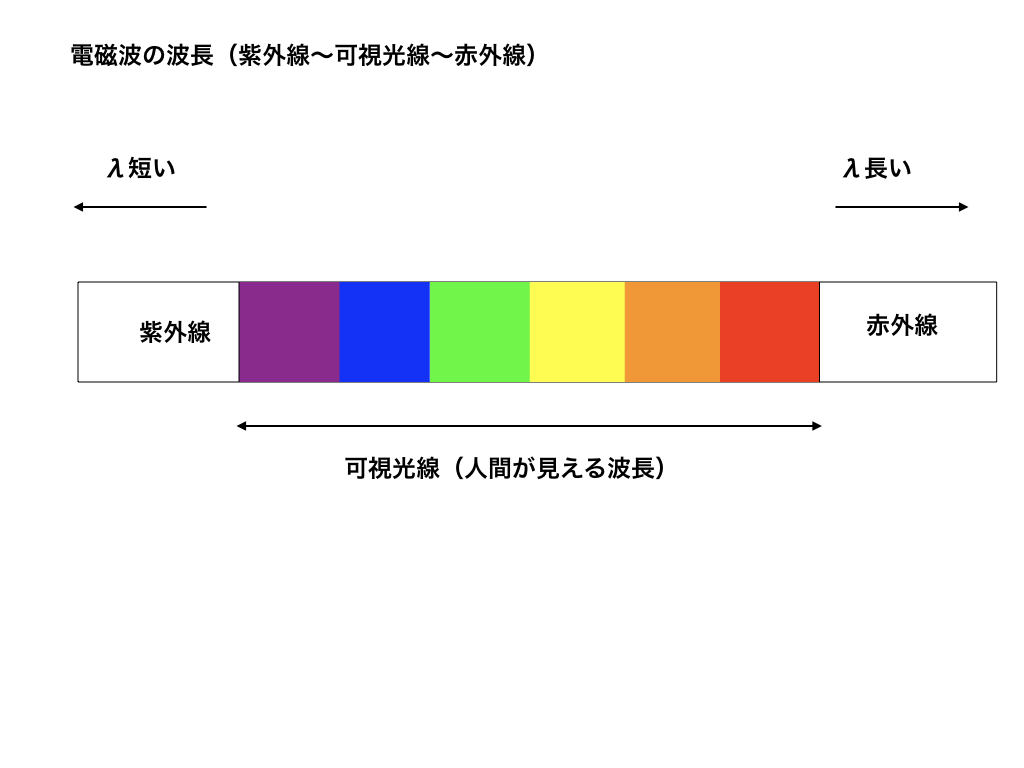
今後光の干渉の問題を解くときに、可視光線の波長の範囲や色の順番を知っていることが前提としたものが出てきます。

(光波)は電磁波の一部で、波長λが長い方から(赤外線)＞赤＞橙＞黄＞緑＞青＞紫＞(紫外線)

具体的にはλ＝780（nm）が可視光線で最大(赤色)〜λ＝380（nm）で最短(紫)の幅は覚えておきましょう。

nはナノ（10^-9)を表す単位です。

波長λが大体780nmを超えると「赤外線」、λ＝380nmよりも短くなると「紫外線」となり

可視光で無くなります（人間が見ることが出来なくなります）。

回折格子の仕組み

回折格子は、ものすごく細かなスリット(切り込み)が無数に入っている装置です。

この切り込みの間隔を格子定数と言いdで表します。

回折格子にもいろいろな種類がありますが、一般的に高校範囲(大学入試)では＜図4＞の様な「透過型回折格子」をメインで扱います。

＜図４：透過型回折格子の例＞

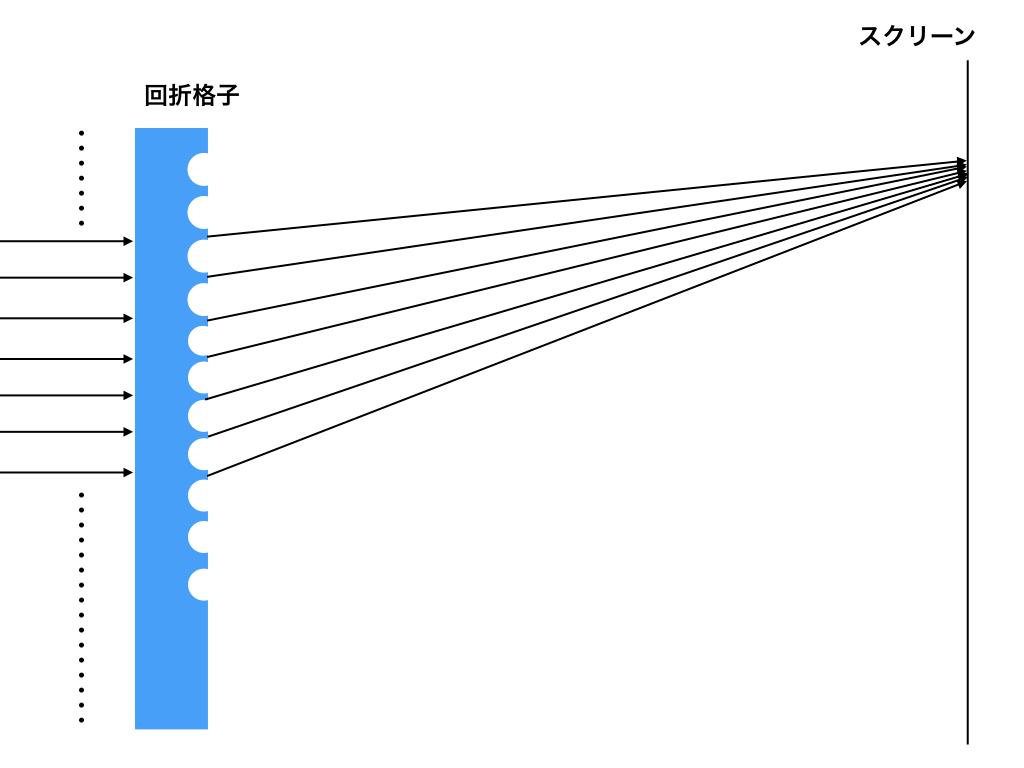
そこにレーザー光を当てると一つ一つのスリットから屈折した光波が出てきます。＜図5(イメージ)＞

＜図5＞

実施には、上図５の様にθ向きだけでなく、あらゆる方向に光は進みます。

その結果として、以下の光路差と位相の条件

(明線条件dsinθ＝mλ、暗線条件dsinθ＝(m-1/2)λ、但しmを0、±1 ±2 ...とする)が、

先ほど解説した可視光線の波長を満たす場所が明るく見えるのです。

位相と光路差のチェック

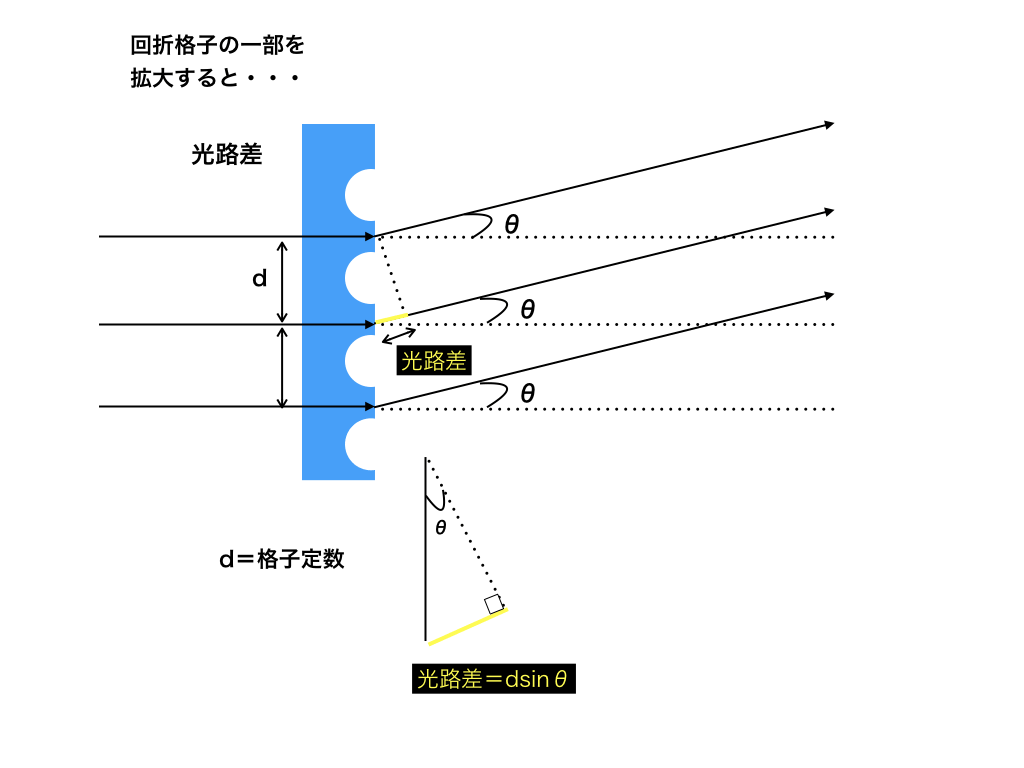
では、回折格子の位相と光路差のチェックをしていきます。

位相のチェック

位相のズレはありません。

光路差のチェック

光路差は、＜図３＞の黄色の線の部分です。ここで光路差を計算すると、dsinθが光路差になっています。

よって、上でも少し書きましたが、

・明線条件は、mλ＝dsinθ

・暗線条件は、(m-1/2)λ＝dsinθ

（それぞれm＝0、±1 ,±2 ...）

となります。

まとめと波動関連記事

・今回はニュートンリングと回折格子の基本を扱いましたが、基本的にやる事は光路差と位相のチェックで以前と同じです。

次回は、「薄膜による干渉」・「くさび形空気層実験」・「ヤングの二重スリット実験」の応用的な問題を解いていきます。

・光波第１回：「光波の干渉実験(二重スリット・薄膜・くさび形空気層)」

・光波第２回：「今ココ」

・光波第３回：(製作中)「実際にどんな問題が出題されるのか、実践問題を解説」

 

今回も最後までご覧いただき、有難うございました。

お役に立ちましたら、シェア&当サイト「スマホで学ぶサイト、スマナビング！」公式Twitterのフォローをお願いします！

質問、誤植はコメント欄、その他のお問い合わせ・ご依頼等はお問い合わせページからお願い致します。