行列同士の掛け算
前回「線形代数入門(1):行列の基礎」の続編です。今回は、行列の掛け算を解説していきます。
線形代数の最初の壁ですが、その分イラストを豊富に使用して丁寧に解説しています。
付録の例題を実際に手を動かして解いてもらえれば、
必ずできる様になるので、ぜひじっくり読んで攻略してしまいましょう!
目次(タップした所へ飛びます)
行列の掛け算のルール
さて、行列の掛け算にはいくつかルールがあります。
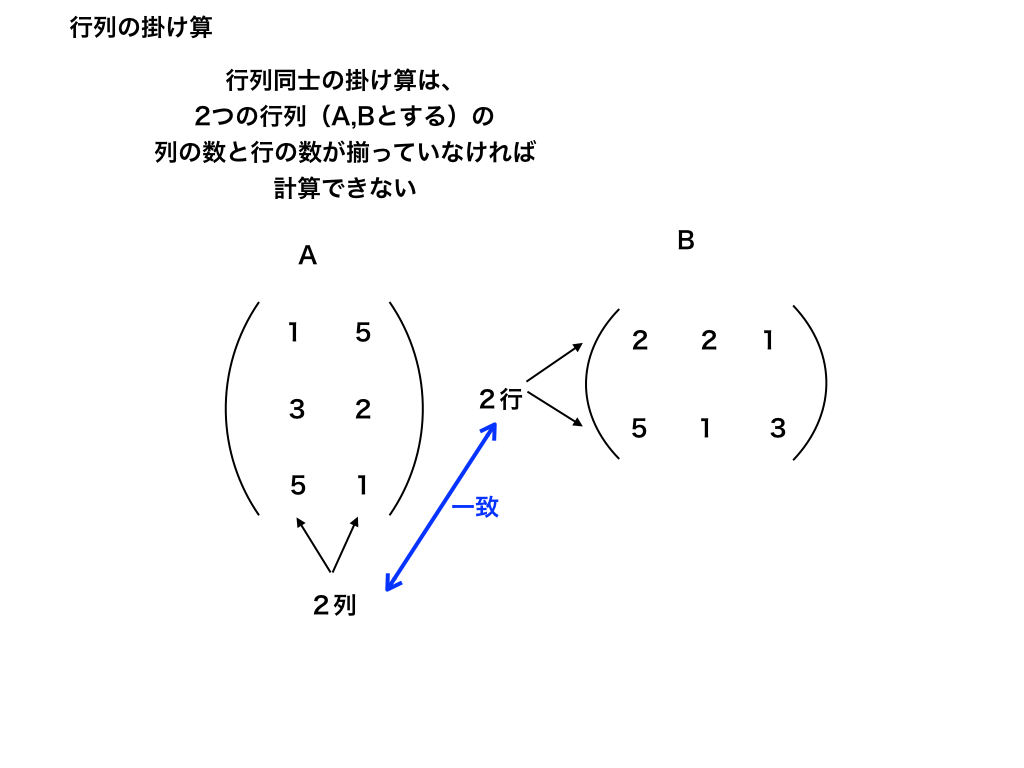
行と列の数が同じである事
1つは、<図>の様に、掛け合わせる2つの行列の、片方の列数ともう片方の行数が揃っていなければいけない、と言うことです。
(両方、つまり行の数も列の数も揃っていなければならないと言う訳ではありません。)
<図:行列の積のルール>
かける順番で結果が変わる(非可換)事
次に、掛け算の順番によって結果が変わる、ということです。
これまでの数学・算数では2×7も7×2も同じ答え14になりました。
この様に順番を入れ替えても成立することを「可換」と言います。
しかし、行列の世界ではほとんどの場合(*)この法則が成り立たず(非可換と言います)AB≠BAとなります。
【関連記事:「ベクトルの外積とは?ベクトルどうしのもう一つのかけ算」】
このことについては、以下の行列の手順の後に実例を挙げて紹介していきます。
(*)この事についても後述します。
ではさっそく行列の掛け算の手順を見ていきましょう。
行列の掛け算の手順
実際に、3×2の行列Aと2×3の行列Bの掛け算の手順をイラストを使って一歩一歩見ていきます。
出来れば、手元にペンと紙を用意してイラストの通りに書き写しながらご覧ください。
行列の積の計算手順
$$行列A=\begin{pmatrix}
1 & 5 \\
3 & 2 \\
5 & 1
\end{pmatrix},行列B=\begin{pmatrix}
2 & 2 & 1 \\
5 & 1 & 3
\end{pmatrix}$$
$$AB=\begin{pmatrix}
1 & 5 \\
3 & 2 \\
5 & 1
\end{pmatrix}\begin{pmatrix}
2 & 2 & 1 \\
5 & 1 & 3
\end{pmatrix}$$
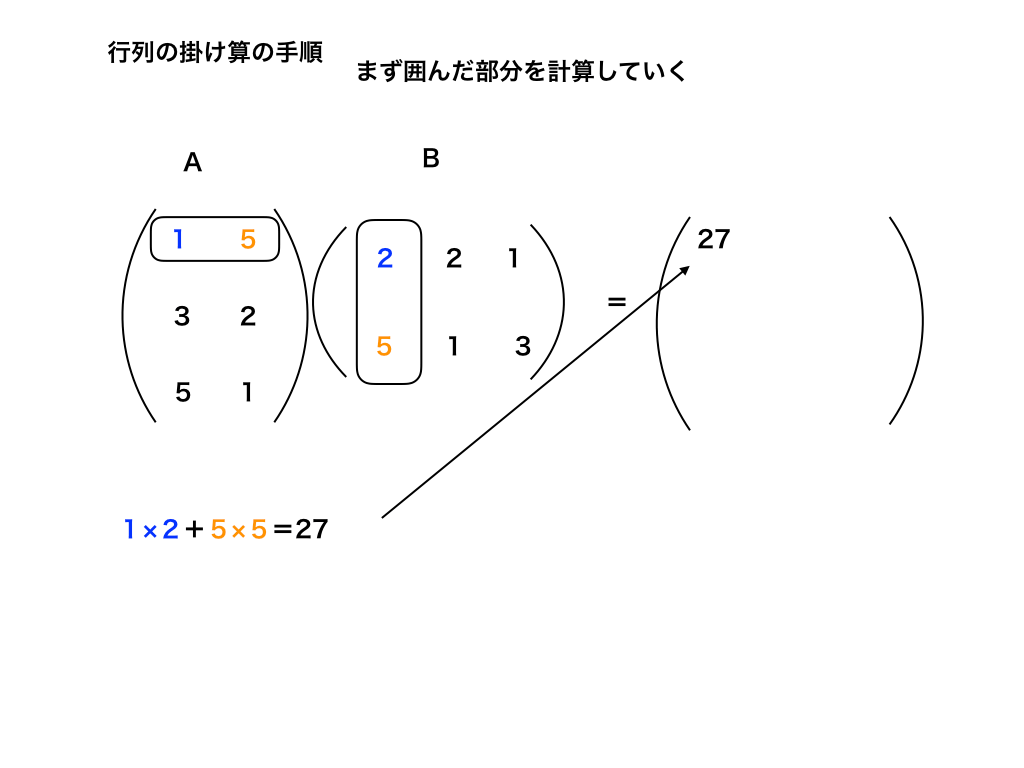
1:1行目と1列目の成分を掛けて足し合わせる
Aの1行1列の成分である「1」と、Bの1行1列の成分である「2」を掛けたものと(図中の青字の部分)、
Aの1行2列の成分「5」と、Bの2行1列の成分「5」をかけた答え(オレンジ色の部分)を足した、「27」をABの1行1列目に書き込みます。
<行列の積の順番1>
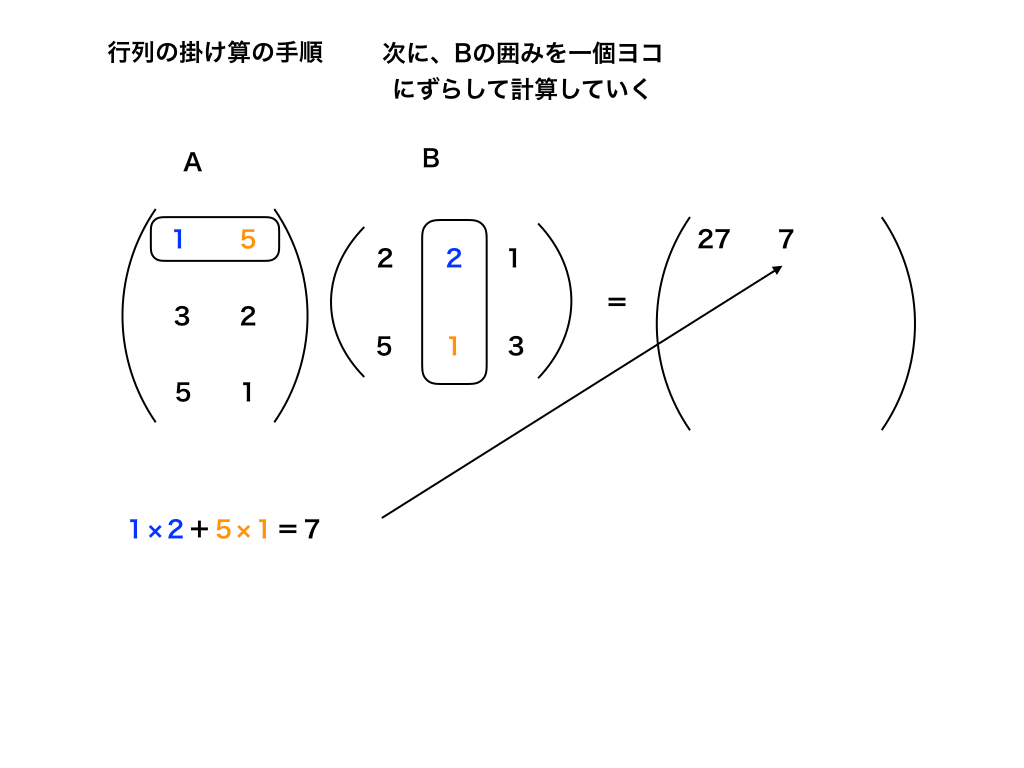
2:1行目と2列目を掛け合わせて行く
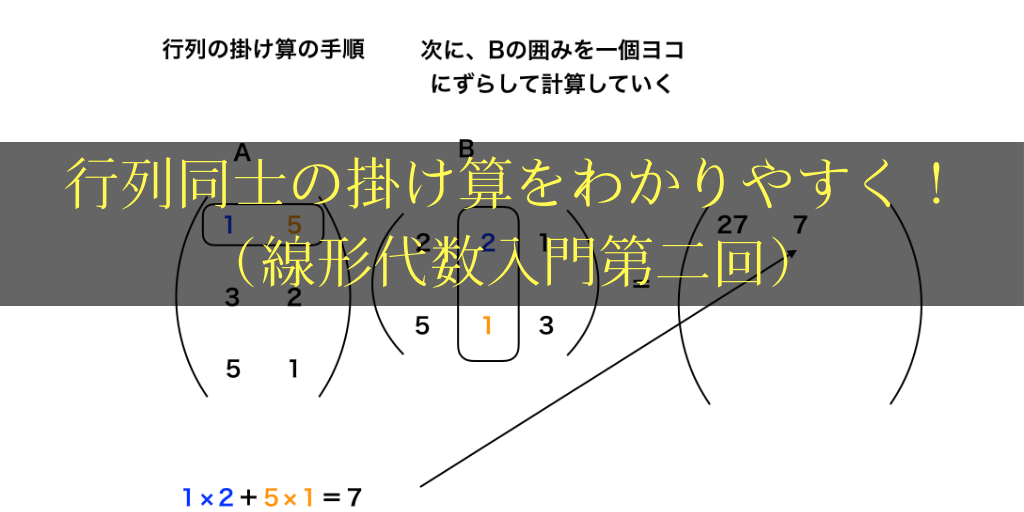
次に、Aの行はそのままBの列を移動して、同じ要領で計算を進めて行きます。
(答えは<図2>の通り「27」のとなりに記入します。)
<行列の積の順番2>
3:1行目と3列目を掛け合わせて行く
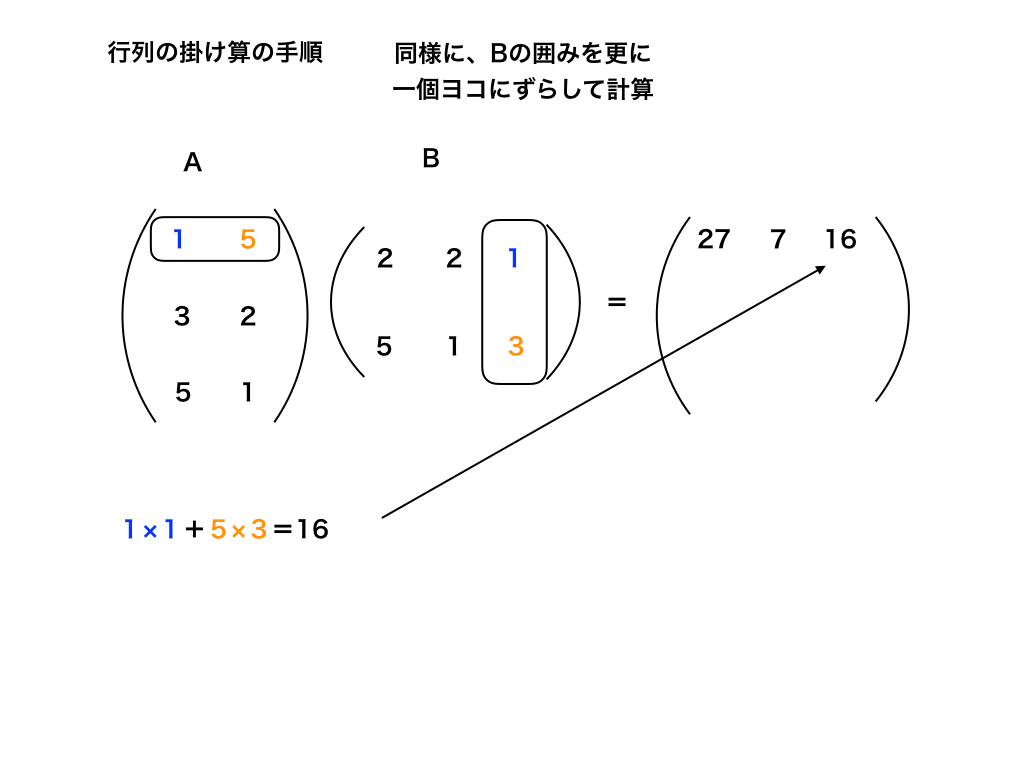
<行列の掛け算の順番3>
4:2行目に移り、1行目と再び掛け合わせて行く
Bの3列目まで計算が終わったら、次はAを2行目に移動し手順1と同様に計算を進めて行きます。
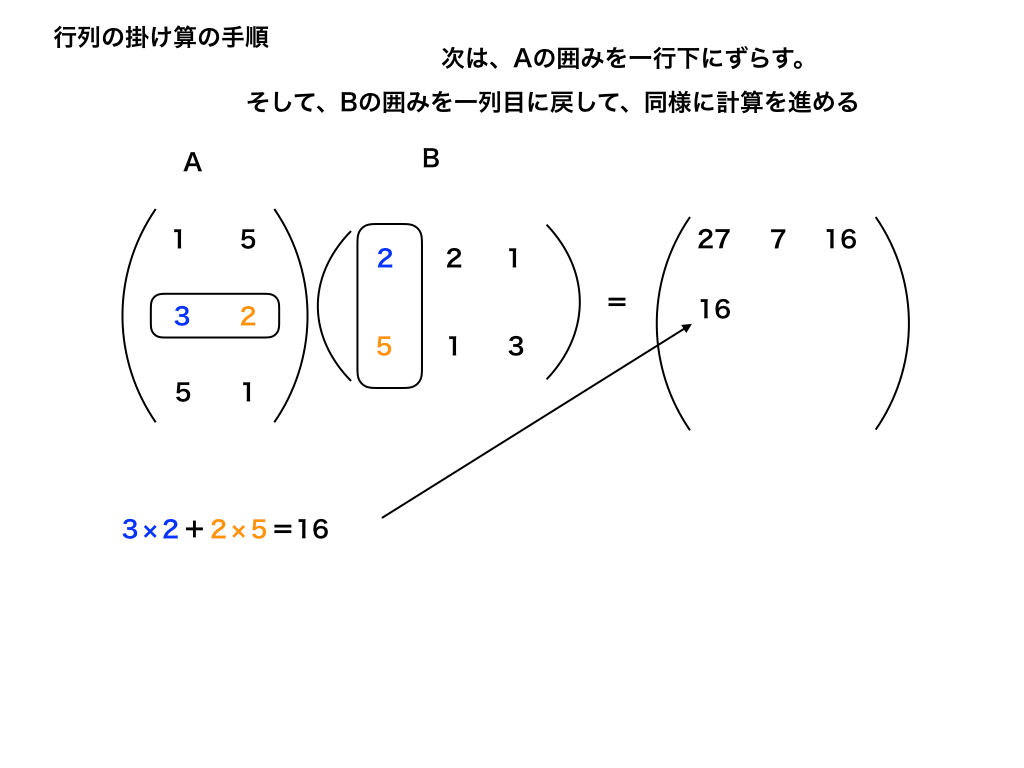
<行列の掛け算の順番4>
5:これを3行目*3列目まで順に行う
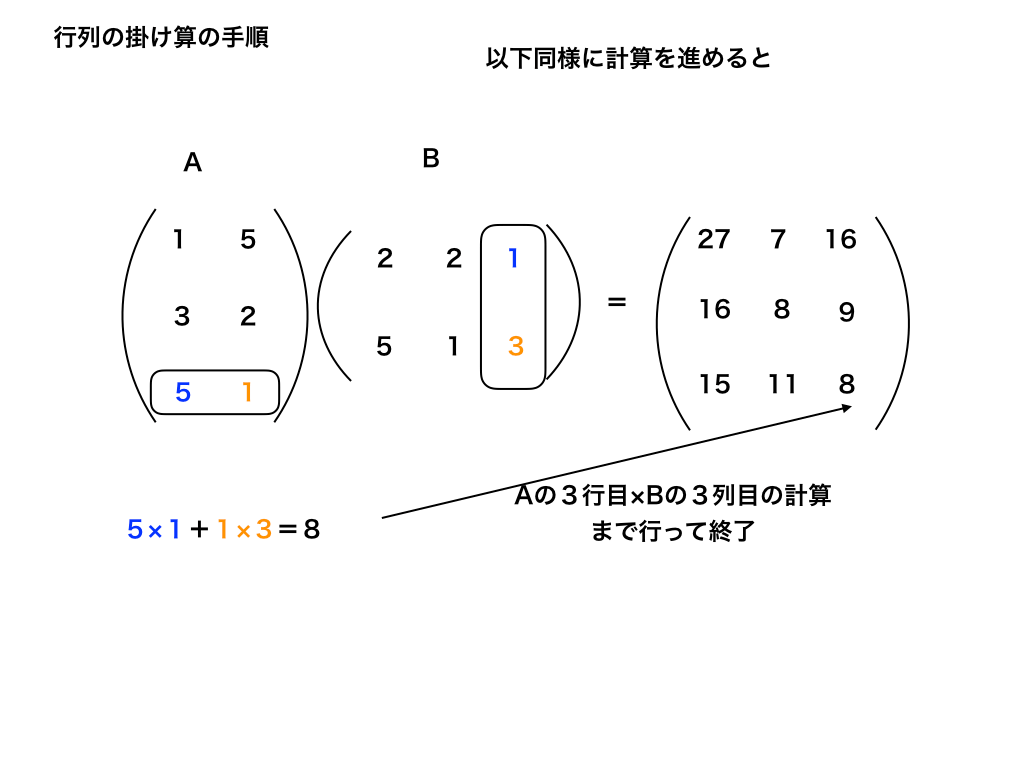
掛け算に慣れるコツ
行列同士での掛け算は、以上の様に非常に複雑でした。行列の掛け算に慣れるコツは、ズバリ「手を動かすコト」です。
今初めて手順を見た人はうんざりしていると思いますが、5回、10回と繰り返しているうちに、
「どことどこを掛け合わせるか」と言ったことは頭を使わなくとも、自然と手が動いている様になります。
以下に定着用例題を用意したので、訓練がてら解いてみてください。
3×3行列の掛け算(定着用例題)
$$(1)A=\begin{pmatrix}
1 & 1 & 1 \\
2 & 2 & 1 \\
3 & 4 & 3
\end{pmatrix}$$
$$B=\begin{pmatrix}
2 & 3 & 1\\
1 & 5 & 1\\
4 & 2 & 1
\end{pmatrix}$$
AB=
答え
$$(1)AB=\begin{pmatrix}
7 & 10 & 3\\
10 & 18 & 5\\
22 & 35 & 10
\end{pmatrix}$$
行列の掛け算の意味と非可換(積の順番)について
ここからは、先ほどの「行列同士での掛け算のルール」でかいた、
「順番が異なると結果も異なる」ことと、行列の積の意味について詳しく説明していきます。
行列の掛け算の意味(変換)へ
ここまでは、『掛け算の仕方』を解説してきましたが、行列をかけるとどのような意味があるのか?についてはまだ触れていませんでした。
その一つとして、行列を掛け合わせる事で座標上の物体が伸び縮みしたり、3次元空間の図形が2次元空間に移ったり、と言う”変換”と言われる事が起きます。
詳しくは:「線形(一次)変換とは何か?イメージで解説」をご覧ください。
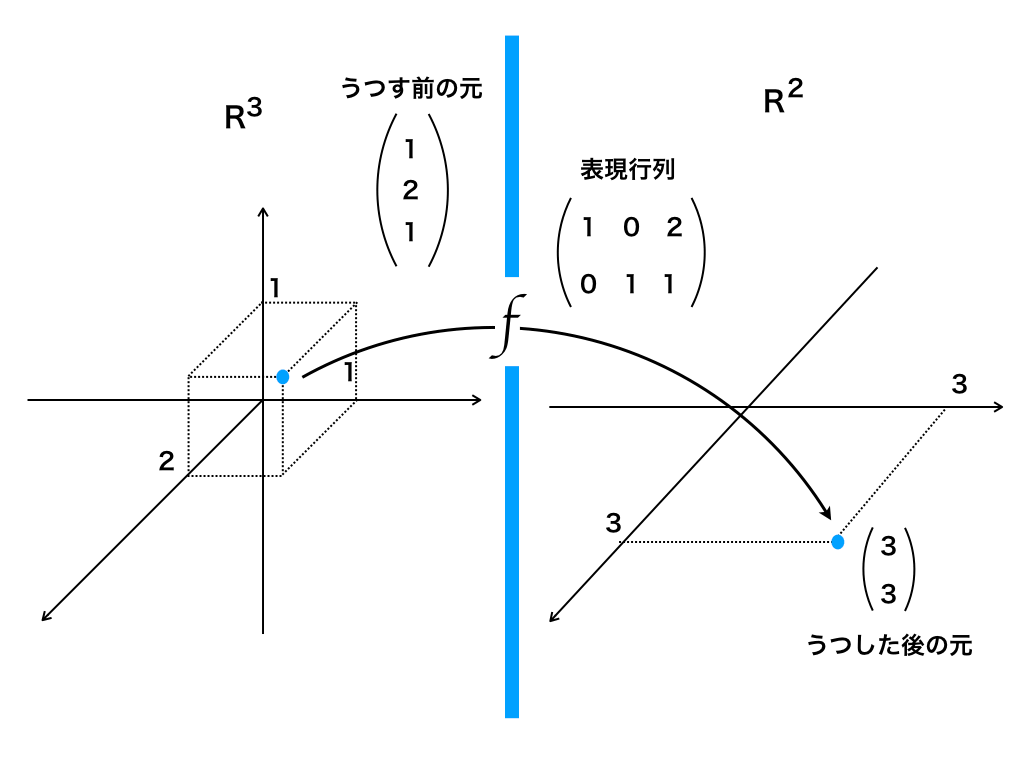
(上の図について詳しくは:「線形写像とIm・Kr」)
正方行列
準備として、「正方行列」というものについて少しだけ触れておきます。
正方行列は、以下の図の様に「列の数と行の数が同じ」=すなわち「正方形のカタチをした行列」のことです。
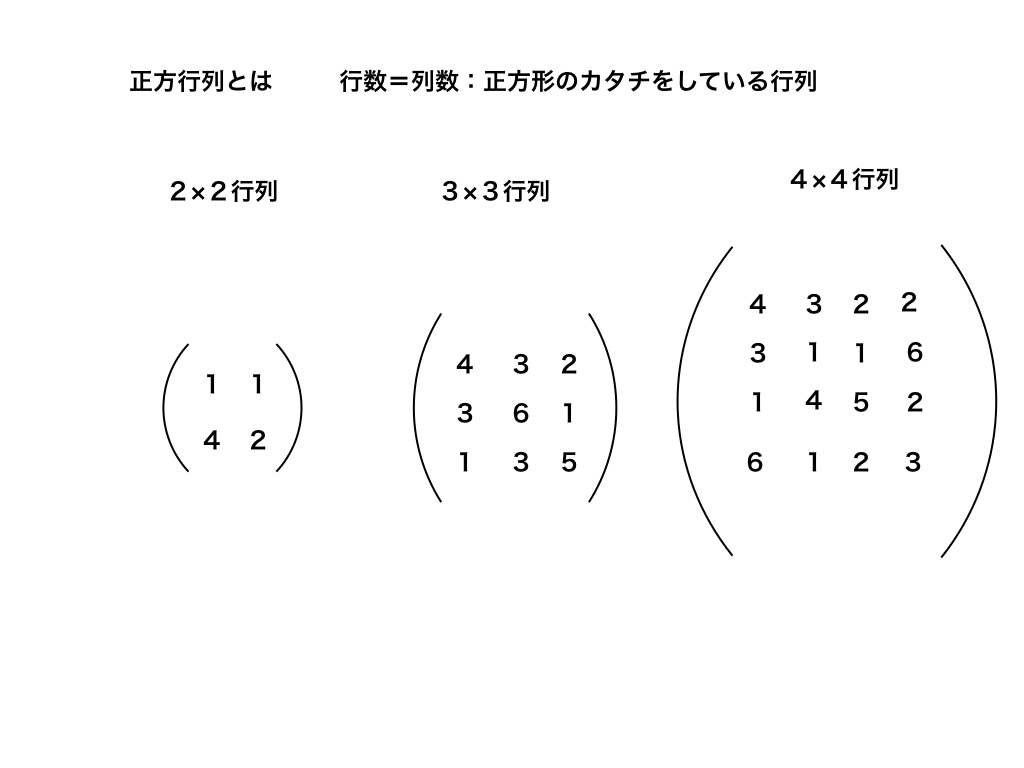
<2行2列から4行4列までの正方行列の例>
非可換を実際に確かめてみる
さて、本当にA*B≠B*Aなのか以下の行列AとBの掛け算で確かめてみましょう。
$$行列A=\begin{pmatrix}
3 & 2\\
1 & 2
\end{pmatrix},行列B=\begin{pmatrix}
4 & 1 \\
2 & 3
\end{pmatrix}とする。$$
$$AB=\begin{pmatrix}
16 & 9\\
8 & 7
\end{pmatrix}$$
$$BA=\begin{pmatrix}
13 & 10\\
9 & 10
\end{pmatrix}$$
この様に、順番が逆になるだけで全く異なる結果になりました。
単位行列と可換
では、どの様な行列同士の掛け算でもAB≠BAとなるのでしょうか?
じつは、どんな行列とかけあわせても答えが同じ(:AB=BA)となる行列が存在し、
その中でも以下の様な成分で表される行列を「単位行列」と呼び“E“で表されます。
$$単位行列E=\begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix}$$
実際に行列Aと単位行列Eの掛け算を順番を入れ替えて計算してみます。
$$行列A=\begin{pmatrix}
3 & 2\\
1 & 2
\end{pmatrix}$$
$$AE=\begin{pmatrix}
3 & 2\\
1 & 2
\end{pmatrix}$$
一方、
$$EA=\begin{pmatrix}
3 & 2\\
1 & 2
\end{pmatrix}$$
となり、確かに
AE=EA
が成り立っています。
単位行列や、可換については次回さらに詳しく見ていきます。
次回:行列の割り算?逆行列の正体へ
さて、今回は相当ややこしく、頭を使ったと思います。
行列の掛け算は今後毎回出てきますが、何度か繰り返しているうちに自然となれてきます。
次回は、四則演算の最後:行列の「割り算」について解説していきます。
単位行列や、正方行列などの用語も頻繁に登場するので、是非今回の内容を復習しておいて下さい。
逆行列の解説記事を作成しました。
>>「行列の割り算?逆行列を徹底解説!」<<
線形代数シリーズ一覧
>>「【随時更新】線形代数シリーズ:0から学べる記事総まとめ【保存版】」を読む<<
線形代数第一回:「行列の意味と計算(足し算・引き算・スカラー倍)」
線形代数第二回:今ここです
線形代数入門第三回:「行列の割り算と逆行列・正則行列(+単位行列の応用)」
今回も最後までご覧いただき本当に有難うございました。
このサイトは皆さんの意見や、記事のリクエスト、SNSでの反応などをもとに日々改善・記事コンテンツの追加更新を行なっています。
・記事リクエストと質問・ご意見はコメント欄までお寄せください。
・多くの学生・受験生の方に利用して頂くためにSNSでシェア(拡散)&当サイト公式Twitterのフォローをして頂くと大変励みになります!
・より良いサイト運営・記事作成の為に是非ご協力お願い致します!
・その他のお問い合わせ/ご依頼等はお問い合わせページよりお願い致します。

