三次関数のグラフと極値の求め方/問題の解き方を解説【数学2:微分】

数学２の微分で最重要の３次関数について徹底解説！

この記事では、

・数学２微分の初学者や、この範囲が苦手な人向けに、

・３次関数の微分とグラフの描き方、極大値・極小値の求め方を解説した記事です。

・最後のまとめ問題を解けるように何度か読み返して貰えれば、苦手→得点源に変えることができるはずです！

是非じっくりご覧ください。

三次関数の微分とグラフ・極値

まず、数学２の微分で扱う基本的な復習をし、微分と傾きの関係を確認したのち、本題の三次関数に入ります。

微分計算の簡単な復習

さて、ここではごく簡単に数学２の微分で利用する計算を復習しておきます。

xⁿを微分するとn・x^(n-1)となります。

微分と傾きの関係

微分と傾きについて理解する為に、y=x²を使って解説します。

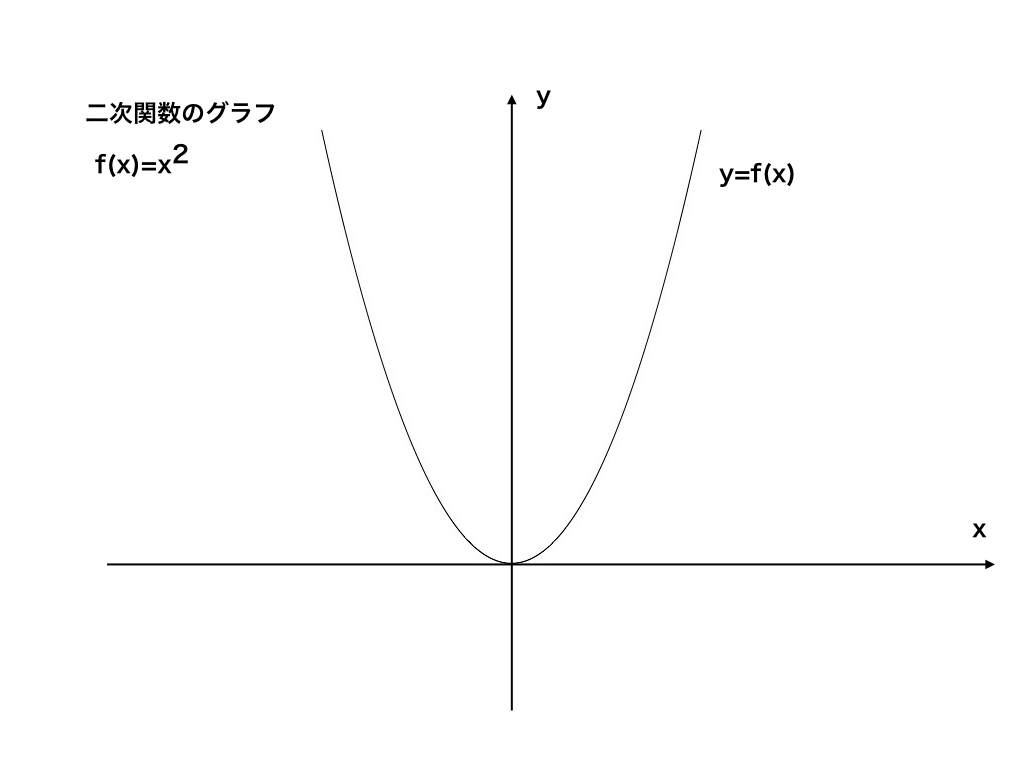
＜f(x)＝x²:y=x²のグラフ＞

この二次関数のグラフはよく見慣れていると思います。

＜関連記事：「二次関数のグラフと解の存在範囲」＞

ここで注目するのは、二次関数のグラフの『傾き』についてです。

x軸マイナス方向からxが０に近づくにつれて、yの値が小さくなっています。

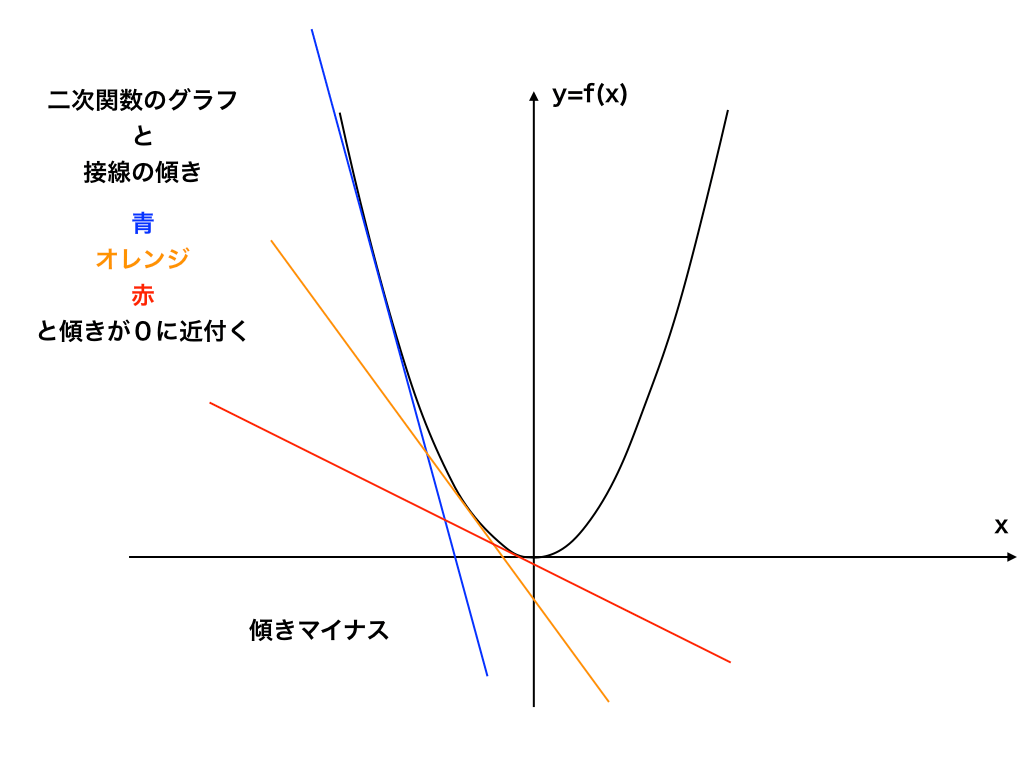
＜二次関数の接線の傾き(x<0)＞

そして、下降している二次関数に接線をいくつも引くと、だんだんと緩やか＝傾きがー（大）からー（小）、そして最終的にx＝０のところで傾きが０になっていることがわかります。

同様に、x＝0からx軸正方向へ向けて接線を調べていくと、だんだんと傾きが大きくなっているのが確認できます。

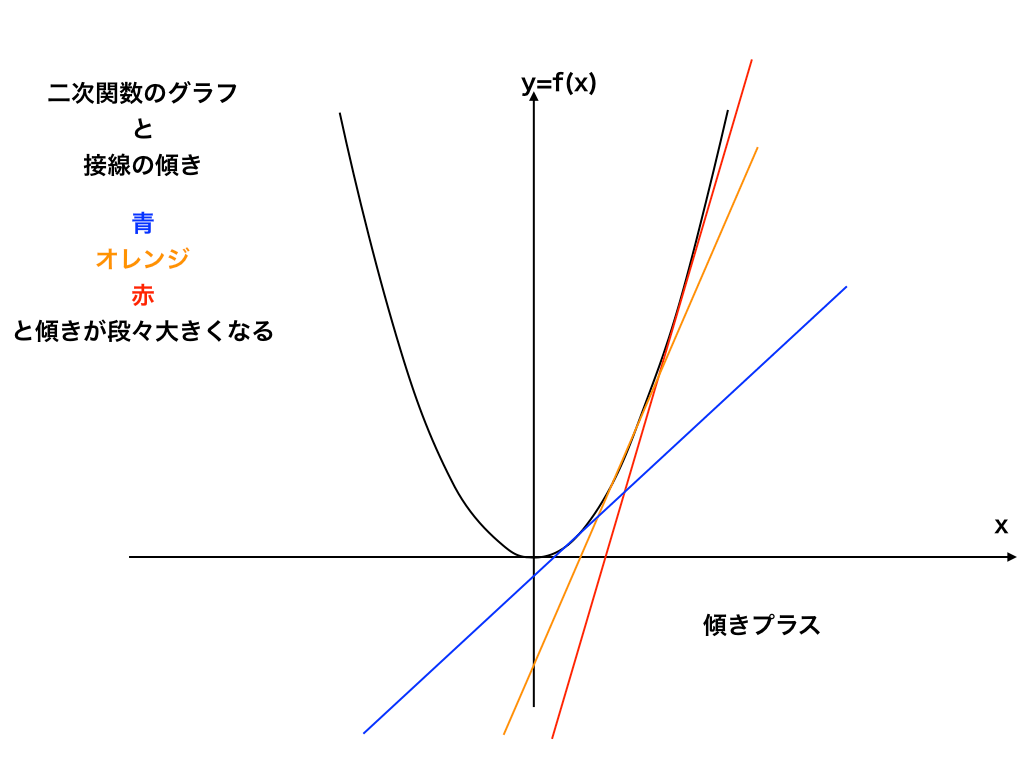
＜二次関数の接線の傾き(x>0)＞

この「傾き」は微分したグラフで表すことができます。ここではf(x)=x²を微分した、

f'(x)=2x のグラフを見てみましょう。

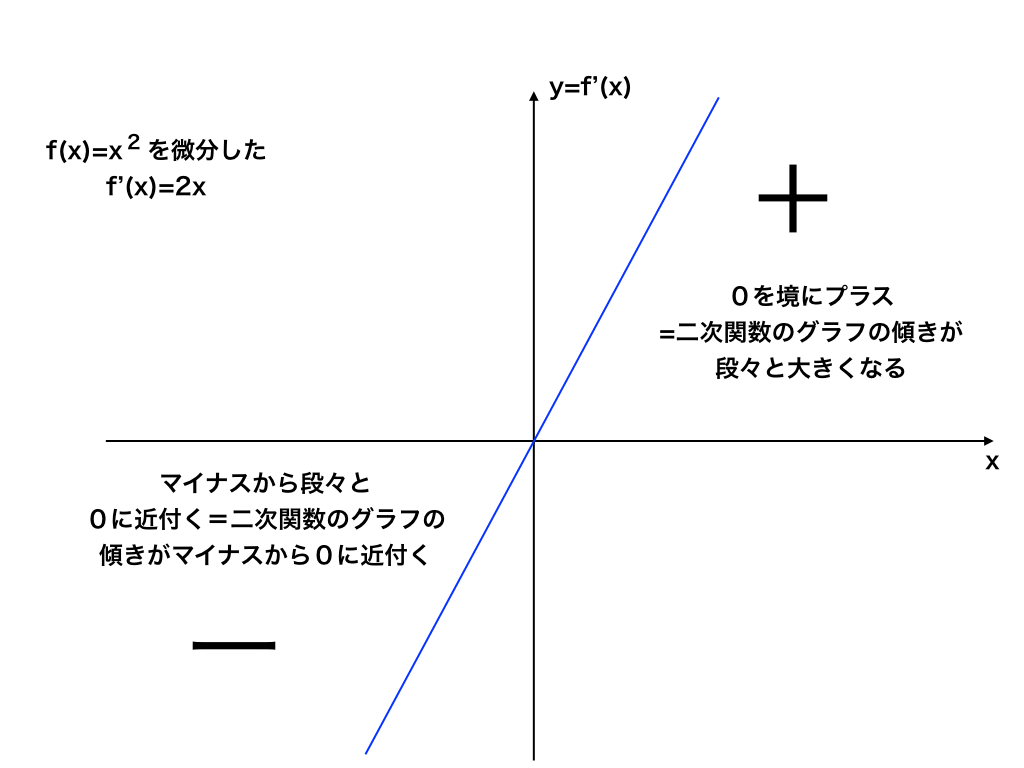
＜f‘(x)＝2xのグラフ＞

上のf'(x)のグラフを見ると、確かに元のf(x)=x²のグラフの接線の傾きが、

微分したf'(x)のグラフで表されることがわかるかと思います。

三次関数を微分し、増減表を作る

上で見たように、n次関数を微分することで（n-1）次の関数になり、さらに（n-1）次関数のグラフの＋ーを調べることによって、元のn次関数がどこで傾きが０になっているのか、などを調べることができるのです。

では、いよいよこの記事のメインである3次関数のグラフの描き方を見ていきましょう。

f(x)＝x³+ 5x²-8x

を例としてみます。微分すると、f'(x)=3x²+10x-8

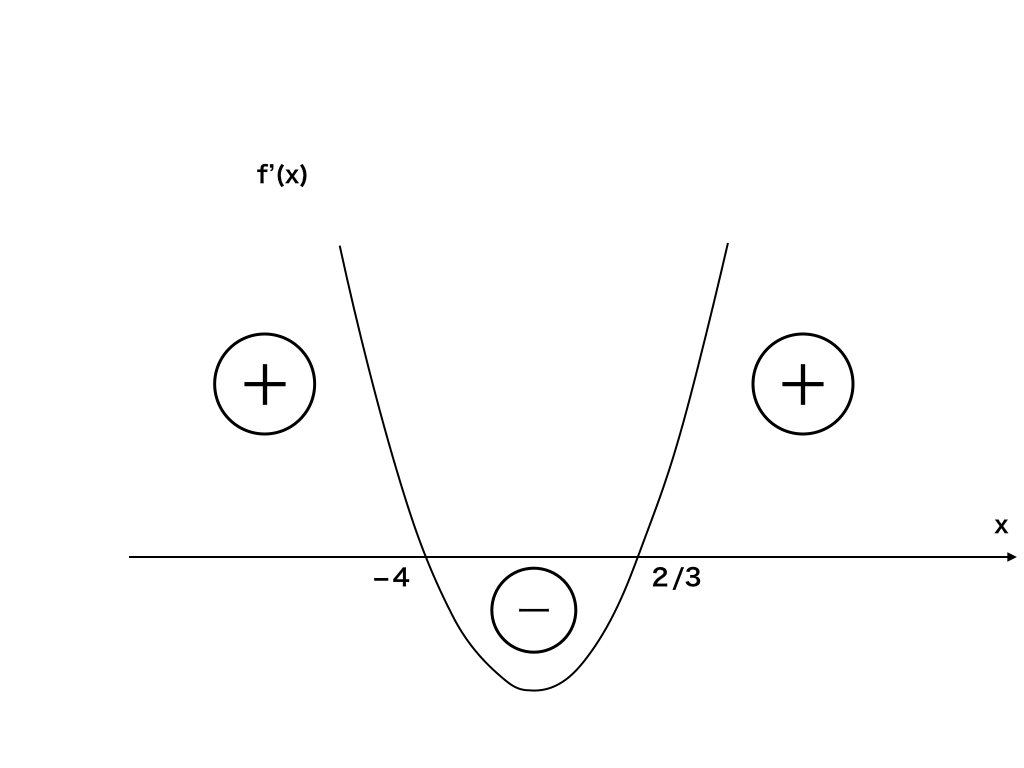
＜三次関数の傾きを微分して調べる＞

この二次関数の解＝f'(x)のグラフのx＝０の部分（x=-4と2/3）を境に、

値が＋からー、ーから＋へと変化しています。

微分してできた、二次関数は三次関数の『傾き』だったので、

この符号が変化するところ（x＝−４）を境にして元の三次関数のグラフが上昇から下降、

（x＝2/3）を境にして下降から上昇へと変化することがわかります。

この点のことをそれぞれ「極大値」、「極小値」と言います。

これらを使って次の項で解説する三次関数のグラフを描いていきます。

増減表と極値

f(x)とf’(x)が0になる点が分かっても、慣れないうちはすぐにグラフを描くことは難しいです(*1)。

そこで、これらの情報をまとめてグラフを描く時の参考にするのが“増減表”です。

増減表の作り方は、

１：下図の左端に書いてあるように、x、f'(x)、f(x)の箱を作り、

２：今度はxの箱の横に、f'(x)=0となる「２つの境目（f'(x)とx軸との交点のx座標）」と、その左側・右側・２交点の間の５箇所に区切ります。

３：次に、f'(x)のグラフ＜上の図参照＞を元にして、f'(x)の箱の横の、＋、ー、０となる場所を埋めていきます。

４：最後に、一番左下のf(x)の行に注目して、f'(x)>0のところは↗︎（上昇している）、f'(x)＜0のところは↘︎（下降している）そして、f'(x)=0のところには、xの値をf(x)=x³+5x²-8xに代入して書き込みます。

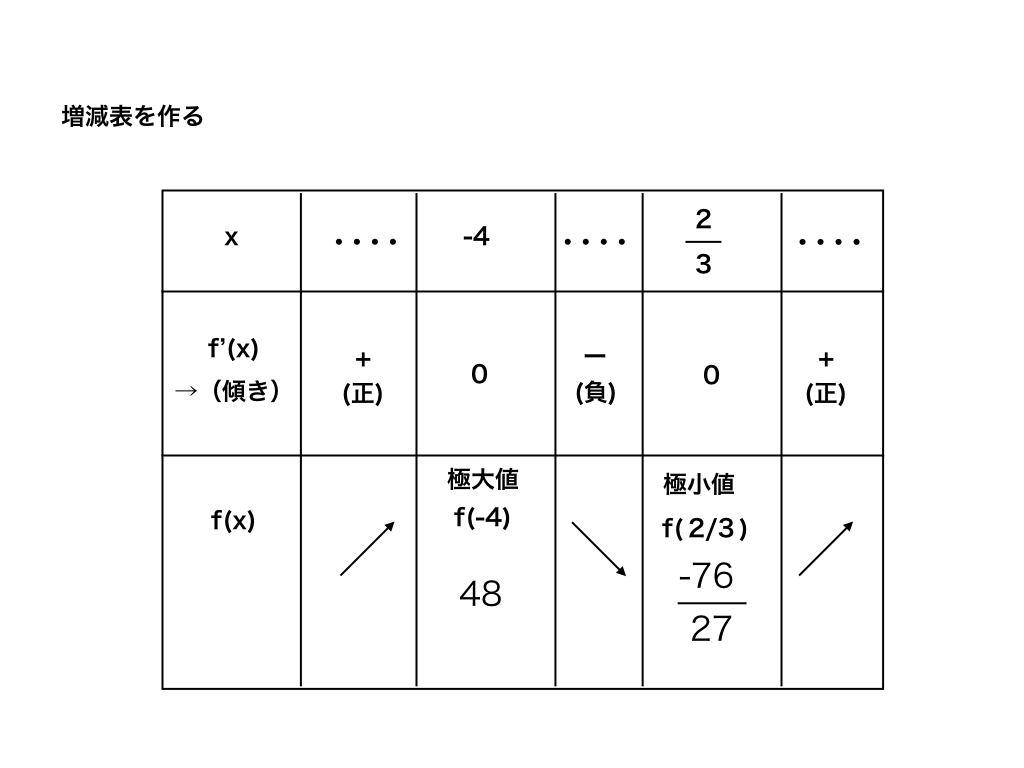
＜三次関数の増減表＞

以上の１〜４の作業を行うことで、上のような”増減表”を作成することができます。初めは大変に思えるかもしれませんが、慣れると簡単に作成できるので、いろいろな類題に当たって素早く作れるように練習してみましょう。

 

(*1:増減表について:ここでは、入門レベルの記事なので増減表を積極的に利用します。ただしレベルが上がってきたり、数学3を学ぶ人は(最終的には)増減表を利用しなくともグラフのカタチがわかる様になってきます。→「増減表をはじめから作らず、グラフを描く方法（数学３）」)

三次関数のグラフ

これまでの情報を整理した、『増減表』を使って例題の3次関数:(f(x)＝x³+5x²-8x)のグラフを描いてみましょう。

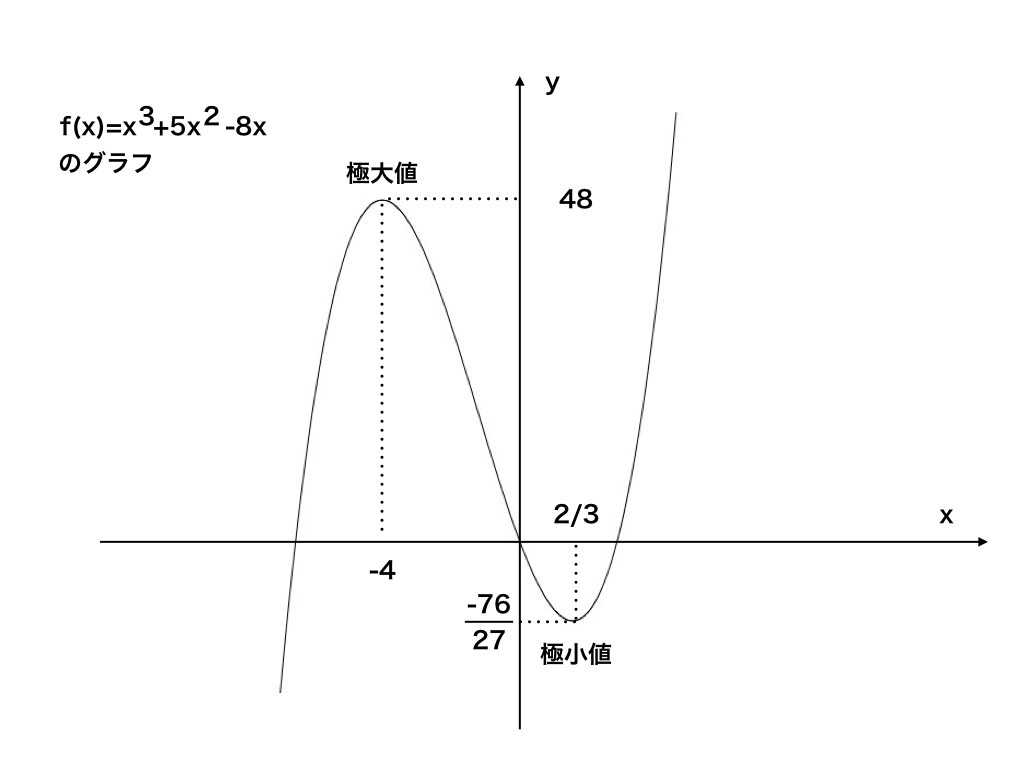
＜例題の三次関数のグラフ＞

【数２】三次関数のまとめ問題【微分】

ここでは、数２の微分でよく問われる三次関数の問題(特に極値についての問い)を使って、

この記事の内容を確認していきます。

極値の存在条件に関する問題【応用１】

極大値・極小値を合わせて極値と呼びましたが、どんな三次関数にも極値があるという訳ではありません。

【応用問題1】:f(x)＝x³+ax²+x+2 の関数が極値を持たないために満たすべきaの値を求めよ。

極値の情報から、3次関数を決める問題【応用２】

あらかじめ極大・極小値などの情報が与えられて、関数を求める問題も頻出です。

【応用問題2】:f(x)＝x³+kx²+lx+m の関数が、x=1で極大値9を取り、

x=5で極小値aを取るとき、この三次関数と極小値aの値を求めよ。

解答解説

 

問１：極値の存在条件と判別式D

まず、極値が存在する条件を考えると、問題の三次関数を微分した二次関数の符号が＋からー、ーから＋へと変化する点（＝二次関数とx軸との交点）が存在することでした。

逆に極値が存在しない、ということはf'(x)=(二次関数)がx軸と交わらず浮いているような状態＜図１-1＞か、x軸と接するが符号は変化しない（＋→０→＋）＜図1-2＞のどちらかである必要があります。

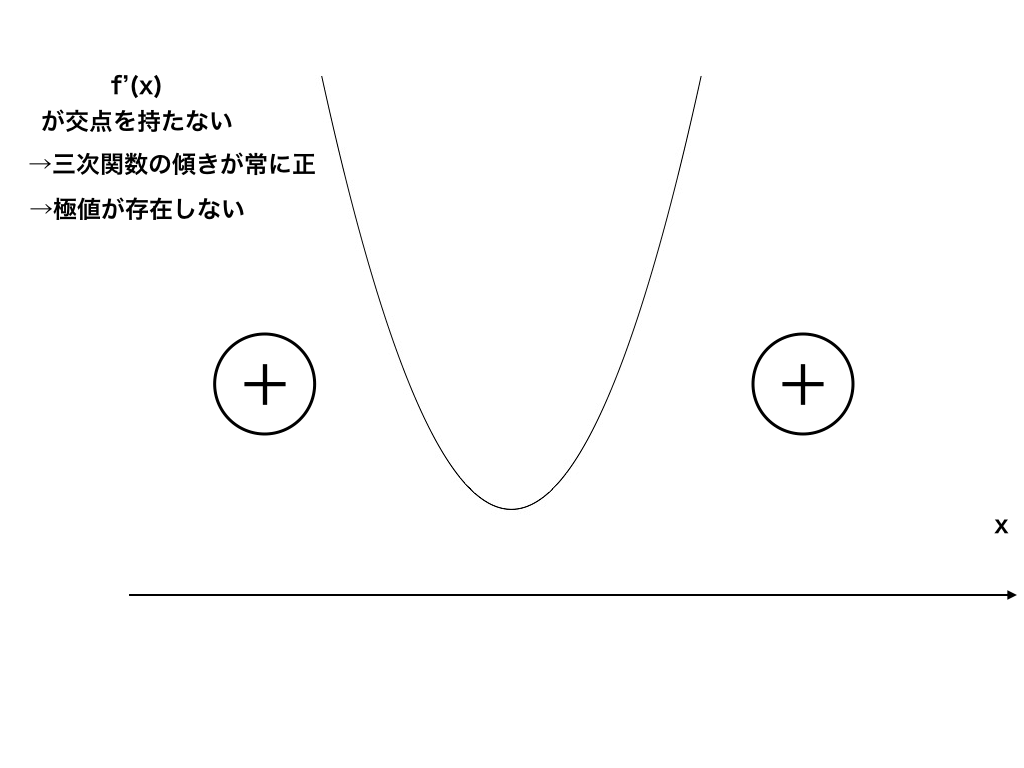
＜図1-1:f‘(x)の交点が０→判別式D＜0＞

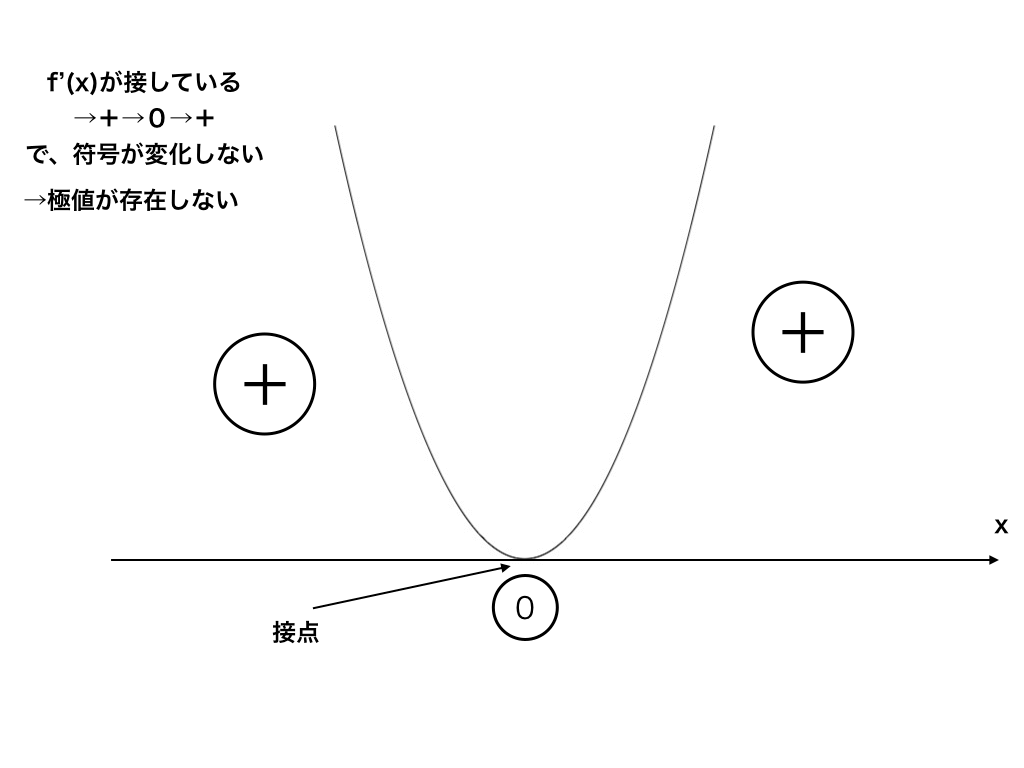
＜図1-2:f‘(x)の交点が１つ→判別式D=0＞

要するに、f'(x)のグラフが解を持たないか、１つ（重解）を持っているかのどちらかであればf(x)のグラフは極値を持たないと言えます。

二次関数の解の個数を調べるには、”判別式D”を利用します。D≦０がこの問題の条件を満たすので、

判別式D＝4a²-12≦0 ⇔a²-3≦0 より、題意をみたすaの範囲は、「-√3≦a≦√３」・・・（答）

問２：極値の情報から三次関数を定める

問２では、極大値とその時のx、極小値をとる時のxの値の３つの情報が与えられています。

f(x)＝x³+kx²+lx+m のグラフが、“x=1で極大値9”を取り、“x=5で極小値aを取る”ことから、極値をとるxの値は、1と5であることがわかります。

先ほどから解説しているように、極値をとる＝傾き0⇔f’(x)＝0なので、f‘(x)のxに1と5を代入すると、f‘(1)＝0、かつ、f‘(5)＝0になります。

さらに、x=1でf(x)＝9をとることより、f(1)＝9の式も立てることができます。

以上の3式と、f’(x)＝3x²+2kx+l より

f‘(1)＝3+2k+l=0

f’(5)＝75+10k+l=0

よって、k=-9、l=15

f(x)＝x³-9x²+15x+m

f(1)=９（極大値）より、1-9+15+m=9

従って(k,l,m)＝(-9,15,2)・・・（答）

これをf(x)＝x³+kx²+lx+mに代入し、x＝５の時極小値aをとるから、

f(5)＝ 125-225+75+2=-23、ゆえに極小値a=−２３・・・(答)

まとめと関連記事一覧

・今回は少しボリュームが多かったかもしれませんが、この一記事で数学２の微分に関してはかなりの部分をカバーできます。

・次回は、数２微積の発展問題について解説します（製作中）

・理系の人で、数学３の微分・積分を先取りしたり、復習したい人は→「数学３の微分・積分法の基礎から応用までのまとめ」に進んでみてください！

 

最後までご覧いただきまして、有難うございました。

「スマホで学ぶサイト、スマナビング！」は読者の方の、

反応などをもとに改善、記事の追加、更新を行なっています。

リクエストやご質問がございましたらコメント欄にお寄せください。

また、snsでいいね！やシェア、B！、Twitterのフォローをしていただけると助かります。