電場/電気力線とガウスの法則
今回は、「点電荷が作る電位と電場」の記事の続編です。
本格的には大学で(マクスウェル方程式+ベクトル解析)学びますが、知っておくと有利な事があるので、高校数学/物理の範囲内で「ガウスの法則」について解説します。
目次(タップした所へ飛びます)
電場を電気力線で見える化する
・はじめに
・点電荷が作る電場Eの導出の紹介
・電気力線の導入
・点電荷から出る電気力線
・ガウスの法則導入
・点電荷を囲んで電気力線の総本数を算出する
・これをどう使うか?平行板コンデンサーへの応用
はじめに
今回は、点電荷から出る電気力線と電場の関係、更にガウスの法則を解き明かしていく事で、式の深い理解を得る事を目標にします。
さらに、点電荷の代わりに平行版から出る電気力線を考えることで、コンデンサーの記事へスムーズに進むことができるように解説して行きます。
点電荷が作る電場Eの導出の紹介
点電荷とは、正、又は負の電荷を持つ極々小さな物質と考えて下さい。
+ Q(C)の電荷を帯びている点電荷は周りに電場Eと電位Vを生み出します。
この詳細な説明は以下の記事で行っていますので、先に必ずご覧下さい。m(__)m
......
......
さて、少し難しかったと思いますが、大体の流れとV= E= の式が頭に残れば十分です。
ちなみに、知っておくべき事として、真空中でのクーロン定数\(k_{0}\)は真空の誘電率\(ε_{0}\)を用いて
k0=1/(4πε0)と表せます。
$$k_{0}=\frac {1}{4\pi \varepsilon _{0}}$$
では、先ほどの記事で得た点電荷が作る電場Eの知識をもとに、「電気力線」に入って行きます。
電気力線
電気力線とは、電場の様子を「見える」様に考え出されたもので、線の本数(密度)と向きで電場の強さと向きがわかります。
具体的には、電場がE(N/C)の場所では、電場に垂直な\(1m^{2}\)の面積当たり\(E(本)\)の電気力線が存在するという風に定義されています。
点電荷から出る電気力線
先ほども取り上げましたが、点電荷がr(m)の場所に作る電場Eは$$E=\frac {k_{0}Q}{r^{2}}$$
では点電荷が作る電気力線の総本数を数えたい時、どうすれば良いでしょうか?
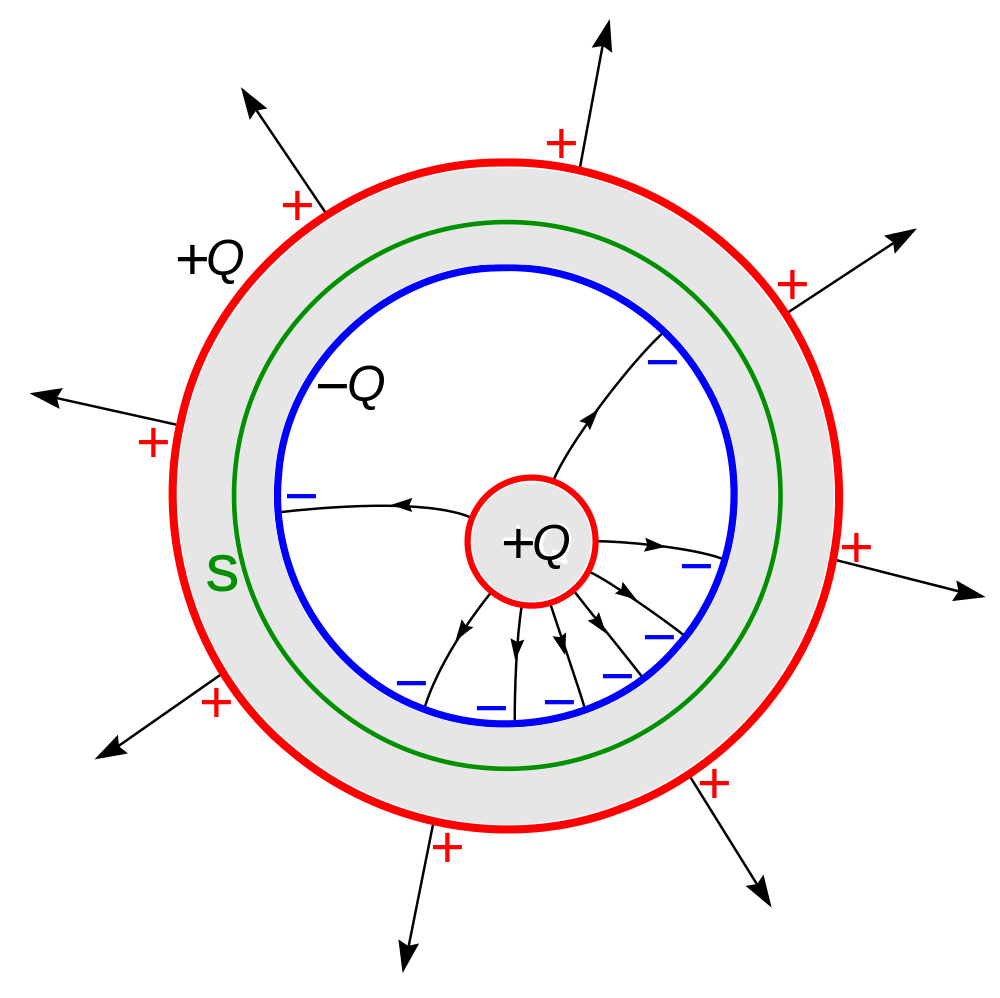
ここで「点電荷を半径rの球で囲む」という事を考えます。
ガウスの法則と電気力線の本数
前の項で考えた『電気力線の総本数を求める』→球体で囲む?という言葉と考え方の意味を詳しく紹介していきます。
「点電荷を囲む」という発想の元となるガウスの法則
大学学部レベルの範囲である事と、面積分(ベクトル解析)が必要なので、詳しくは割愛しますが、
この法則を利用して、下の計算では閉曲面を球とし、電荷はQでただ一つなので、Σq=Qとして計算しています。
(ちなみにこのガウスの法則が素晴らしいのは、閉曲面;すなわち閉じた曲面を持つどんな図形にも応用出来る所です)
今回は球で囲みますが、ジャガイモのようなカプセルでも内部のQ電荷からは同じ本数の電気力線が出てきます。
球で点電荷を囲み電気力線の総本数を計算

総本数をNall(本)、囲む球の表面積をS(m^2)とすれば、\(N_{all}=E・S\) で計算できます。
E=(k0・Q)/r ^2 ⇔E=Q/4πε0r ^2(本)
$$E=\frac {k_{0}Q}{r^{2}}=\frac {Q}{4\pi r^{2}\varepsilon _{0}}$$
\(S=4\pi r^{2}\)
\(\begin{aligned}E\cdot S=\frac {Q}{4\pi r^{2}\varepsilon _{0}}\times 4\pi r^{2}\\
=\frac {Q}{\varepsilon _{0}}\end{aligned}\)
∴ N all={Q/(4πε0r ^2)}・(4πr ^2)
∴ N all=Q/ε0(本)
$$N_{all}=ES=\frac {Q}{\varepsilon _{0}}$$
綺麗に\(4\pi r^{2}\)が消えました!
この様に計算する事で、点電荷が作る電場Eは総本数Q/ε0の電気力線を出していることが分かりました。
平行板コンデンサー(一様な電場)へ
では、そもそもこの電気力線を考える事にどの様な意味があるのでしょうか?
「電場」を見える化するだけでなく、コンデンサーの諸公式や極板間引力などを理解しやすくなります。
通常のコンデンサーの解説記事が完成次第、「電気力線とコンデンサー」の記事を追加予定です。
コンデンサー関連の記事
「コンデンサーの"仕組みと公式"の意味がわかる!高校物理電磁気」
「コンデンサーの"電気容量"を徹底的に!並列・直列接続と誘電体による変化」
(2018/09/23:電荷に関する関連記事:点電荷についてマスターしたい人は
>>【座標上の2つの点電荷が作る電場と電位・点電荷の力学との融合問題】<<をご覧ください)
質問、記事リクエスト、誤植はコメント欄、その他のお問い合わせとご依頼はお問い合わせページまでお願い致します。

