
点電荷と力学の融合
この記事では、「点電荷の作る電位と電場を図と計算で理解する」の続編として、座標上の2つの点電荷が作る「電位・電場」の計算問題と、有名問題である『点電荷の運動を計算』する力学分野との融合問題を通して、前回の内容の完全な理解を目指します。
<オススメ記事>:「電磁気(高校物理)総まとめページ」
目次(タップした所へ飛びます)
点電荷と座標の問題は「電位:スカラー」.「電場:ベクトル」を強く意識せよ!
「点電荷が作る電位と電場」の問題で任意の(X,Y)座標の電位や電場を求めさせたり、
任意の点の電位・電場が0になる点電荷のおき方が問われる事が非常に多いです。
ここで注意が必要な事として、電位はあくまでスカラー量(大きさの1情報だけを持つ)で、
電場はベクトル量(大きさと向きの2つの情報を持つ)であることをしっかり確認しておきましょう。
もしベクトル量とスカラー量の違いが曖昧だったり、ベクトルの足し算・引き算が苦手なら
→「ベクトルとは?0から始める徹底解説記事9選」この記事が参考になります。
(最低限冒頭部と、ベクトルとは何か)の記事を読むと今後も役に立つはずです。
では、少し点電荷が作る電場と電位について復習しておきましょう。
クーロンの法則と点電荷が作る電場Vと電位E
クーロンの法則とは、Q1(C)の電荷とQ2(C)を持つ点電荷の間に働く静電気力(クーロン力)Fを求める式で、
クーロン力を求める公式は、
・クーロン定数k
・2つの点電荷間距離をrとして、
$$F=k× \frac {| Q_{1}| × | Q_{2}| }{r^{2}}$$
で求まります。
これを応用する事で点電荷が周囲に与える“電気的な傾き=電場E”、“電気的な高さ=電位V”を計算する事が出来ました。
クーロンの法則から点電荷による電位V・電場Eの求め方は、
右の記事(前回の記事)で詳しく説明しているので→「点電荷の作る電位と電場を図と計算で導く」、式のみ記しておきます。
$$V=k\frac {Q_{1}}{r}\cdots(1)$$
$$E=k\frac {Q_{1}}{r^{2}}\cdots(2)$$
ここから本題です。
2つの点電荷が作る任意の点での電位
下の問1・問2のような問題を見かけた事が有るのではないでしょうか?

<図一:2つの点電荷が作る電位>
問1:<図1>中の点A(-1、0)に+Q(C)点B(1、0)に +2Q(C)の点電荷を置いた時の点P(0,1)での電位を求めよ。
電位はスカラーなので、(1)式を単純に足し合わせるだけで求める事が出来ます。
すなわち、AP間の距離とBP間の距離は共に√2。先ほどの(1)式に代入すると、点Aの電荷による
$$電位は、k\frac{Q}{\sqrt {2}}$$
同様に点Bの電荷による電位は、
$$k\frac{2Q}{\sqrt {2}}$$
$$2つを足して、k\frac{3Q}{\sqrt {2}}$$
2つの点電荷が作る任意の座標上での"電場"【要注意】
さて、今度は"電場"を見ていきます。
繰り返しになりますが、電場はベクトルで表されるので、
電位の場合と同じように「大きさ」だけの足し算/引き算をする事は出来ません!
足し算引き算もベクトルで行う必要があります。
<参考:「ベクトルの足し算/引き算:物理(基礎)で困らないための三角比とベクトル講座」>
具体的に、次の様な場合を考えてみます。
問2:点A(-1、0)に+Q(C)、点B(1、0)に +1Q(C)の点電荷をそれぞれ置いた時、点P(0,1)での電場の大きさと向きを答えよ。
まずは(2)式で点Aと点Bが点Pに与える電場を計算し、次にベクトルであることを考慮して計算します。
電場Eの【大きさ】は、点A・点B共に同じで、
$$(2)式よりk\frac{Q}{\sqrt {2}^{2}}$$
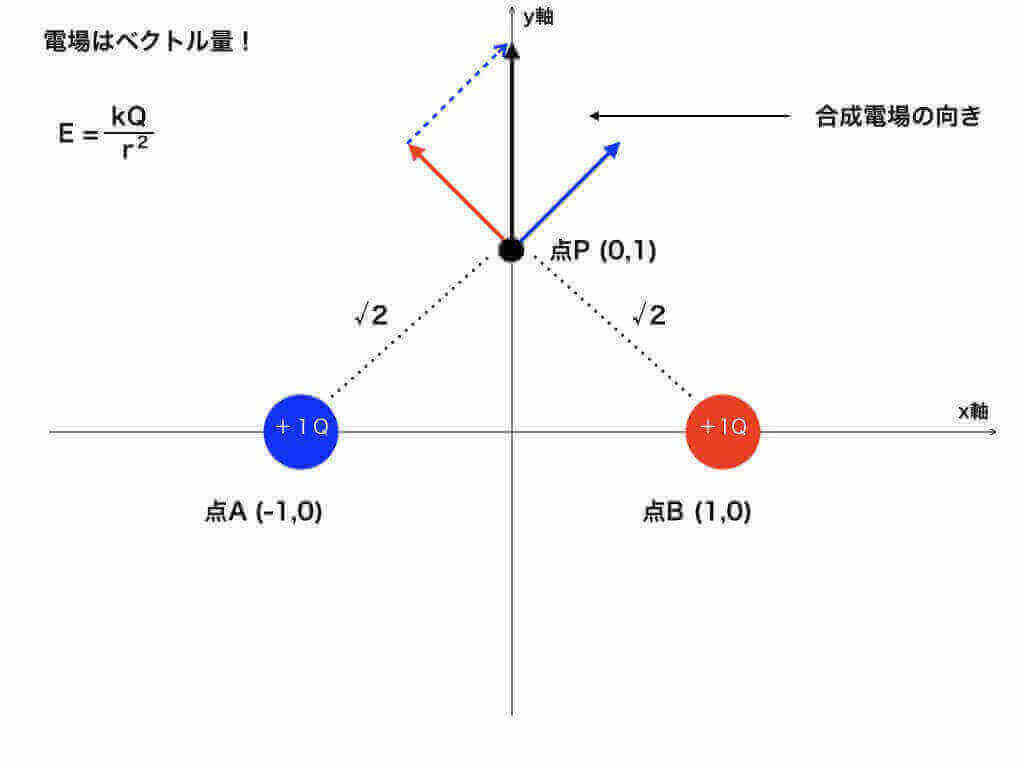
<図2:点電荷が作る合成電場>
あとは、<図2>の様にベクトルの足し算をすると、点Pでの電場は、向きはy軸正方向,
$$大きさ\frac{\sqrt{2}kQ}{2} (N/C)になります。$$
点電荷の運動:力学との融合問題
先に問題をのせます。
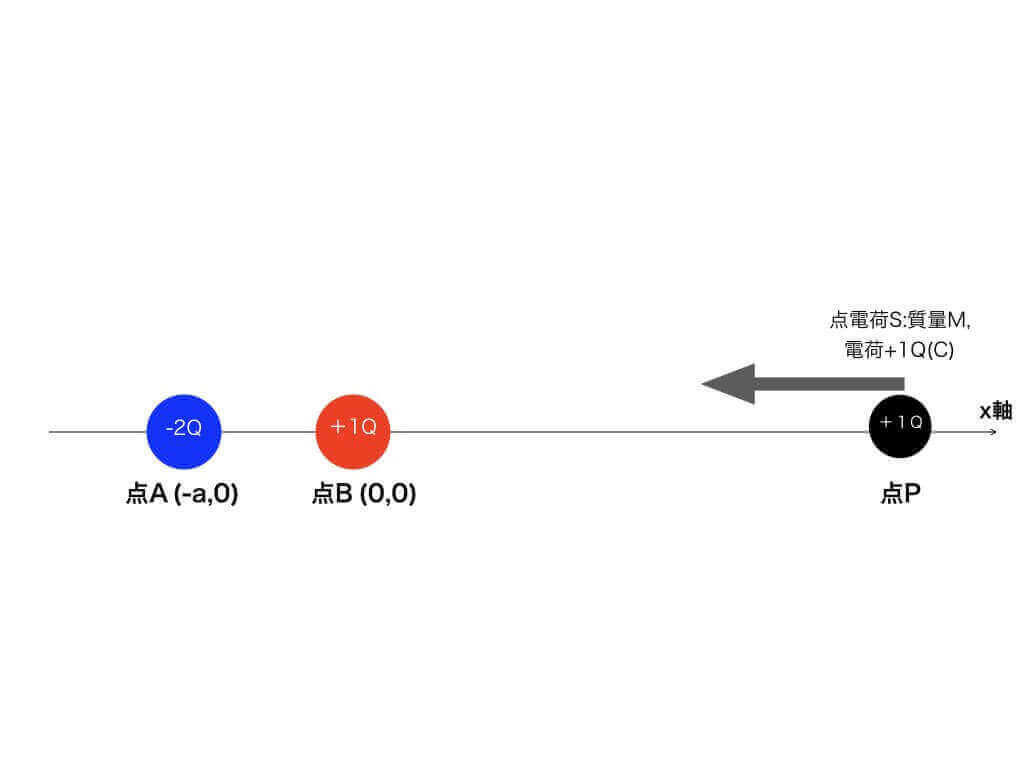
<図3:点電荷と力学の融合問題>
今、<図3>の様にx軸上の点A(-a,0)に-2Q(C)の点電荷を固定し(a >0)、点B(0、0)には+1Q(C)の点電荷を固定する。
ここで、図のx軸上の点Pに +1Q(C)で質量Mの点電荷Sを置くと、x軸負方向へSが動き出した。
ただし重力は考慮せず、電位の基準点を無限遠点にとるとき、以下の問いに答えよ。
問1:Sは点Bに向けて動き出したが、やがてある点Tで停止した。この点Tの座標を求めよ。
問2:Sが点Tに到達するまでに点Uで速さが最大になった。この点Uの座標を求めよ
問3:点UでのSの速さを求めよ。 <有名問題>
数値・文字はそれぞれ少し違うものの、問われる内容と解法はほぼ同じ、かつ頻出の問題です。
点電荷と力学の融合問題の解き方
この問題文を読むと、点電荷Sは点Aに固定された、マイナスの電荷による電場(EAとする)によって引き寄せられていますが、点Bが正電荷であることから点Bを越してx軸負方向へ進めない事がわかります。
解答1:では、どのくらい点Bに正電荷Sは近づく事ができるのでしょうか?
点電荷Sは正の電気を帯びているので、電位が0の点があればそこで運動を停止します。
(その位置以上に点Bへ近付こうとしても、正電荷同士の斥力によって運動が妨げられます。)
つまり問1で問われている点Tは、点Bの正電荷が作る電位VBと、点Aの負電荷によるVAを足し合わせた”電位が0になる位置”だと言うことがわかります。
\(V_{T}=0\)となる座標(x,0)を計算すると、点電荷による電位の式(1)より、
$$V_{B}+V_{A}=k(\frac{-2Q}{x+a})+k(\frac{+Q}{x})$$
$$⇔ kQ\times (\frac{-2x+(x+a)}{(x+a)(x)})$$
$$\frac {-kQ(x-a)}{(x+a)x}$$
この式=0を満たすxの値は、aです。従って、運動が停止する座標は(a、0)・・・(答)
解説2・3 ここでは点Tまでで速さが最大になる点を問われています。
E(電場は電位を微分した“電気的な傾き”)なので、
E=0ならばそれ以上は加速しません。つまりその点がUであり点電荷Sが最速となる場所です。
\(E_{A}+E_{B}=\)
$$-k(\frac{2Q}{(x-(-a))^{2}})+k(\frac{Q}{x^{2}})$$
$$⇔ \frac{kQ(-2\times x^{2}+(x+a)^{2})}{x^{2}\times (x+a)^{2}}$$
$$\frac {kQ(2ax+a^{2}-x^{2})}{x^{2}(x+a)^{2}}$$
この、(式)=0を満たすxの2つ値は2次方程式の解の公式より
\(a\pm a\sqrt{2}\)ですが、\(a-a\sqrt{2}\)の方は
点Aと点Bの間にあるので不適です。
従って点Uの座標は\((a(1+\sqrt{2}),0)\)
最後に、点UでのSの速さは:W=QV(電気的な位置エネルギー)が運動エネルギーに変換された物なので、
エネルギー保存則より、\(QV_{U}=\frac {Mv_{u}^{2}}{2}\)
$${v_{u}}^{2}=\frac {2QV_{U}}{M}$$
$$これを解いて、v_{u}=\sqrt {\frac {2QV_{U}}{m}}$$
ここで、電位の式
$$V=\frac {kQ_{1}}{r}\cdots (1)より$$
$$V_{U}=\frac {kQ}{a+a\sqrt{2}}を上の式に代入して$$
$$v_{u}=Q\sqrt {\frac {2k}{(a+a\sqrt{2})M}}$$
以上より、\(座標U(a(1+\sqrt{2}),0)\)で最大の速さ:
$$v_{u}=Q\sqrt {\frac {2k}{(a+a\sqrt{2})M}}$$ をとる。
点電荷の作る電位と電場まとめ
・【電位はスカラー、電場はベクトル】をしっかり分けて理解して軸の設定と符号を間違えないように気をつける!
・電位Vが0=電気的な高さが0=運動が止まる
・電場Eが0=電気的な傾きが0=加速しない=最速点
・今回は、電気分野と力学分野の融合問題の中でも比較的有名で基礎レベルの融合問題でした。(計算は少し煩雑でしたが。)
・しかし、磁気と力学の融合問題などでは、点電荷が3次元空間をらせん運動をするなどグッと難易度が上がってきます。>>「力学が苦手な人〜難関大レベルまでの解説記事総まとめ!」<<
・電気分野のうちに、力学の復習も兼ねて見直しに力を入れておきましょう。
続編 (コンデンサ)と電磁気まとめ
点電荷の次の記事>>「コンデンサーの仕組みと公式の意味」を読む。
今回も最後までご覧いただき、有難うございました。
お役に立ちましたら、SNSでシェア&Twitterのフォローをお願いします。
質問・誤植・記事リクエスト等はコメント欄へ、その他のご依頼・お問い合わせはお問い合わせページよりお願い致します。

