
ベルヌーイ分布と二項分布
〜統計学入門【三】〜
<この記事の内容>:離散型の確率分布の中でも”もっとも基本的”な『ベルヌーイ分布』と、
・ベルヌーイ試行を複数回行う際に適用する『二項分布』について、
それぞれの意味、期待値・分散・標準偏差などを解説しています。
目次(タップした所へ飛びます)
ベルヌーイ分布とは
上述した通り、ここでは確率分布の中でも最も基礎的な、”離散型”かつ”1変数”である「ベルヌーイ分布」に付いて具体的に解説していきます。
”ベルヌーイ”の名前の由来となった、ヤコブ・ベルヌーイは確率・統計などと非常に興味深い関連があるので、ぜひ1度>>「ネイピア数e(自然対数の底)の意味/応用と数学者たちによる誕生の物語」<<をご覧ください。)
では、本題に戻ります。
ベルヌーイ試行とトランプ
今、1〜K(13)までの数字が書かれたトランプ(絵柄は一種類とする)13枚がある。
このトランプの中から一枚引いて、絵札(J、Q、K)が出たとき1ポイントもらえて、1〜10までのカードが出たときは0ポイントだとする。(この様な試行を【ベルヌーイ試行】と言います)
この試行の確率分布表は以下のようになります。
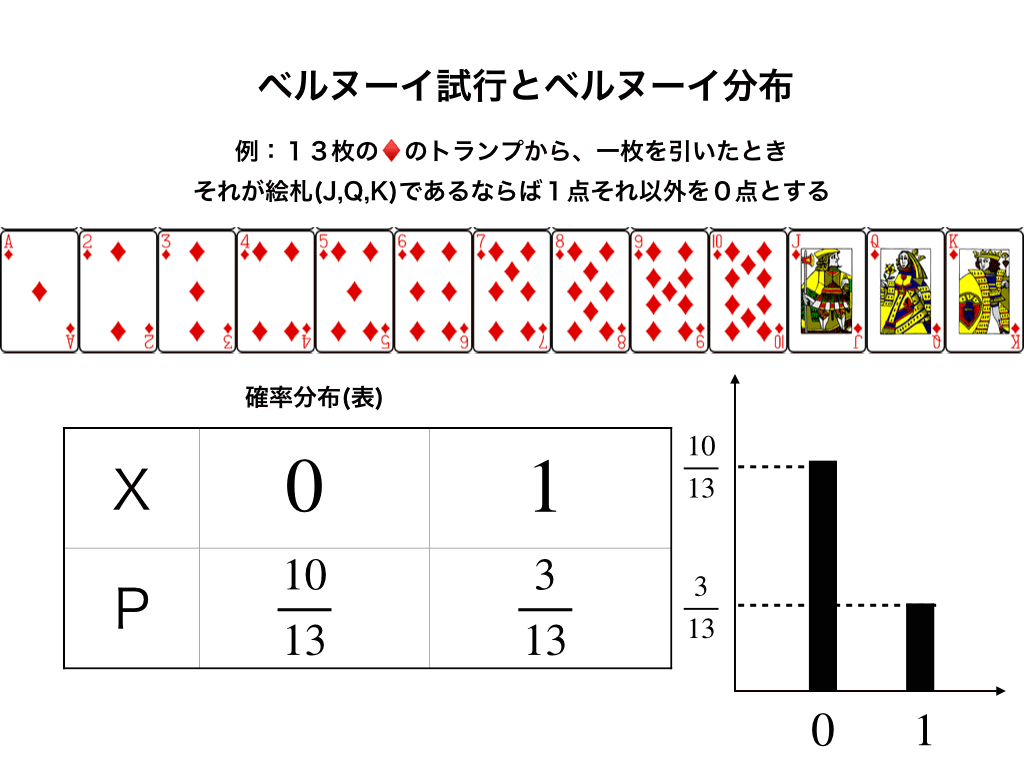
そして、この確率分布をもとに期待値、分散などを求めていきます。
ベルヌーイ分布の期待値/分散
期待値などについては、「演算子E (X),V(X),D(X)の性質や公式」も参照してください。
期待値:E[X]
期待値は確率変数・確率の総和によって求めることができ、これは『平均値』と同じ値となります。
今の例では、$$E[X]=0\times\frac{10}{13}+1\times\frac{3}{13}=\frac{3}{13}$$
これを一般化したものは、次に紹介する二項分布でのE(X),V(X)に\(n=1\)を代入すると求めることができます。
XがBe(p)にしたがうとき、(ここでのXは確率変数、”Be”はBernoulli分布の意味、pがある事象が起こる確率)
ベルヌーイ分布の\(E[X]=1\cdot p+0\cdot (1-p)\)
∴ E[X]=p
分散:V[X]
分散の定義は、(詳しくは「データの分析:分散と標準偏差 (2)」をご覧ください)
\(V[X]=E[X ^{2}]-(E[X]) ^{2}\)
\(=\{1 ^{2}p+0 ^{2}(1-p)\}-p ^{2}=p-p ^{2}\)
ではここまで学んだベルヌーイ分布を少し発展させた「二項分布」へと進みます。
二項分布とは
二項分布とは、簡単に紹介すると”ベルヌーイ試行”を繰り返した時の確率分布と言えます。
途中、”二項係数”や二項定理の知識が必要な場面が出てくるので、あやふやな方は「二項定理の基礎知識」←で解説しているので参考にしてください。
二項分布と反復試行の確率
先ほどのベルヌーイ分布と同じ題材で解説していきます。
13枚のトランプから1枚を取り出し、その数字を確認して元に戻す。
この試行を5回行ったとき、絵札を2回ひく確率を求めよ。
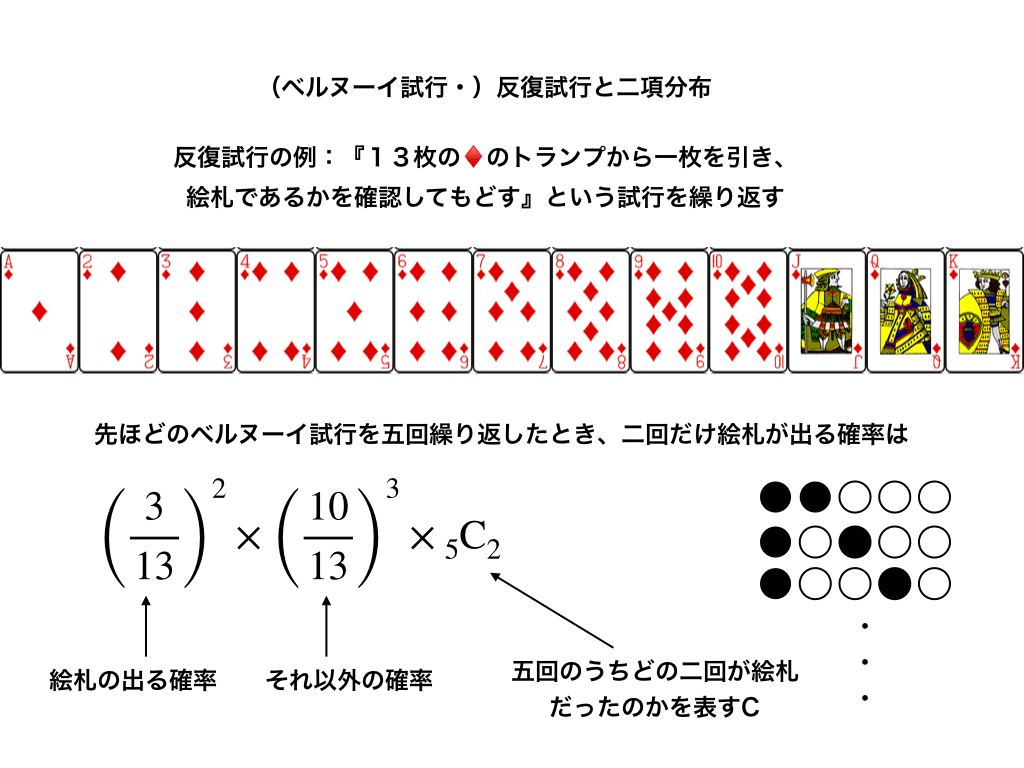
これは、高校数学Aで学ぶ『反復試行の確率』と言うものです。
$$\underbrace{5C2}_{どの2回?}\times\underbrace{(\frac{3}{13})^{2}}_{絵札をひく確率}\times\underbrace{(\frac{10}{13})^{3}}_{それ以外の確率}$$
これを一般化してみます。(かっこの中は具体例です。上の結果と照らし合わせながら読んでください。)
一回だけ試行した時なんらかの事象(絵札をひく)が起きる確率をp( \(\left(\frac{3}{13}\right)\) )とおく。
この試行をn回行う(5回)とき、この事象が\(X=l(回)\)起こる(2回)とする。
これを下の(図3)にまとめました。
$$n\mathrm{C}l\times(p^{l})\times(1-p)^{n-l}$$

上のような確率分布を”Bin(n,p)”、もしくは、”B(n,p)”で表します。(Binomial からとっています。)
二項分布の期待値/分散
ではここからは、二項分布での期待値・分散を見ていきます。
XがBin(n,p)にしたがうとき、
期待値
E[X]=np
分散
V[X]=p(1-np)
このそれぞれの導出法は、「積率母関数」の解説記事ができ次第、合わせて解説します。現在作成中。少々お待ちください)
ベルヌーイ分布と二項分布まとめ
今回学んだ内容のうち特に”二項分布”は、「正規分布(これは連続型)」につながる非常に重要度の高いものです。
初めて見た用語などもあるかもしれませんが、じっくり復習しておいてください。
統計学入門まとめ
統計学入門シリーズ
第一回:「統計学とは?イントロダクション」
第二回:「確率変数と確率分布のキソ」
第三回:「(今ココです)離散型確率分布の基本(ベルヌーイ&二項分布)」
第四回:「(標準)正規分布と連続確率分布」
最後までご覧いただきまして、有難うございました。
【総合学習メディア】:「スマナビング!」では,読者の皆さんのご感想を募集しています。ぜひコメント欄にお寄せください。
(※:個々の問題・証明の質問等には対応出来ない場合があります。)
・その他の「お問い合わせ/ご依頼/タイアップ」等に付きましては、【運営元ページ】よりご連絡をお願いいたします。

