
弱酸・弱塩基のpH(水素イオン指数)計算と電離平衡
この記事では電離度αが小さい、いわゆる「弱酸・弱塩基」の水素イオン指数(:pH)の計算法をイラスト付きで解説します。
苦手とする人が多い『電離平衡』に関しても詳しく説明しているので、ぜひじっくりとご覧ください。
(前回の「(強酸・強塩基)の水素イオン濃度とpHの計算」からご覧頂くと、よりスムーズに理解が進みます。)
目次(タップした所へ飛びます)
電離度αが小さい酸・塩基のpH(水素イオン指数)
はじめに、pHの求め方と計算方法について簡単におさらいしておきます。
pH計算のおさらい
pHは酸が放出した水素イオン\(H^{+}のモル濃度:[H^{+}]と書きます。\)を使って
\(pH=-\log_{10}{[H^{+}]}\)で求めることができます。
例えば、水素イオン濃度が10-3(mol/L)であれば、$$pH=ー\log_{10}{10^{-3}}=3\log_{10}{10}$$
より、pH=3、となります。
対数計算については→「常用対数と対数の性質の解説記事」を参照してください。
弱酸と電離度αの意味
「浸透圧の求め方の解説」等でも触れているのですが、
電離度(αで表されます)とは、化合物が溶媒中でどの程度電離するのか、
を0(全く電離しない:非電解質)〜1(100%電離)で表したものです。
強酸は、H +を多く放出するのでαは1に近く、弱酸は逆にほとんどH+を放出しないので、
αの値は非常に小さいです。
強酸・強塩基のpHの求め方は前回解説しましたが、弱酸・弱塩基の場合は求め方が少し異なります。
その理由は、放出(or受け取る)[H+](水素イオン濃度)がα=1の場合は<図1>のように簡単に考えられるのに対して、
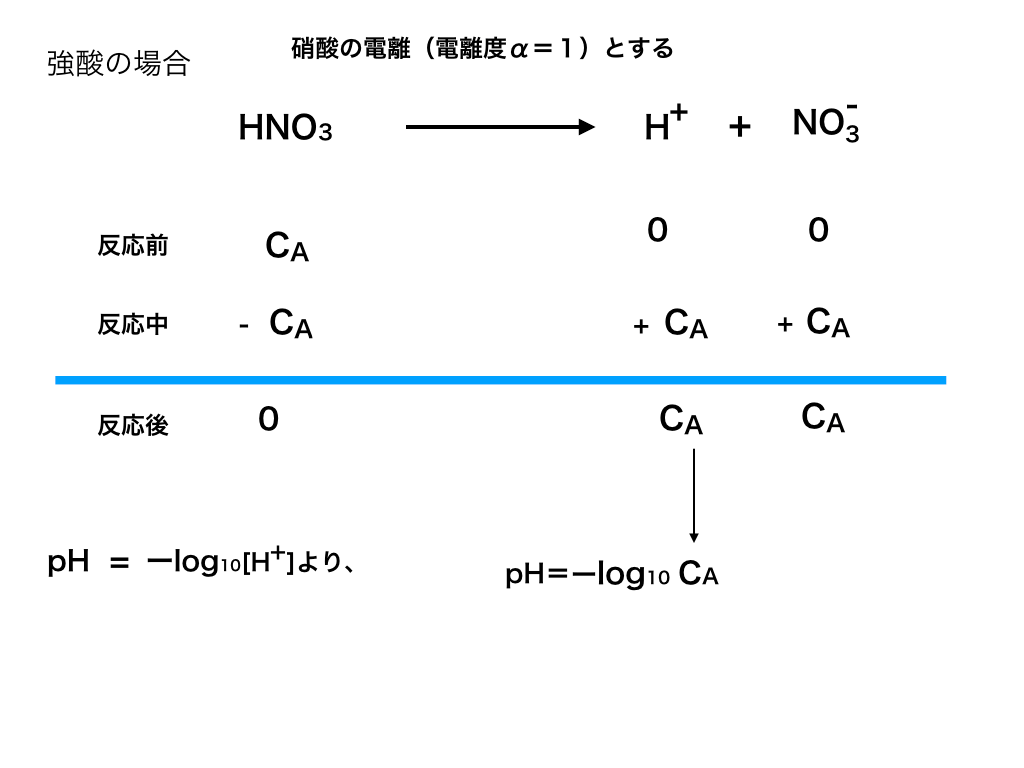
<図1:強酸の電離>
αが小さい時は“電離平衡”が関わってくるからです。
電離平衡と電離定数とは
弱酸(塩基含む)は、強酸・強塩基のように正反応(反応物から生成物への反応)
(例:H2SO4→2H++SO42ー)だけを起こさず、
逆反応(生成物から反応物に戻る方向)も同時に起こすことがあります。
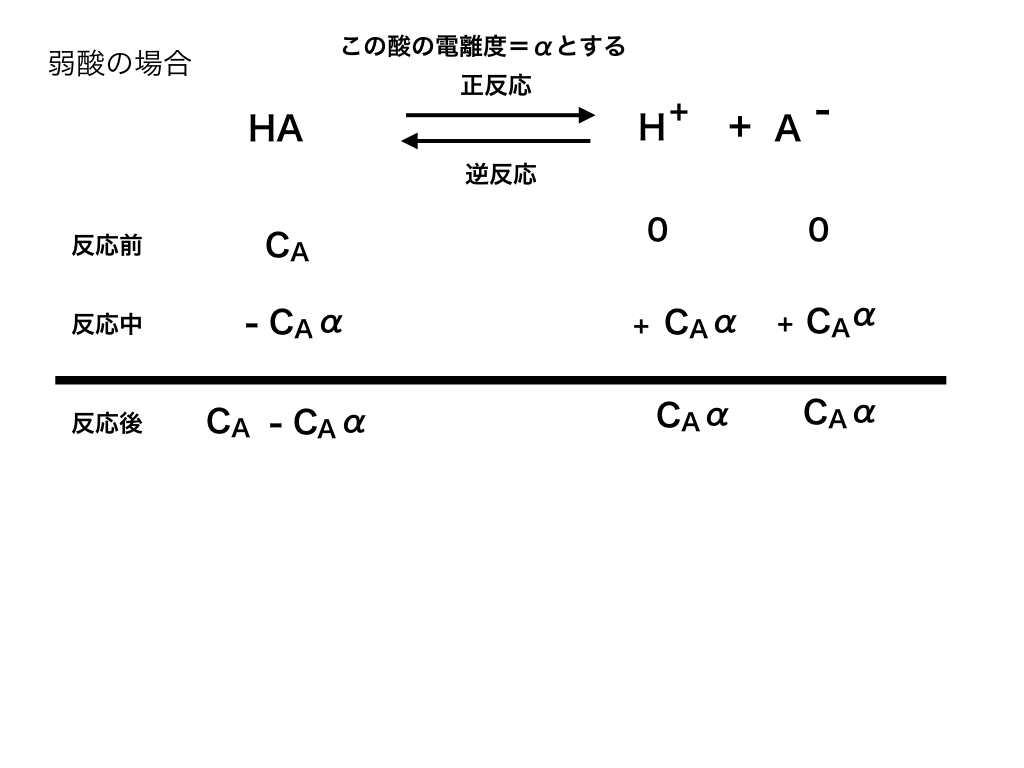
<弱酸の電離>
このように、正反応によって生成される物質(ここでは、H+とAー)と、
逆反応によって反応物に戻る(HA)速度が同じになった時、「見かけ上は」反応が終了(停止)したように見えます。
(実際には、上記の通り正反応・逆反応ともに起きています)
この状態を「化学平衡」と呼び、特に今回のように「電離」が関わる際には「電離平衡」と呼ばれています。
参考記事:「化学平衡とは?(濃度)平衡定数Kcを0からわかりやすく解説!」
では実際に、どのようにして弱酸のpHを求めるのか、少し長くなりますが1価の酸「HA」を使ってみていきましょう。
電離(平衡)定数Ka
電離平衡も化学平衡の一種ですので、電離定数と呼ばれるものが存在します。
今仮に、HAという1価の酸が存在する時、
$$電離定数Ka=\frac{[H^{+}][A^{-}]}{[HA]}\cdots(※)$$で求まります。
HAのモル濃度を\(C_{A}、電離度を\alpha\)とした時、上の(※)式より、
$$Ka=\frac {C_{A}\alpha× C_{A}\alpha}{C_{A}-C_{A}\alpha}$$
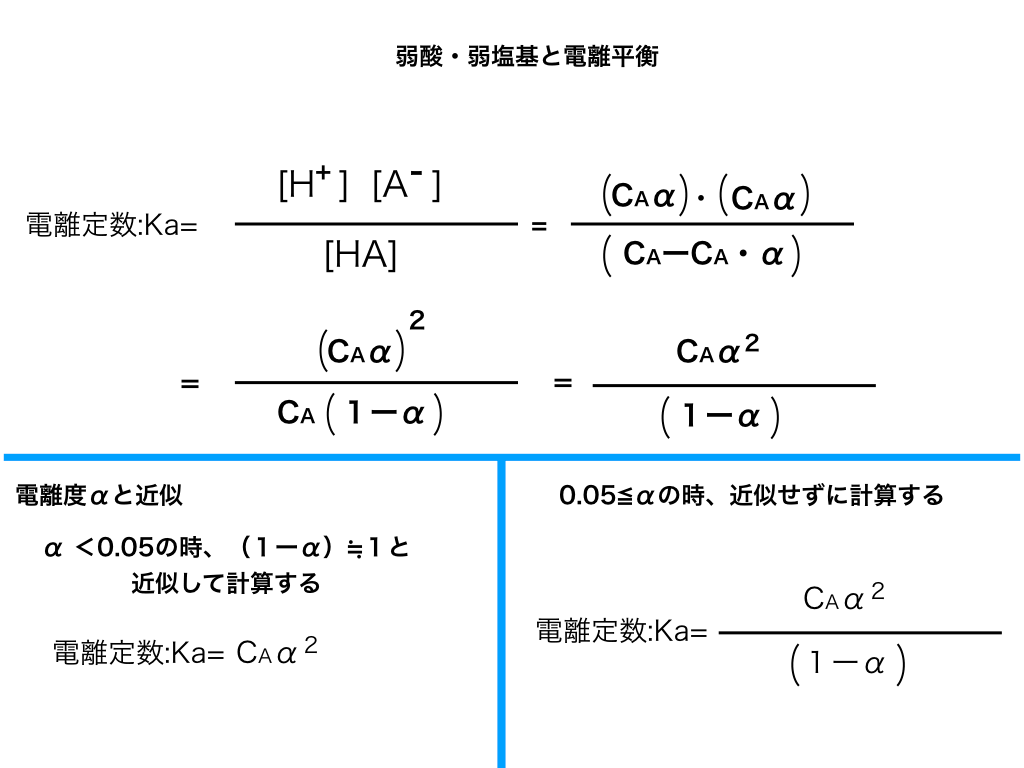
$$Ka=\frac {(C_{A}\alpha)^{2}}{C_{A}(1-\alpha)}$$
$$Ka=\frac {C_{A}\alpha^{2}}{1-\alpha}$$
電離度αを求める
次に、電離度αを求めていきます。電離度が小さい、弱酸・弱塩基ではαの求め方が2通りに分かれます。
α<<1の時:近似を使ってαを求める
ここで、分母に(1ーα)があります。αが1より十分小さい時、
「(1ーα)≒1」という近似が適用でき、
\(Ka=C_{A}α^{2}より、α^{2}=\frac{Ka}{C_{A}}\)
\(\Rightarrow α =\sqrt {\frac {Ka}{C_{A}}}\)
このようにして、αを求めることができます。
また、逆にαとモル濃度から電離定数を求めたり、αと電離定数からモル濃度を求めることもあるので、
これらの式を自由自在に使えるようにしましょう。
(1-α)に近似が適用できない時
具体的には、電離度αが0.05未満の場合、上の近似が適用できません。
その際には、以下のような手順でαを求めていきます。
まず、先ほどの$$Ka=\frac {C_{A}α^{2}}{1-α}$$の式から出発します。
近似が適用できないので、両辺に(1-α)をかけて分母を払います。
\(Ka(1-\alpha)=C_{A}\cdot \alpha^{2}\)
\(K_{a}-Ka_{\alpha}=C_{A}\alpha^{2}\)
この式を、0=の形にすると電離度αについての二次方程式となります。
\(C_{A}α^{2}+Kaα-Ka=0\)ここで、二次方程式の解の公式より、
$$α=\frac {-Ka\pm \sqrt {( Ka) ^{2}+4C_{A}Ka}}{2C_{A}}$$
電離度は正なので、分子の±は+になり、
$$α=\frac {-Ka+ \sqrt {( Ka) ^{2}+4C_{A}Ka}}{2C_{A}}$$
にKa,C_{A}を代入することによって近似が使えない時の電離度αを求めることができます。
さて、ここまでの流れはかなり複雑だったと思います。
以下のイラストで少し整理した上で、総まとめ問題で応用問題まで解けるように慣れていきましょう。
ここからは、例題を通して知識の整理をしていきましょう。
総まとめ用例題
今、HAという1価の酸があり、これを溶媒である水に溶かすと以下のように電離平衡する。
HA⇄H++A-
このHAの0.02(mol/L)水溶液の電離度αは0.02(25℃)であるとする。
また、電離定数:Kaは酸の濃度にかかわらず、同一温度では常に同じ値をとるものとし、(一)(二)ともに25℃のまま温度変化しないものとする。
(一)この酸の0.05(mol/L)水溶液のpH(水素イオン指数)を求めよ。
(二)この酸の0.05(mol/L)水溶液を水で100倍に希釈した時の電離度α’を求めよ。
解説
(解答解説一):この問題は単なる掛け算です。
\(pH=ー\log_{10}{[H+]}\)
より、[H+]を求めればよいので、
水溶液のモル濃度をCAとして、
\(C_{A}×α=0.05×0.02=0.001=10^{-3}\)
\(pH=-\log_{10}{10^{-3}}=3\) よって、pH=3。・・・(答)
(解答解説二):ここからが本題です。
電離度が0.05未満と仮定して計算する
この電離度α’は基準となる0.05未満なのか、それとも0.05より大きいのか判断がつきません。
そこで、とりあえずα’が0.05以下と『仮定』して、$$α =\sqrt {\frac {Ka}{C_{A}}}$$で近似値を求めてみます。
上の式で必要なK_{a}が求まっていないので、\(Ka=C_{A}×α^{2}より\)
\(Ka=5×10^{-2}×(2×10^{-2})^{2}\)
\(Ka=20×10^{-6}=2×10^{-5}\)
希釈しても電離定数は変わらない
問題文にあるように、同一温度ならば【電離定数の値が変わらない】ことを利用して、
$$α=\sqrt {\frac {2×10^{-5}}{5×10^{4}}}$$
これを計算すると、電離度α=0.2となります。
これは、初めの仮定α≦0.05に反するので、
近似ではなく厳密に(二次方程式を解いて)求める必要があることが分かります。
近似が使えない→α'についての二次方程式を解く
<近似が使えない時>の式、つまり
$$α '=\frac {-Ka+\sqrt {Ka^{2}-4Ka\cdot C_{A}}}{2C_{A}}$$を利用して
与えられた、CAとKaをそれぞれ代入していくと
α'=
$$\frac {-2\cdot 10^{-5}+\sqrt { (2\cdot 10^{-5}) ^{2}-4\cdot 2\cdot 10^{-5}\cdot 5\cdot 10^{-4} }}{2\cdot 5\cdot 10^{-4}}$$
$$= \frac {-2×10^{-5}+\sqrt {( 4×10^{-8}) ( 1+10^{-2}) }}{10^{-3}}$$
$$=( \frac {-2}{100}) +\frac {( 2× 10^{-4}) × \sqrt {\frac {101}{100}}}{10^{-3}}$$
$$= \frac {-1}{50}+\frac {1}{5}× \frac {\sqrt {101}}{10}$$
$$= \frac {\sqrt {101}-1}{50} ≒0.1809より$$
問2の電離度α'=0.18 ・・・(答)となります。
次回「逆滴定」と酸塩基反応の関連記事へ
かなり計算がヤヤコシイ問題でした。
計算に慣れておくのはもちろん、文字で解答させられる場合もあるので、どのようなタイプの問題でも解ける様に、問題集や過去問で類題を探して訓練しておきましょう!
次回は酸・塩基の中和滴定、特に逆滴定について解説していきます。
酸・塩基反応シリーズ
第二回「(強酸・強塩基の)水素イオン濃度とpH(水素イオン指数)の求め方」
第三回「今ここです」
第四回:作成中「酸塩基の中和滴定(逆滴定)」
今回も最後までご覧いただき有難うございました。
このサイトは皆さんの意見や、記事のリクエスト、SNSでの反応などをもとに日々改善・記事追加更新を行なっています。 そこで
・記事リクエストと質問・ご意見はコメント欄にお寄せください。可能な限り対応します。
・また、多くの学生・受験生に利用して頂くためにSNSでシェア(拡散)&当サイト公式Twitterのフォローをして頂くと助かります!
・より良いサイト運営・記事作成の為に是非ご協力お願い致します!
・その他のお問い合わせ/ご依頼等はお問い合わせページよりお願い致します。

