相対速度・加速度と応用問題
<この記事の内容>:「”鉛直”投げ上げ運動と3つの公式」「斜方投射と軌道の式」に続く第三回として、『相対速度/加速度』の見方を解説し、空中で2つの物体が衝突する、いわゆる『モンキーハンティング』の問題を通して知識の定着を図ります。
目次(タップした所へ飛びます)
相対速度・加速度とは?【相手ー自分】
二物体が運動している時、一方の物体からもう一方を見て(相対的に)問題を解くことがあります。実際に相対運動の例題を解きながら、計算の仕方や意味を見ていきます。
相対”速度”の意味とイメージ
さて、『相対』速度(+加速度)といっても特別難しい事ではありません。
たとえば、時速30km/hの列車に乗っている時、後ろからきた時速80km/hの特急電車に追い越されるとします。
特急列車は80km/hではなくもう少し遅い50km/hで追いつき、追い越していくように見えます。このように、相手に対して、自らの(正確に言うと観測する方から見た)速度を『相対速度』と言います。
相対速度の求め方
上の見出しにも書いていますが、”相対”ときたら→『相手ー自分』or『相手ー観測者』の式で計算します。
この引き算の順番をしっかり理解しておかないと、全く違う値になってしまうので、必ず頭に入れておきましょう。(もし忘れたら、先ほどの電車の例を思い出してみて下さい!)
相対”加速度”の意味と小まとめ例題
相対”加速度”も考え方、計算の仕方ともに相対”速度”と同じです。
【相手の加速度ー自分(観測者)の加速度】が『相対加速度』となります。
例題(直線上とベクトルを使う平面上の運動)
(ここでは、速度の分解を考えるために”ベクトル”を使用します。未習の方は「物理(基礎)に必要な最低限のベクトル講座」を先にご覧ください。)
(一): 今、<図Ⅰ>同一直線上に10(m/s)で移動する\(球_{M}\)と20(m/s)で同方向に移動する\(球_{m}\)がある。
\(球_{M}から球_{m}\)を見たときの相対速度を求めよ。
(二): (一)の\(球_{M}\)の加速度が\(5(m/s^{2})\)、\(球_{m}\)の加速度が\(10(m/s^{2})\)で加速し出したとき、\(球_{m}\)から見た\(球_{M}\)の相対加速度を求めよ。
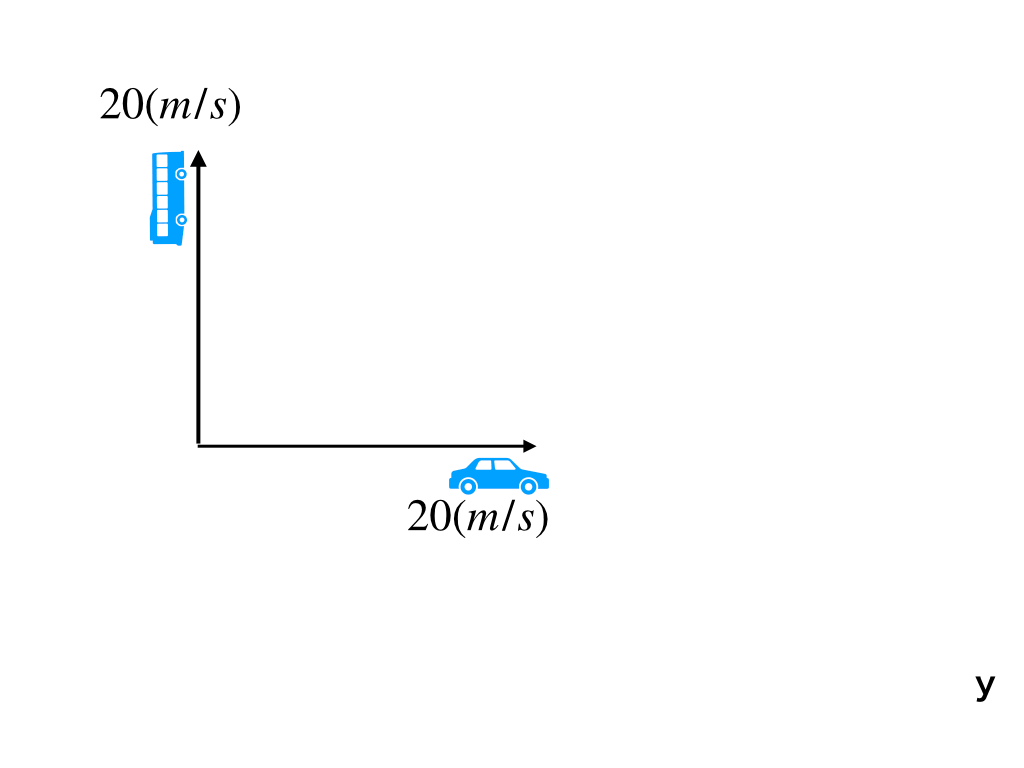
(三):<図Ⅱ>の車から見たバスの相対速度を求めよ。
解答解説(例題一)〜(三)
(三)以外は、【相手-自分】の考え方(見る物体を『自分』とする)で簡単に解けるはずです。
(一):Mからmより、\(20-10=10(m/s)\)
(二):mからMより、\(5-10=-5(m/s ^{2})\)
(三):下の図のように、x軸からy軸に135度の向きに\(20\sqrt{2}(m/s)\)
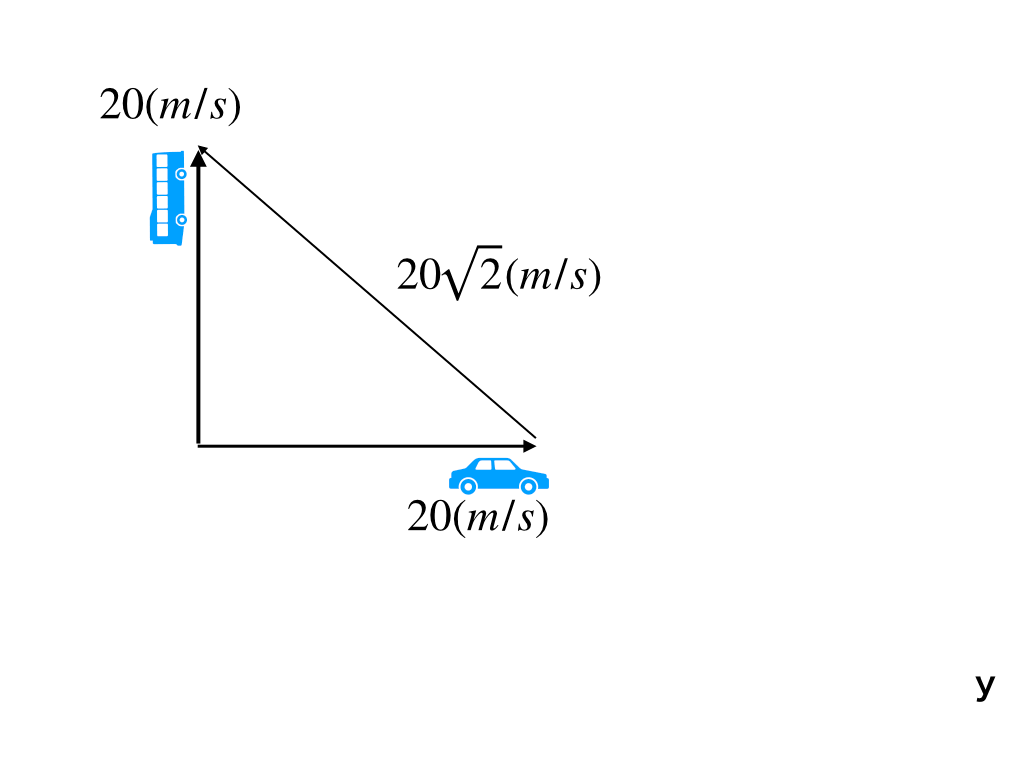
問題はこの(問三)です。進む方向が違うので、単純な引き算では相対速度を求める事ができません。
ここで「ベクトル」:【相手の速度ベクトルー自分の速度ベクトル】を図と三角比を用いて計算します。
(実は問一、二もベクトルの引き算だったのですが、同じ方向だったために普通の引き算として計算していました。)
2物体の等加速度運動(+衝突)
ここでは、先ほどの相対運動から有名・頻出の問題である、平面(実際には空間ですが、奥行きは考えないものとします)での二物体の衝突の問題(モンキーハンティング)を解いていきます。
モンキーハンティングの問題
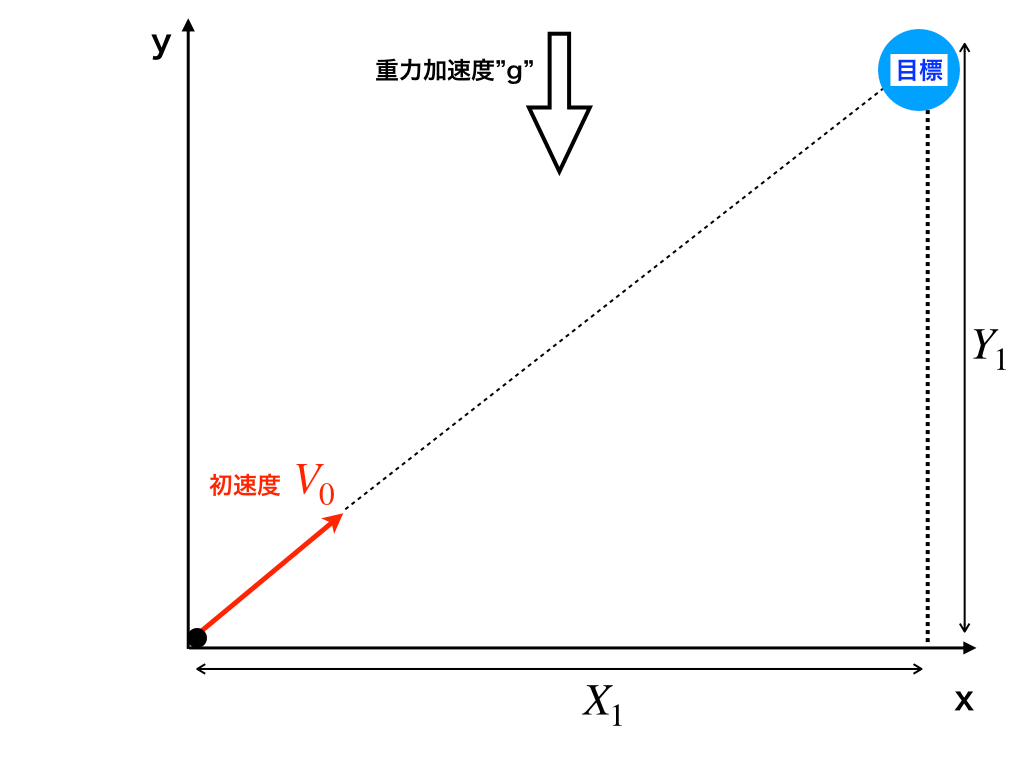
今、以下の図のようにx軸とy軸が交わる原点部分から初速度\(V_{0}、x軸から仰角\theta\)でまっすぐ矢を放った。目標物がそれと同時に高さ\(Y_{1}\)の位置から自由落下を始めた。
重力加速度を\(g(m/s^{2})\)として、次の各問いに答えよ。
(1):矢を放ってからt秒後の水平・鉛直方向の速度をそれぞれ求めよ。
(2):目標物のt秒後の水平・鉛直方向の速度をそれぞれ求めよ。
(3):目標物から矢の運動はどの様に見えるか。
+α:y座標の条件(追記中)
回答解説と考え方のコツ
まず問題の順番どおりに、それぞれの物体の位置(座標)を時間tで表し、【それが一致する⇔衝突】という考え方をして解いていきます。
(一):任意の時刻での『矢』の速度
V_{0}は斜方投射されているので、速度をx軸とy軸の成分に分解する必要があります。重力加速度に注意して、
\(v_{x}=v_{0}\cos\theta\)
\(v_{y}=v_{0}\sin\theta-gt\)
(二):任意の時刻での『目標物』の速度
この目標物は、《鉛直方向の落下》しかしないので、自由落下の公式より、
\(V_{x}=0\)
\(V_{y}=-gt\)
(三):相対運動
水平と鉛直方向のそれぞれに分けて、相対速度を計算します。その結果から、見え方を考察します。
\(v_{x}- V_{x}=v_{0}\sin\theta\)
\(v_{y}- V_{y}=v_{0}\cos\theta\)
この計算結果から、『等速度でまっすぐに矢が飛んでくる様に見える』ことがわかります。
+α:y座標の条件
上述した通り、矢と目標物の座標が一致すれば良いので、まず矢がX_{1}だけ進むのにかかる時間tを求めて、
$$t=\frac{X_{1}}{v_{0}\cos\theta}$$
それぞれのy座標を求め、
$$Y_{矢}=v_{0}\sin\theta \cdot t -\frac{g}{2}t^{2}$$
$$Y_{目標物}=Y_{1}-\frac{g}{2}t^{2}$$
\(Y_{矢}=Y_{目標物}\)より、
\(v_{0}\sin\theta \cdot t=Y_{1}\)
tを代入する。
$$\frac{v_{0}\sin\theta}{v_{0}\cos\theta}X_{1}= Y_{1}$$
$$\tan\theta=\frac{Y_{1}}{X_{1}}$$
これは初めの仰角θの条件なので、\(v_{0}\)がいくらであっても、命中することがわかります。
等加速度運動(3)まとめ
・なによりも『相手ー自分』を徹底的に身につけておきましょう。そうすれば多少問題がヤヤコシイ場合でも、確実に解くことができます。
物理・基礎の関連記事まとめ
等加速度運動第一回:「鉛直投げ上げと3つの公式」
等加速度運動第二回:「斜方投射と放物線の軌道を求めるコツ」
等加速度運動第三回:「(今ここです)」
今回も最後までご覧いただきまして、ありがとうございました。
【受験/学習メディア】:「スマホで学ぶサイト、『スマナビング!』」では,読者の皆さんのご意見・ご感想を募集しています。ぜひ、コメント欄までお寄せください。
(※:現在、個々の問題の質問等には対応出来ない場合があります。)
・その他の『お問い合わせ/ご依頼/タイアップ等』に関しましては、【運営元ページ】よりご連絡下さい。

