分数関数と無理関数の基礎〜応用
<この記事の内容と対象>:【0から学ぶorこの範囲が苦手な人を対象】に、分数関数・無理関数の式からグラフの描き方(漸近線・平行移動)の解説をしています。
後半では、グラフを利用して”無理不等式”、”分数方程式・不等式”を解く方法まで例題付きで紹介しました。
目次(タップした所へ飛びます)
分数関数とは?
さて、まずは分数関数とは何かについて極々簡単に説明すると、$$f(x)=\frac{●}{(xの式)}+△$$のように表される関数のことを言います。
言葉だけではわかりづらいので、実際にグラフを見ながら習得していきましょう。
グラフの描き方と式変形の仕方
まず、分数関数の(グラフ)には、基本中の基本となる$$f(x)=\frac{\pm k}{x}$$のカタチがあります。
基本となる2つのグラフ
上の式のk=1,y=f(x)としてx-y座標平面上にグラフを描くと次のようになります。
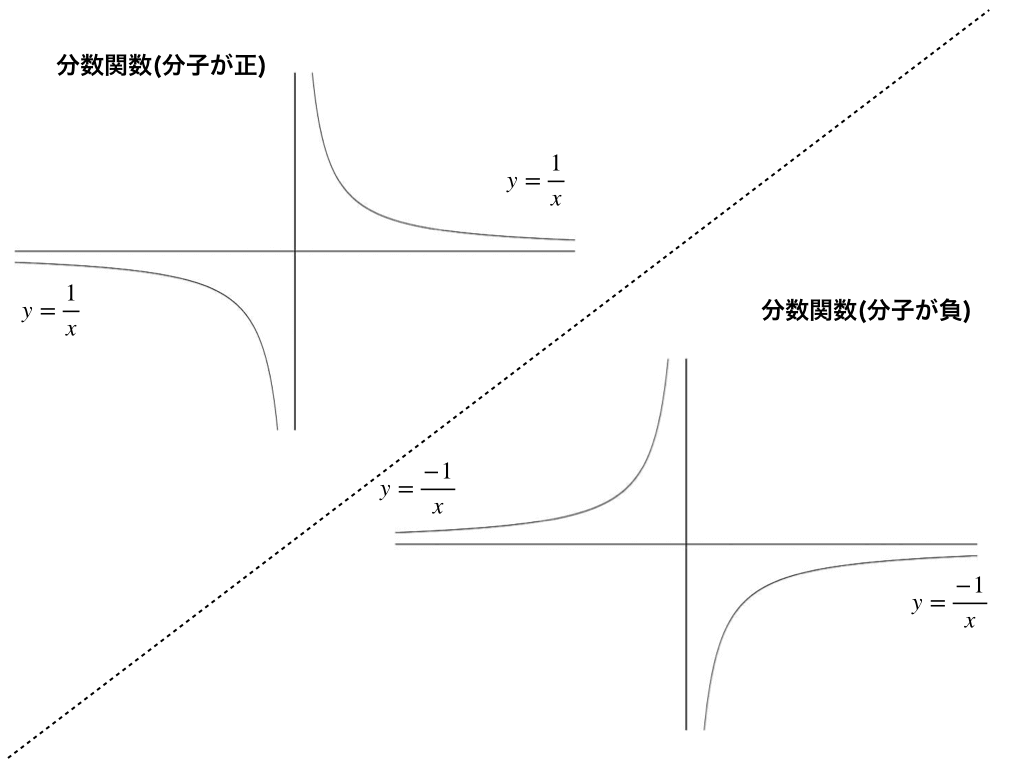
これは『反比例のグラフ』そのままですね!(実際、両辺に”x”をかけると\(xy=\pm 1\)となります。)
実践編(漸近線と平行移動)
基本のグラフがわかったところで、次にもう少しレベルアップした分数関数のグラフの書き方を習得しましょう。
・重要事項:とにかく基本の\(y=\frac{k}{(xの式)}\)のカタチに式変形する!
問題
問題:$$y=\frac{3x+2}{x+5}のグラフをかけ。$$
少しややこしく感じるかもしれないですが、実行することは『基本のカタチへ変形する』だけです。
分子から“x”を取り除いて平行移動をチェック
実際にやってみましょう。分子の”x”がじゃまなので、(分子の式)÷(分母の式)を行って、分子は数字だけになるようにします。(この割り算では、あまりが出ても構いません)
すると、\(3x+2=(x+5)\times (3)+(-13)\)となり、余りが-13、商が3となることがわかりました。
解答
上の計算より、$$y=\frac{3x+2}{x+5}=\frac{-13}{x+5}+3$$
ここで、分子が”負”かつ、分母がx+5であることより、x=−5は存在しない(分母は0になれない)ため、x=-5が漸近線のうちの一つです。
また、(x+5)はx軸負方向に5平行移動したことを意味します。(この辺りは、『二次関数などの平行移動』と考え方が一緒です。)
さらに、平行移動を考えると、y=(分数)+3なので、\(\frac{\pm k}{x}\)のグラフに比べて、”3”だけy軸正方向へ動きます。
ここで、もう一つの漸近線は「y=3」であることがこの式変形によってわかりました。
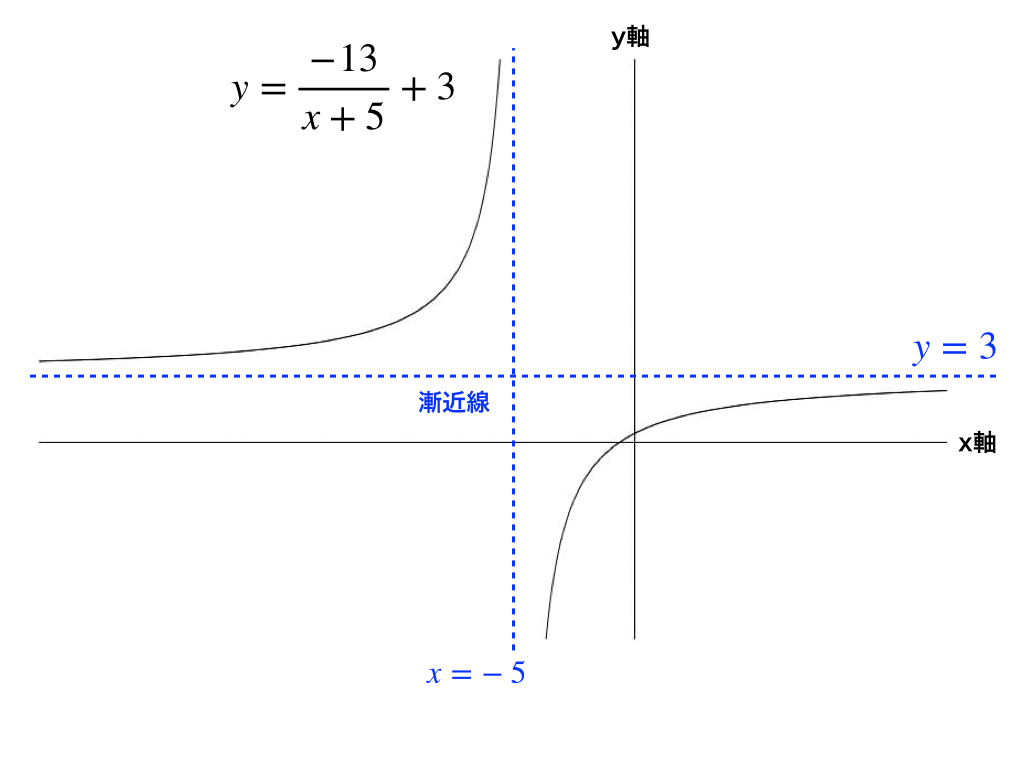
<答えのグラフ>
無理関数とは?
次は無理関数です。これも具体的なグラフを見ながら説明していきますが、簡単に言うと\(f(x)=\sqrt{(xの式)}\)になっている関数を言います。
4つの基本的なグラフ
無理関数のグラフには大きく分けて4種類あり、それらを下の図にまとめました。
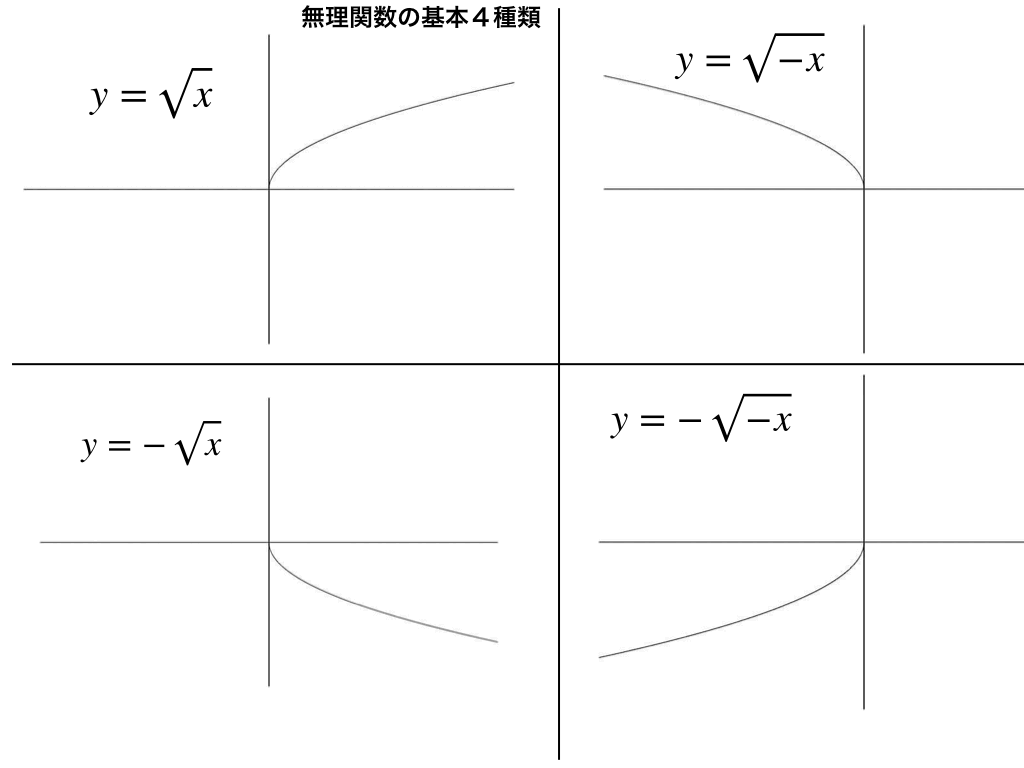
実践的な無理関数のグラフ
上のグラフを頭に入れておくと、あとは4種類から1つえらび、これから行う式変形によって平行移動させるだけでグラフを書くことができる様になります。
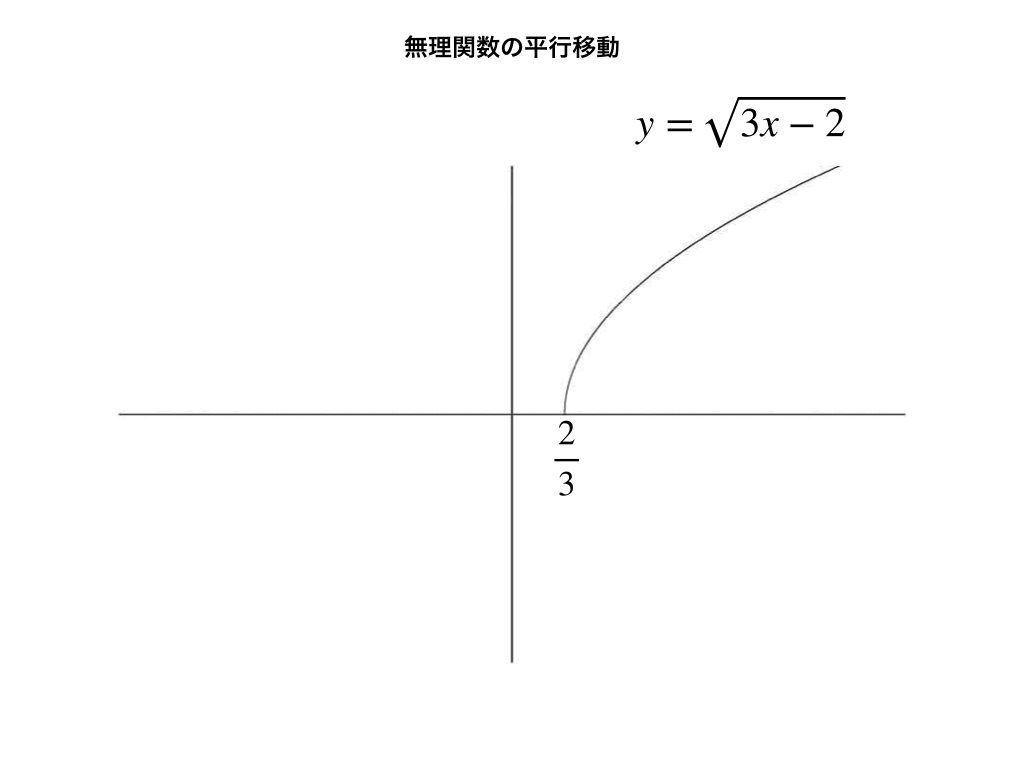
\(y=\sqrt{3x+2}\)これを3でくくると、
$$y=\sqrt{3(x-\frac{2}{3})}$$となって\(\sqrt{3x}\)をx軸正方向に2/3移動させたものであることが分かります。
分数/無理方程式と不等式
さて、ここまではそれぞれの関数とそのグラフの概要を見てきました。
ここからは、より実践的な方程式・不等式の解法を紹介していきます。
分数方程式/不等式
まずはじめに、分数関数が入った方程式・不等式です。
問題(一):次の方程式の解を求めよ。$$\frac{2x+6}{x+4}=2x$$
解き方:まず両辺に\((x+4)を掛けて(2x+6)=2x(x+4)\)この二次方程式を解くと、\(x=\frac{-3\pm \sqrt{21}}{2}\)。
よってこれが答えとなります。
分数不等式
問題(二):$$\frac{2x+6}{x+4}>2x$$を満たすxの範囲を求めよ。
解き方:先ほどのグラフの書き方と(一)を利用すると、下の様な状態であるので(青色の点線は漸近線、黄色の丸が交点)、分数関数の方がy=2xより上部にきているところを探します。
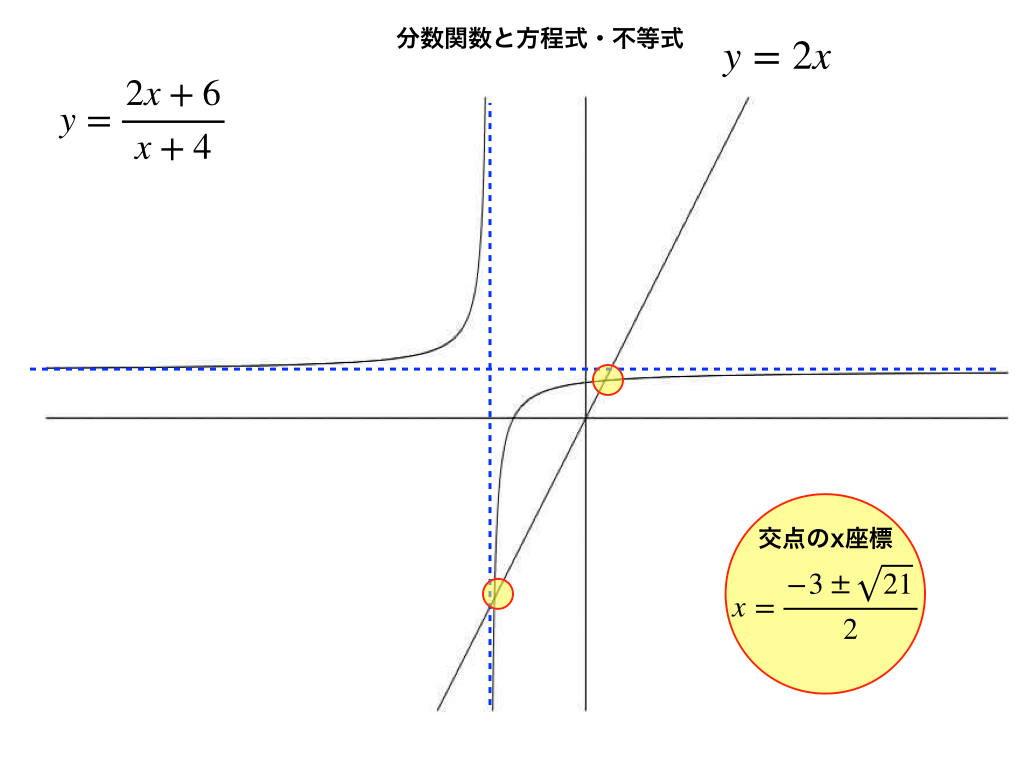
すると、x<ー4では常に条件を満たし、ー4<xの範囲では、【交点から交点までの間】のみ(分数関数)>y=2xとなるので、これらをあわせて
(答):$$x<ー4、\frac{-3-\sqrt{21}}{2}<x<\frac{-3+\sqrt{21}}{2}$$
無理不等式
無理関数にうつります。不等式の範囲を解く途中で方程式も解くことになるので、ここでは不等式一題のみ扱う事とします。
\(\sqrt{2x+5}>x\)の不等式を満たすxの範囲を求めよ。
まず交点を求めます。両辺を二乗して、\(2x+5=x^{2}\)よって、\(x=1\pm \sqrt{6}\)
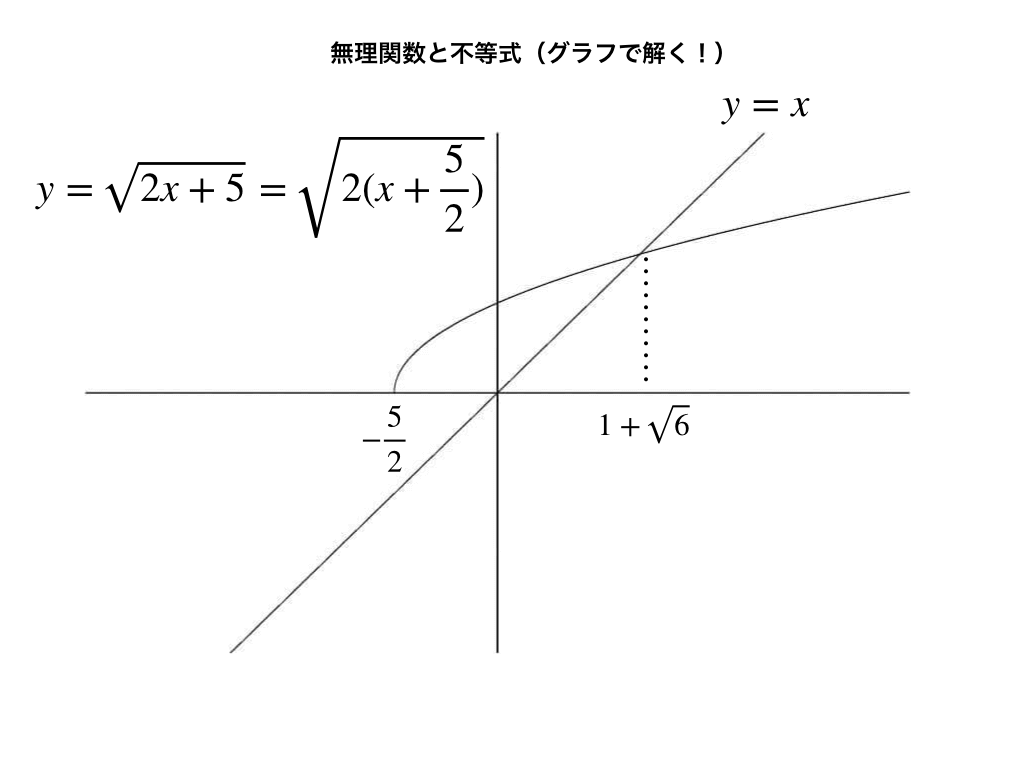
ここで、無理関数のグラフを以下の図の様にかくと、\(x=1ー \sqrt{6}\)では交点になりません。
よって1+√6のみが交点で、y=xよりもy=√2x+5が大きい範囲を探しているので、
$$-\frac{5}{2}<x<1+\sqrt{6}$$・・・(答)
まとめと応用編・関連記事へ
今回の内容自体はそれほど難しいものでは無かったかと思います。
しかし、これらの関数と微積分の融合や、難易度の高い「論証問題」などを扱う際に重要な要素であるので、基礎部分はしっかりと確認しておきましょう。
記事一覧と合成/逆関数へ
続編(2019/10/28NEW!):「”合成”関数と”逆”関数の求め方+特徴」
関連する記事や、あわせて読むと力が付く記事を集めました。
今回も最後までご覧いただきまして、ありがとうございました。
受験・学習メディア:「スマナビング!」では、読者の皆さんのご意見・ご感想の募集をコメント欄で行なっています。
(※:現在、個々の問題の解き方や証明については対応できない事がございます。ご了承ください。)
・その他の「お問い合わせ/ご依頼」については、【運営元ページ】よりお願いいたします。

