
色々な三角関数のグラフの描き方/式の読み取り(1)
<この記事の内容>:\(A \sin B(\theta \pm \pi)\)と言った、フクザツな三角関数の式を読み取ってそれをグラフにする方法をわかりやすく解説しました。
更にシリーズ(2)では、その逆に三角関数のグラフから、式を作る方法を紹介します(「(作成中)グラフを読み取り式を作る」)。
(物理の波動分野でも、「波の式」を作る時があり、方法が似通っているので→「高校物理:正弦波の式の作り方とコツ」も参考にしてください)
<併せて読んでおきたい記事>:「三角比・三角関数の基礎と重要公式まとめ」
目次(タップした所へ飛びます)
三角関数の基本的なグラフと式
まずはじめに、最も基本的な\(\sin,\cos,\tan\)の式→グラフを確認します。
正弦(サイン)のグラフ
\(y=\sin\theta のグラフ\)は、初め0からカーブを描いて\(\theta=\frac{\pi}{2}\)の時最大値1を取ります。
その後、\(\theta=\pi\) で0に戻りさらに減少を続けて\(\theta=\frac{3\pi}{2}\)で最小値-1、後は再び0\((2\pi)\)まで増加します。
\(y=\sin\theta のグラフ\)はこれを周期的に繰り返します。それを表したのが以下の《図1》です。普段のx軸が\(\theta 軸\)に変化していることに注意しましょう。
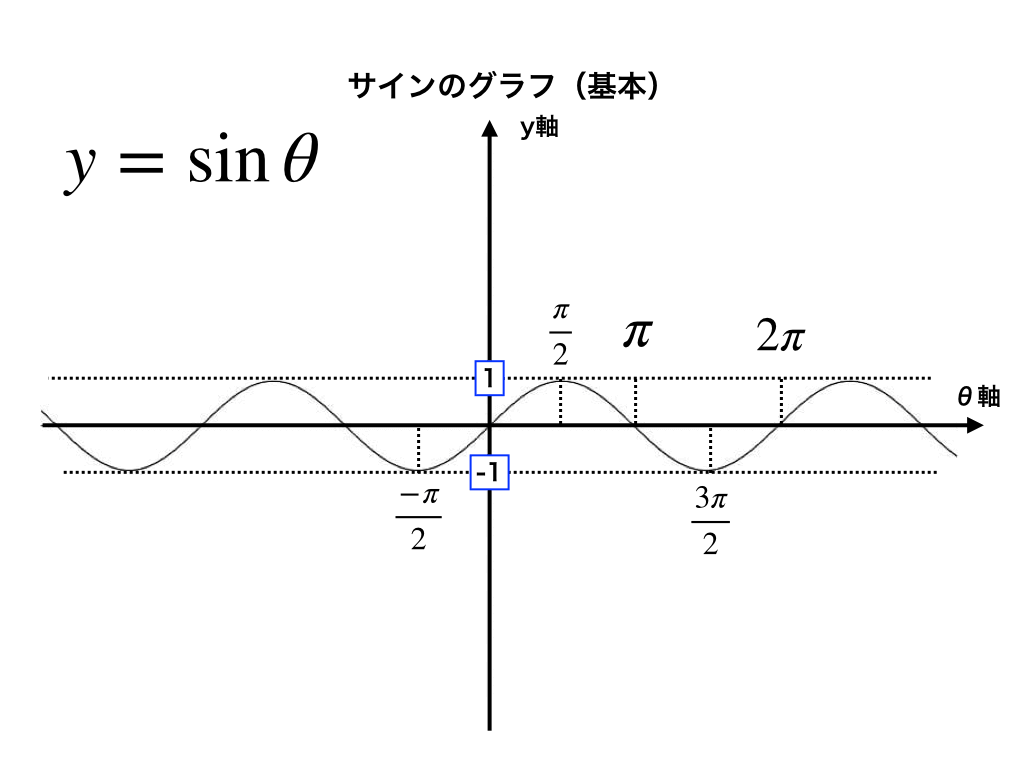
《正弦の図1》
グラフは単位円とともに考える
上の・・・→-3/2π(rad)→0(rad)→1/2π(rad)→π(rad)→3/2π(rad)→2π(rad)→・・・に対応する値は『単位円』を横に描いて、反時計回りに確認しながら進めましょう。
そうすると三角比(関数)の”値”と”グラフ”のつながりが理解しやすく、応用も効きやすいのでオススメです。
余弦(コサイン)のグラフ
\(y=\cos\theta のグラフ\)は、サインのグラフと違い”1”(最大値)からカーブを描いて\(\theta=\frac{\pi}{2}\)の時0となって、その後\(\theta=\pi\) で-1(最小値)を取ります。
ここからは増加し続け\(\theta=\frac{3\pi}{2}\)で0、後は再び”1”\((2\pi)\)に戻ることを延々と繰り返します。
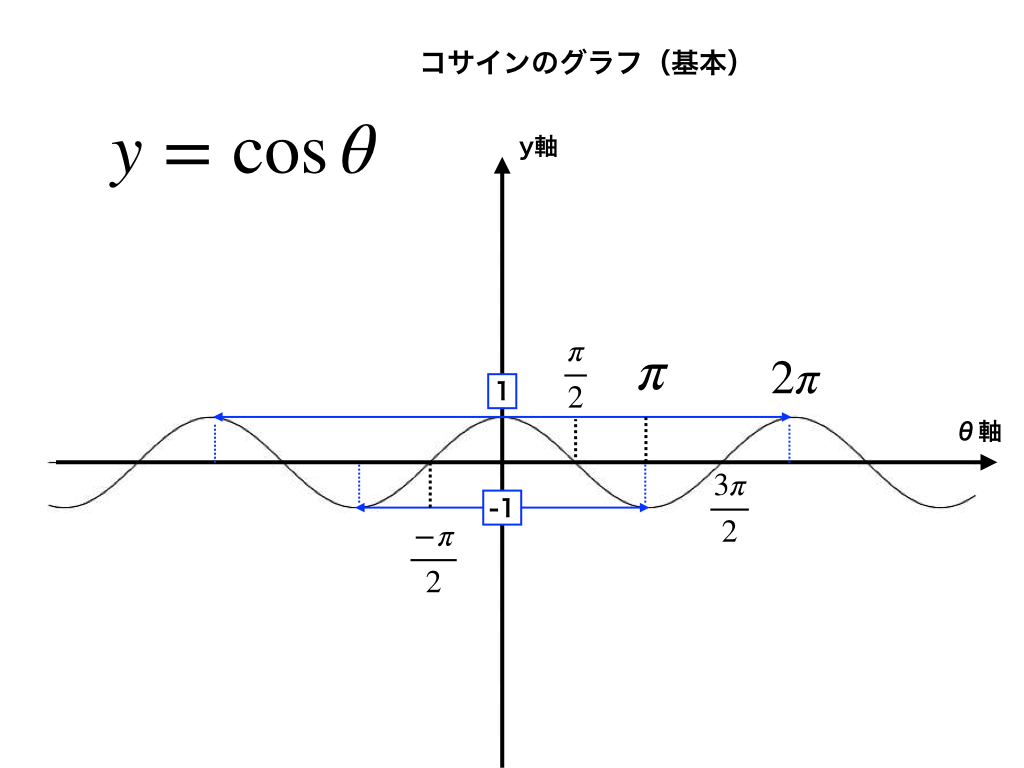
《余弦の図2》
(偶関数:奇関数と三角関数)
今後、積分などでとくに役立つ「偶関数と奇関数の種類と意味〜応用まで」に三角関数のサイン・コサインも当てはまります。
余裕があれば、ぜひ一度読んでおいてください!
正接(タンジェント)のグラフ【要注意】
\(y=\tan\theta のグラフ\)は、他の2つとはかなり違うので注意が必要です。タンジェントのグラフは、先に見てもらってから詳しく説明していきます。
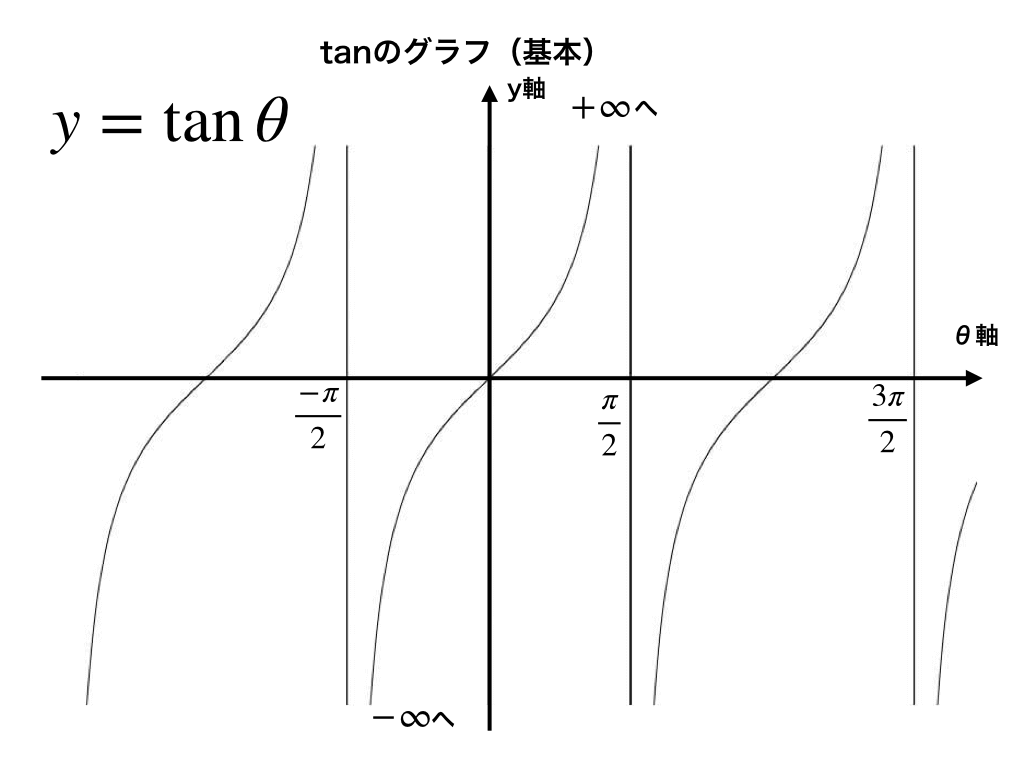
《正接(tan)の図》
そもそも$$\tanは、=\frac{\sin\theta}{\cos\theta}$$で表す事ができました。(参考:「三角比の基本・相互関係」)
そして、数学では”0”で割ってはいけないというルールが存在します。
・つまり、分母である『”cos”が0のところの値は存在しない』のです。
・また、詳しくは極限《数3》の範囲になってしまいますが、分母が0にはならなくとも、“限りなく”0に近い値をとる(ex:0.000・・・1)場合、分子をこの【小さな値で割る】ので全体としては∞へ向かいます。
したがって、\(\theta=\frac{\pi}{2}\)の倍数のとき(=つまり\(\cos\theta=0 \)となるとき)\(\pm∞\)へ限りなく近く=『漸近(ぜんきん)する』というグラフを描きます。
更に、「分子」は0になっても構わないので\(\sin \theta =0\)となる、0(rad)「←この時原点を通る」、π(rad)、2π(rad)・・・でy=0を通ります。
三角関数の式をグラフへ(応用)
次に、それぞれの関数の式を変化(周期・振幅・位相)させることで、グラフがどのように変化(移動・横に伸びたり、縦に伸びたり、etc,,,)するのか、【特に苦手な人が多い】所をひとつひとつ見ていきます。
振幅を表す部分とグラフ
「振幅」とはグラフの“高さ(縦方向の大きさ)”と考えてください。
(例1−1):\(y=2\sin\theta\)と
(例1−2):\(y=\frac{1}{3}\sin\theta\)を見てみましょう。
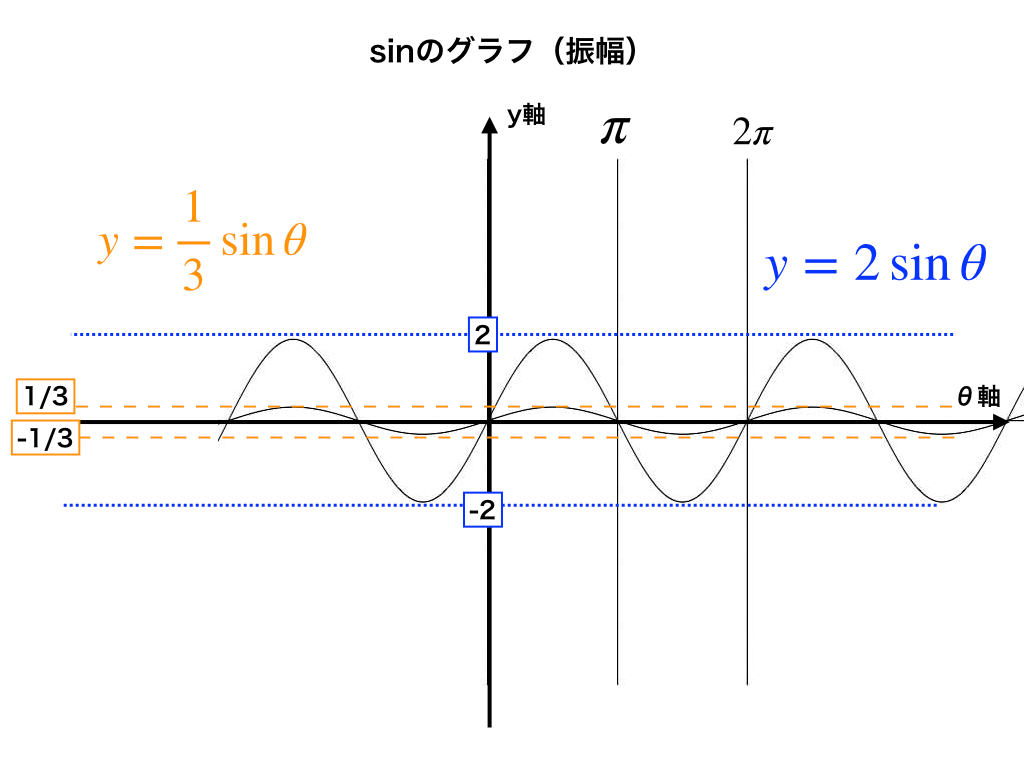
《振幅の例イメージ》
周期を表す部分とグラフ
「周期」とは(sin,cos)でグラフが一巡する長さ=“(横方向の大きさ)”のことで、これに影響するのは、\(sinB\theta \)のBの部分です。
こちらも例を挙げて視覚的に理解していきます。
(例2−1):\(\sin2(\theta)\)
(例2−2):$$\sin\frac{1}{2}(\theta)$$
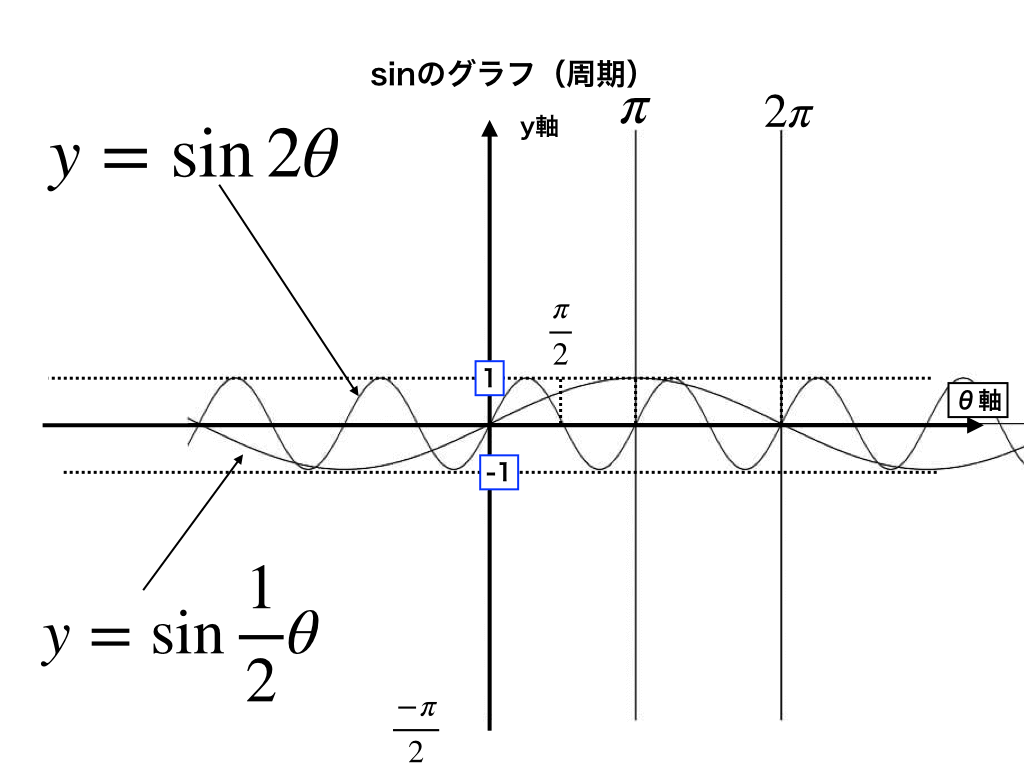
このように、(角度:弧度θ)の前につく係数の逆数倍、周期が伸びたり/縮んだりしている様子がわかります。
これも単位円をなぞりながら、『同じθであれば、\(\sin 2\theta\)のときには、\(\pi\)に付くために必要な\(\theta=\frac{1}{2}\pi\)ですむので、半分の期間で1周する』=『グラフの横が半分に縮むなぁ』といった事が実感できます。
位相の遅れ/進みを表す部分とグラフへの影響
「位相」はことばが少し難しいので、角度【弧度】の部分のことであると考えてください。
ex:\(\sin(\theta \pm \pi)\)などの所です。
ここでは、$$y=\tan(\theta+\frac{\pi}{6})$$を例に考えていきます。
普通の\(y=\tan\theta\)は以下の通りでした。(上の正接の項参照)

この(カッコの中)が、\(θ→θ+π/6に\)変わると以下の図の様に平行移動します。
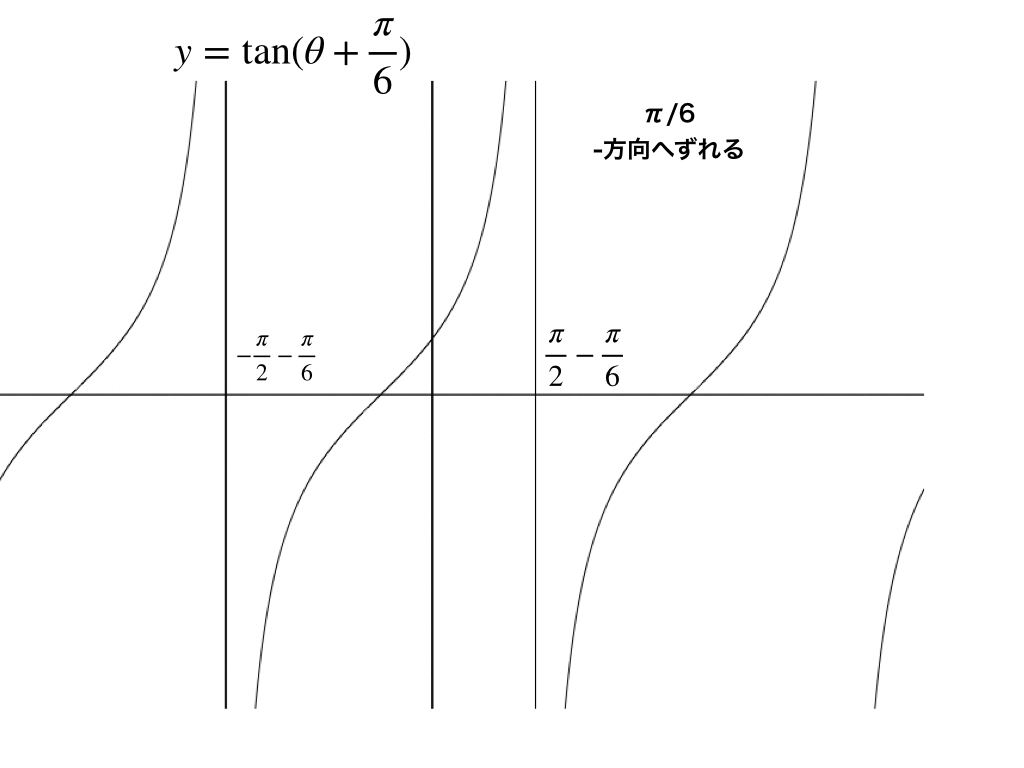
《正接のグラフの移動》
具体的に数値を入れて考えて見ましょう。
・θ=0→θ=π/6に、
・\(漸近線であるθ=π/2→(π/2+π/6=)4π/6=2π/3\)
逆に考えると、もとの式でθ=0のy座標にするには、θ=-π/6を代入しないといけないようになっています。
このように次々とグラフがθ軸【マイナス方向】へ移動していきます。
これは丁度、一次関数:y=ax+bを『y=a(x+c)+b』にした際、x軸負方向に”c”移動する事と同じ考え方です。
三角関数のグラフと式まとめと続編へ
・さて、今回は三角関数のグラフ⇔式の関係を解説しました。
・応用編で紹介した「3つ」は単独ででることは少なく、ほとんどの場合二つ以上を融合して出題されます。
・そのような場合(さらにフクザツになるので)にも対応できるように、それぞれをしっかり復習しておきましょう。
・次回(2)は、今回(1)の逆である「グラフ→式」と(1)、(2)両方の応用(融合)問題を解説します。
関連記事と次回へ
「(今ここです)第一回:三角関数の式→グラフを描く」
「(作成中):(第二回)グラフから三角関数の式を作る方法」
学習・受験メディア「スマナビング!」では読者の皆さんのご意見、ご感想を【コメント欄】で募集しております。
(※):現在個々の問題のご質問に関しては、時期的に対応できない場合がございます。
(その他の誤植の指摘や、ご感想は引き続き募集しています。)
・また、お問い合わせ/ご依頼/その他のご連絡については、【運営元ページ】よりお願いいたします。

