
余因子の求め方・意味と使い方(線形代数10)
<今回の内容>:余因子の求め方と使い方:余因子の意味から何の役に立つのか、詳しい計算方法、さらに余因子展開(これも解説します)を利用した行列式の求め方までイラストを用いて詳しく紹介しています。
<これまでの線形代数学の入門記事>:「0から学ぶ線形代数の解説記事まとめ」
2019/03/25更新続編:「余因子行列の作り方とその応用(逆行列の計算)を具体的に解説!」完成しました。
目次(タップした所へ飛びます)
余因子とは?その意味と求め方
はじめに、「余因子」とは何か?から説明していきます。文章にすると難しく感じますが、以下のイラストを見れば直感的に理解できるかと思います。
『余因子』とは、文字通り『(以下で説明する任意の行と列を取り去って)余った成分からなる行列の行列式にある規則に従って±をつけたもの』と言えます。
が、これだとよくわからないので、早速余因子を作りながらどういったものか理解していきましょう。
余因子の作り方(手順)
では、余因子を作る手順をイラストを使いながら解説していきます。ここでは、3×3サイズの行列:Aを例にして話を進めます。
$$A=\begin{bmatrix}
1 & 3 & 2 \\
2 & 2 & 1 \\
3 & 2 & 2
\end{bmatrix}$$
とします。
行列から任意の1行と1列を取り去る
まずこの行列Aから”どの”『行と列』でも良いので、図のように1行分と1列分を取ります。ここでは、3行目と2列目を取り除きました。すると、成分が4つ残ります。
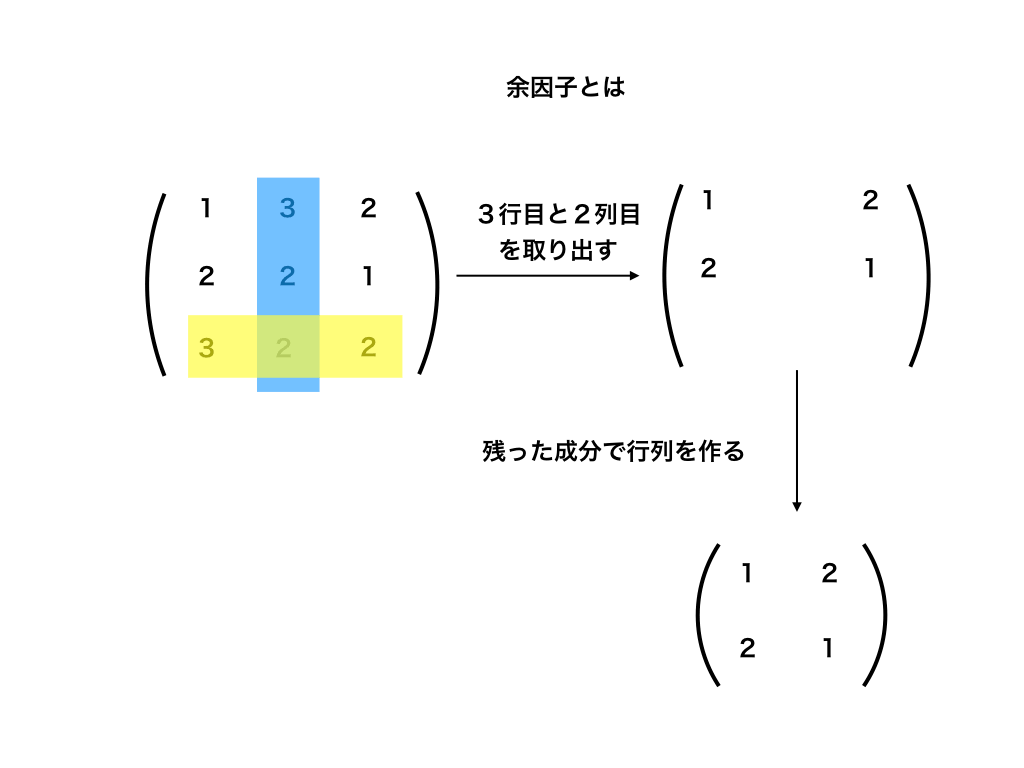
<余因子の作り方1>
残った行列の行列式を求める
次に、残った行列の行列式を計算します。この『残りの行列』を元の行列の文字Aに、
<取り去った行の番号と、列の番号を>添え字として、$$A_{行,列}$$のように表します。
$$A_{3,2}=\begin{bmatrix}
1 & 2 \\
2 & 1
\end{bmatrix}$$
この行列式を求めると<参考:「逆行列と行列式の求め方」>、
\(\det A_{3,2}=1×1ー2×2=-3\)
より、行列式は−3と求まりました。
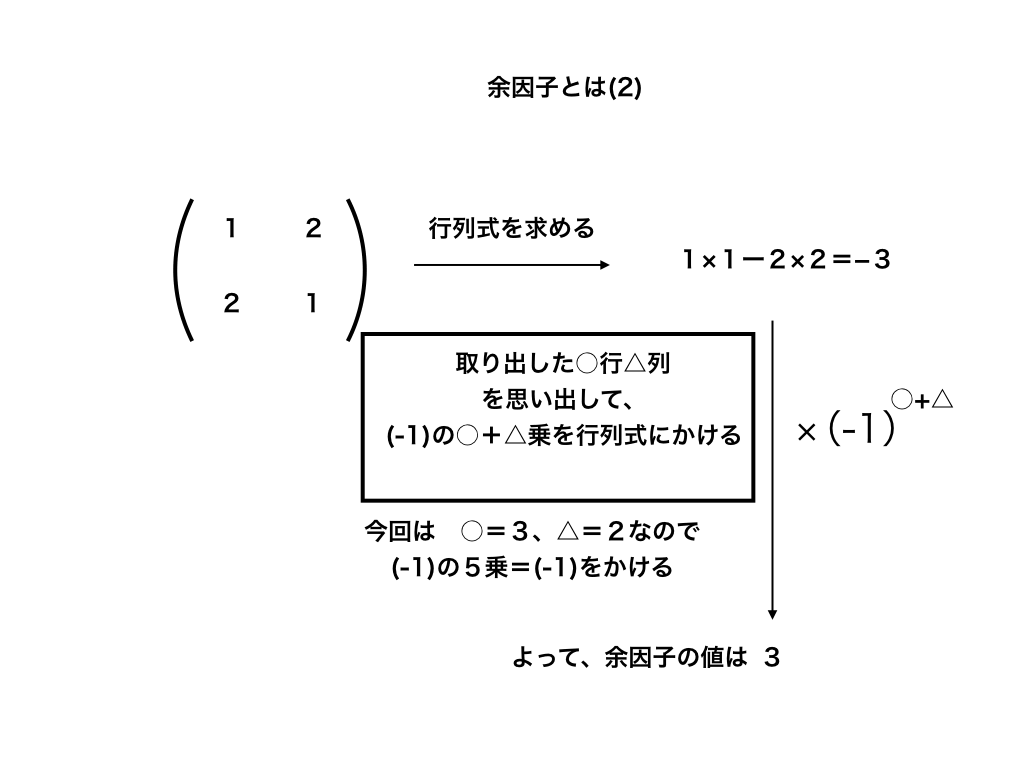
求めた行列式にある規則に従って±をつける
最後に、求めた行列式の\(A_{行,列}\)の『行』と『列』の添え字の部分に注意して、$$A_{行,列}×(−1)^{行+列}$$を計算すると余因子が求まります。
つまり、取り去った行の行数(ここでは3行目を取り去ったので『3』)、と、取り去った列の列数(ここでは2列目なので『2』)を足した数=『5』を計算します。
そして、(−1)の『5乗』を上で求めた行列式にかけることで余因子が求まります。
\(\det A=|A|=-3 \)
$$余因子A_{3,2}=|A|・(-1)^{3+2}=-3・(-1)^{5}=3$$
余因子展開の意味と手順
さて、少し複雑でしたが余因子を求めることが出来ました。
ここからは、その余因子が実際にどのように役に立つのか『余因子展開』という応用例を紹介します。
余因子展開の手順と行列式を求める方法
まずは、以下のイラストをご覧ください。
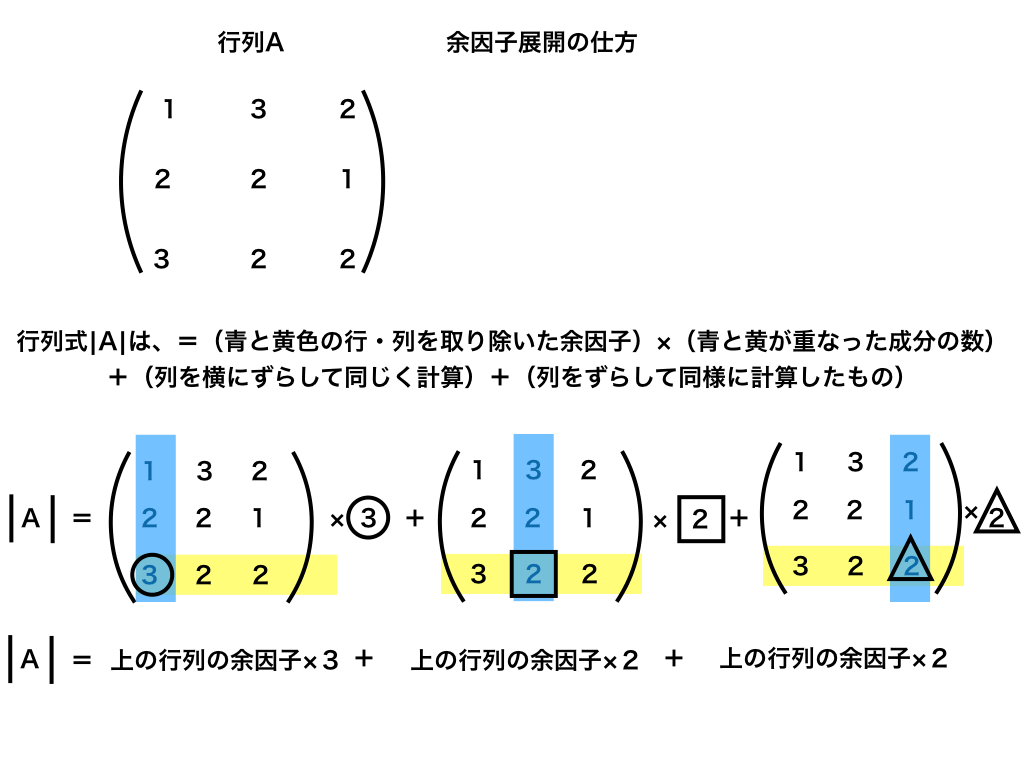
このイラストを基に、余因子展開のやり方と行列式の求め方を1つ1つ解説していきます。
今、$$A=\begin{pmatrix}
1 & 3 & 2 \\
2 & 2 & 1 \\
3 & 2 & 2
\end{pmatrix}$$の行列式を求めたいとします。
3×3行列なので、サラスの公式を用いても良いのですが、余因子展開の仕方を知っておくと4×4行列などサイズが大きくなっても(計算量は増えますが)公式に頼らずに行列式を求めることが出来ます。
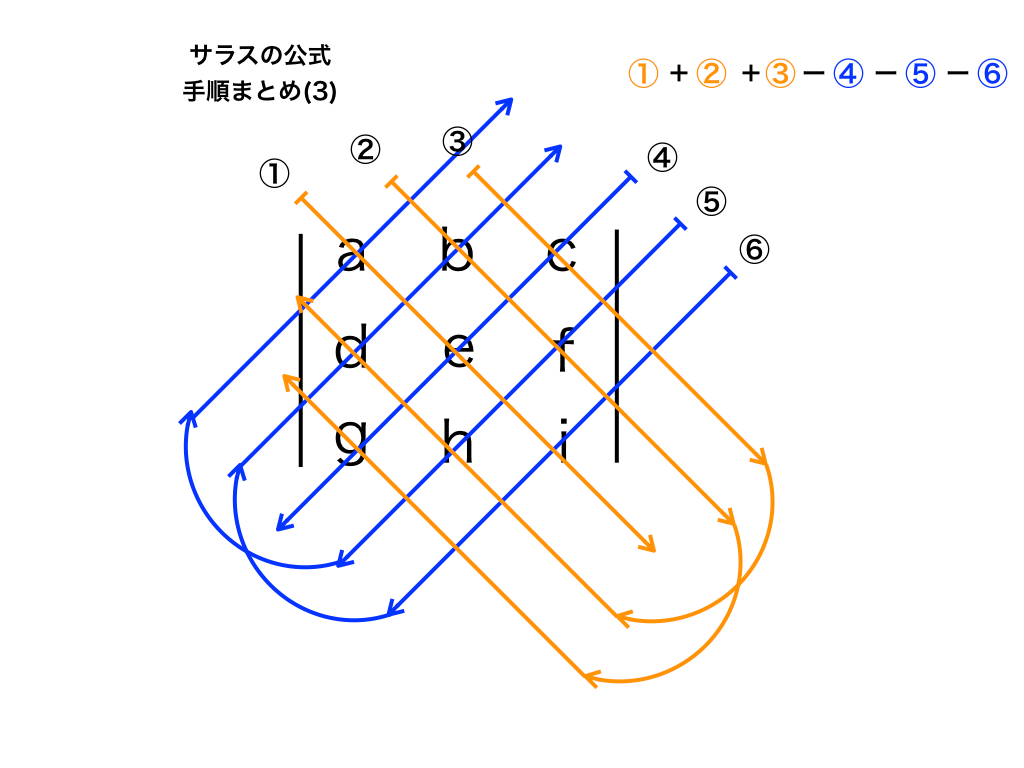
<参考:サラスの公式>
手順その1:任意の行を決めて1列目の余因子を作る
まずは、どの行でも良いので1つ行を決めます。(今回は3行目)。そして、一番左の1列目を同時にとって、\(余因子A_{3,1}\)を作ります。
手順その2:同じ行の2列目の余因子を作る
次に、列を1つ横に動かして\(余因子A_{3,2}\)を同様に作ります。
手順その3;同様に3列目の余因子を作る
このようにして、一つ一つ3列目(右端)まで余因子を求めていきます。\(A_{3,3}\)
手順4:1〜3で取り去った行と列が重なっている部分を調べる
※この4と5が余因子展開で最重要の部分です。もう一度余因子展開の図を再掲すると、

\(A_{3,1}\)を求めた時の成分\(a_{3,1}=3\)(イラストでは丸で囲っている部分)
\(A_{3,1}\)を求めた時の成分\(a_{3,2}=2\)(四角で囲っている部分)
\(A_{3,1}\)を求めた時の成分\(a_{3,3}=2\)(三角で囲っている部分)
手順5:手順4で求めた3つの数の和が元の行列A の行列式
手順1〜3で求めた余因子と手順4で調べた成分を次のようにかけて足し合わせたものが元々の行列Aの行列式と等しくなります。
\(\det A=A_{3,1}a_{3,1}+A_{3,2}a_{3,2}+A_{3,3}a_{3,3}\)
上の式が正しいかどうか、実際に計算してサラスの公式と一致するかチェックしてみましょう。
まず\(A_{3,1}=(3-4)×(-1)^{4},\)
\(A_{3,2}=(1-4)×(-1)^{5},\)
\(A_{3,3}=(2-6)×(-1)^{6}\)
これらを上の式に代入すると、\(\det A=|A|=-1×3+3×2+(-4)×2=-5\)
サラスの公式では、\(\det A=|A|=4+9+8-12-2-12=-5\)
と確かにどちらも行列式=−5//と一致しました。
余因子展開を使う場面
実は、この(余因子展開の)式が威力を発揮するのは、サラスの公式が使えない場合と成分に『0』が含まれている場合です。
これらの場合については、「現在制作中の演習問題編」で紹介します。
次回:余因子行列と逆行列の作り方(3)へ
次回:線形代数(11)では、余因子行列という《行列の各成分が余因子》の行列の作り方・注意点、さらにその余因子行列を応用して『逆行列』を作る方法を紹介します。
(逆行列の残り2つの求め方:2×2サイズでの公式と、『掃き出し法の利用』)については、
→「逆行列の意味と求め方2選(線形代数3)」をご覧ください。
線形代数(入門)シリーズと行列式の計算量を減らすコツ(NEW)
<NEW!>・「余因子行列の求め方とその利用法(逆行列の求め方)」
最後までご覧いただきありがとうございました。
ご意見や、記事のリクエストがございましたらぜひコメント欄にお寄せください。
・B!いいね!やシェア、Twitterのフォローをしていただけると励みになります。
・お問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。

