
行列式の性質・計算(線形代数12)
<今回の内容>:特に4×4などの大きなサイズの行列式を計算するときに役立つ性質と、習得するための演習問題をまとめました。
<予備知識>:必要に応じて→「線形代数の解説記事まとめ」をご覧ください。
行列式の性質と計算への応用
行列式を計算する際に、3×3くらいのサイズの行列位までならば、なんとかサラスの公式で解けます。
が、それ以上のサイズであったり、3×3のサイズでも素早く計算したい時に、以下で紹介する性質を知っておく必要があります。
行列式の性質を使って目指すカタチ
とにかく、「0」の成分が任意の行/列に並ぶ状態を目指します。
$$例:\begin{vmatrix}
1 & 2 & 1 & 3 \\
0 & 3 & 2 & 1 \\
0 & 1 & 2 & 2 \\
0 & 4 & 1 & 5
\end{vmatrix}のような形を目指します。$$
その理由は以前解説した【余因子展開】<参考:「余因子と余因子展開を利用して行列式を求める方法」>の計算量を大幅に減らせるからです。
行の基本操作と行列式の値に与える影響
まずは「行」を操作するときに行列式の値がどのように変化するかを見ていきます。
・ある行と別の行を入れ替える
行を別の行と入れ替えたとき、行列式の値の符号がー(マイナス)倍されます。
・任意の行だけスカラー倍(2倍、6倍など)する
n行のうちの1行だけでもスカラー倍すると、行列式の値もそのスカラー倍されます。
・スカラー倍した行を別の行と足し引きする
例えば3行目をm倍して4行目に加える、といった操作をしても行列式の値は変わりません!
列の基本操作と行列式の値
次に、列の操作と影響です。実はある行列の行列式とその行列の転置行列の行列式は同じことから、『行での操作による行列式の値の変化』と『列の操作による変化』は同じになります。
・ある列と別の列を入れ替える
”列”を別の”列”と入れ替えたとき、行列式の値の符号がー1倍されます。
・任意の列だけスカラー倍する
n”列”のうちの1”列”だけでもスカラー倍すると、行列式の値もそのスカラー倍されます。
・スカラー倍した列と別の列を足し/引きする
例えば2"列"目をm倍して3"列"目に加える、といった操作をしても行列式の値は変わりません。
行列式の定義式(このような性質が成り立つ理由)
このように便利な性質ですが、なぜ成り立つのでしょうか?
これらは、すべて”行列式の定義式”から証明できるのです。
(この部分は『置換』や『互換』・『sgn』などの解説が必要なので随時追加していきます)
定義式:$$\left| A\right| =\sum _{\sigma \in S_{n}}( sgn\left( \sigma \right) \prod ^{n}_{i=1}a_{(i,\sigma _{i})})$$
追記:「置換と互換、行列式の定義式を理解する」(←この記事で行列式の定義式の意味と、それを理解するための『置換』・『互換』・『sgn』などの解説を行なっています。)
行・列の基本操作の効果を実感してみる(演習編)
まずは3×3サイズの行列から今回学習した方法を問題を解きながら習得します。
3×3サイズ行列の演習問題
問1:以下の行列Aの行列式を求めよ。
$$\begin{pmatrix}
1 & 2 & 1 \\
2 & 5 & 1 \\
3 & 1 & 2
\end{pmatrix}$$
解答1
まず、余因子展開しやすいように1行1列の成分”1”以外の1列目の成分を0にすることを目標とします。そのためには、行に関する性質(操作)3より、
・(2行目ー1行目×2)と
・(3行目ー1行目×3)を行います。
$$\begin{vmatrix}
1 & 2 & 1 \\
0 & 1 & -1 \\
0 & -5 & -1
\end{vmatrix}$$
すると上のような形になります。
かなり簡単な行列式になったのでここでサラスの公式を用いても良いですが、余因子展開をもう一度だけしてみましょう。
$$1×(-1)^{2}×\begin{vmatrix}
1 & -1 \\
-5 & -1
\end{vmatrix}+$$
$$0×\begin{vmatrix}
2 & 1 \\
-5 & -4
\end{vmatrix}+0×\begin{vmatrix}
2 & 1 \\
1 & -1
\end{vmatrix}$$
このように、1列目2行・3行の成分を0にしたおかげで、実質的に計算するのは(1行1列目の成分)と|2行2列〜4行4列|の行列式のかけ算一回ですみます。
よって、
$$|A|=1×(-1)^{1+1}×{(1)(-1)-(-1)(-5)}=-6$$
|A|=-6・・・(答)
4×4行列の演習問題
次に、サラスの公式が使えないサイズに応用してみましょう。
問2:次の4×4行列Aの行列式の値を求めよ。
$$\begin{pmatrix}
1 & 2 & 2 & 3 \\
2 & 6 & 2 & 2 \\
2 & 1 & 3 & 5 \\
3 & 2 & 1 & 1
\end{pmatrix}$$
解答2
まず、2行目が全て2の倍数になっているので、2でくくります。(行に関する性質2より、まえに2が出て行列式の値に2倍する形になります。)
$$2・\begin{vmatrix}
1 & 2 & 2 & 3 \\
1 & 3 & 1 & 1 \\
2 & 1 & 3 & 5 \\
3 & 2 & 1 & 1
\end{vmatrix}$$
次に、1列目の第1行の成分以外を0にするために、
・『2行目ー1行目』
・『3行目ー2×1行目』
・『4行目ー3×1行目』
の操作を同時に行います。(初めは1つずつ操作しても構いません)
行に関する性質3より、『ある行をスカラー倍して、別の行と足し引きしても行列式の値は不変』です。
$$2・\begin{vmatrix}
1 & 2 & 2 & 3 \\
0 & 1 & -1 & -2 \\
0 & -3 & -1 & -1 \\
0 & -4 & -5 & -8
\end{vmatrix}$$
今度は、1列目の各成分で余因子展開します。1列2行・1列3行・1列4行の成分はすでに0にしてある為、計算するのは以下の(1行1列)×|2行2列〜4行4列|のみですみます。
$$2×1×(-1)^{1+1}×\begin{vmatrix}
1 & -1 & -2 \\
-3 & -1 & -1 \\
-4 & -5 & -8
\end{vmatrix}$$
この3行3列の行列式の1列目を、先ほどと同様に1行目の成分以外は全て0にします。(行に関する性質3より)
・1行目×3+2行目
・1行目×4+3行目
$$2×\begin{vmatrix}
1 & -1 & -2 \\
0 & -4 & -7 \\
0 & -9 & -16
\end{vmatrix}$$
先ほどと同様に、ここでサラスの公式を用いても良いです。
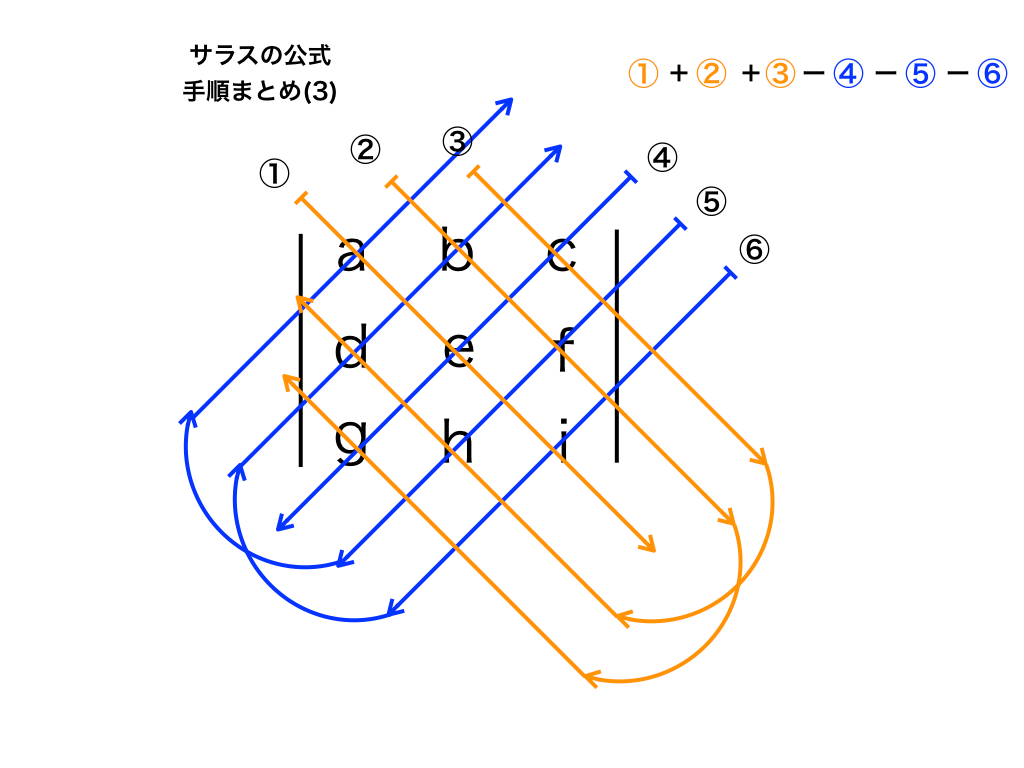
<サラスの公式(方法)再掲>
今回はもう一度余因子展開を行って次数を下げます。
$$2×1×(-1)^{1+1}×\begin{vmatrix}
-4 & -7 \\
-9 & -16
\end{vmatrix}$$
ここまでくれば、2×2の行列式を計算して2をかけるだけで問題2の行列式が求まります。
$$2×1×(-1)^{1+1}{(-4)(-16)-(-7)(-9)}$$
$$=2×(64-63)$$
よって、|A|=2・・・(答)
行列式と面積・体積との関係
行列式には、これまで説明してきた性質・特徴以外にも様々な興味深い意味があります。
ここではその中から、行列式と座標上の図形の関係について簡単に紹介します。
平行四辺形の面積と行列式の値が一致する!
具体的な例を挙げます。
今列ベクトル$$\vec{u}=\begin{bmatrix}
5 \\
3
\end{bmatrix}と,\vec{v}=\begin{bmatrix}
-1 \\
2
\end{bmatrix}$$があるとき、2つのベクトルを$$行列A=\begin{pmatrix}
5 & -1 \\
3 & 2
\end{pmatrix}$$
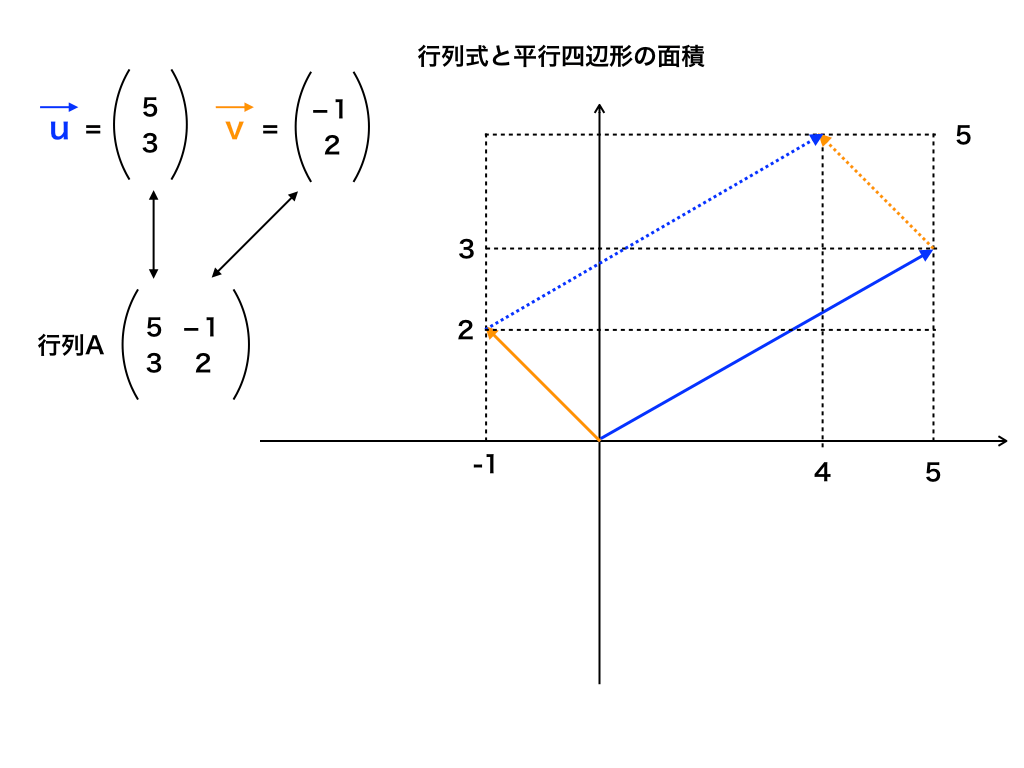
に並べます。そして、”ベクトルu”と”ベクトルv”によってできる平行四辺形(以下の図参照)の面積は、行列式:|A|と等しくなるのです!
実際に計算してみましょう。
$$\det A=|A|=(5)(2)-(-1)(3)=13$$よって、行列式は『13』と求まりました。
一方、青のuベクトルとオレンジのvベクトルによる平行四辺形の面積は、まず(全体の四角形)から(面積が等しい2組の3角形の面積)を引くことで求めることが出来ます。
5×{5-(-1)}=30
大きい方の三角形の面積は:5×3×1/2
小さい方の面積は:2×1×1/2
したがって、30-(5×3×1/2×2)-(2×1×1/2×2)=13
と確かに一致しています。
もちろんこれは偶然ではなく、ベクトルの成分表示による計算と、座標上で等積変形を利用することできちんと証明することが出来ます。(ぜひチャレンジしてみて下さい)
3次の行列式は平行6面体の体積と一致する
また、ここでは計算しませんが、3×3の行列式の値は『平行六面体の体積』と一致し、これも平行四辺形の面積の証明と同様の手順で(一部、余因子展開:「余因子と余因子展開とは?」を利用しますが)証明できます。
まとめと線形代数の関連記事
・余因子展開しやすい形を目指す(0が並ぶ形)
・行・列とも同様の操作を行う事ができ、行列式の値への影響も同じ
・行列式と面積・体積との関係
・この他にも、様々な性質があるので随時更新していきます。
必見!行列の記事
以下の記事では、高校数学のベクトルの基礎から行列・1次変換などなど大学の線形代数の基本まで解説した記事をまとめています。
>>「【随時更新】0からわかる!線形代数の入門シリーズ総まとめ」ブックマーク推奨です!<<
最後までご覧いただきまして有難うございました。
スマナビング!では、読者の皆さんのご意見や、ご質問、記事のリクエストなど募集しています。ぜひコメント欄までお寄せください。
いいね!やB!、シェア、をしていただけると励みになります。
・その他のお問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。

