
部分積分の仕方と迷わず計算する為のコツを紹介!
<この記事の内容>:「積分法の基本公式(1)」に引き続き、今回は「部分積分の仕方」を紹介していきます。
タイトルの通り、部分積分を楽に解くコツ(下メモ法)を解説しているので、以下の様な人は必見です!
<この記事を読むべき人>
・部分積分の公式がややこしくて苦手→1歩1歩手順を図解しているので、文字だけではわかりにくかった式もよく理解できます
・2つの関数のうちどちらを微分/積分の形にすれば良いかわからなくなる。
目次(タップした所へ飛びます)
部分積分とは
数学3の積分では、単なる公式だけでは解決できないパターンも沢山あります。
そのため色々な計算法があるのですが、今回はその中でも「部分積分」を紹介していきます。
部分積分の公式
具体的な式は以下の通りです。一つ目の定義式において、微分の記号である「’」の位置に注意しましょう。 $$\int f'(x) g(x) dx=f(x) g(x) -\int f(x) g'(x) dx$$
ただし、これだけだとややこしく感じるので、実際に具体的な問題を使って解説していきます。
次の不定積分を計算せよ。
\(\int xe^{x}dx\)
部分積分する手順とコツ【下メモ法】
ここから、実際に部分積分していきます。見通しをよくするため、下にメモ(のようなもの)と「箱」を書きながら積分します(下メモ法:勝手に名付けたので良い名前があれば教えてください・・・)。
なるべくわかりやすいように、手順を図解していきます。
1:微分する関数を選ぶコツ
手順1:まずはじめに、「x」と「ex」のどちらを微分すると楽(単純)な関数になるかを考えて選びます。ここでは当然「x」です。

2:もう一方の関数を積分する
手順2:(1)で選んだ簡単な方の関数を微分して、その下に書きます。同時に、もう一方(ここではex)を積分した結果も書き込みます。(exは積分してもex,ここでは積分定数Cは書きません)。

3:矢印の向きに注意して書き込む
手順3;以下の図のように、微分した関数は下向きに矢印を・積分した関数は下から上向きの矢印を書き込みます。
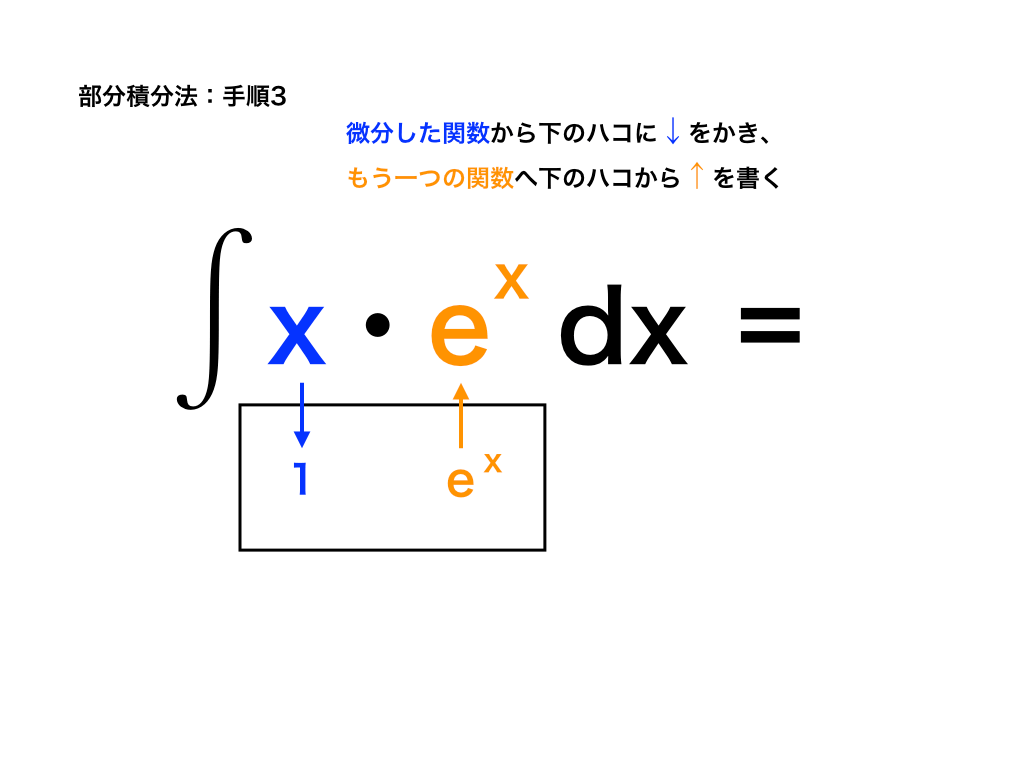
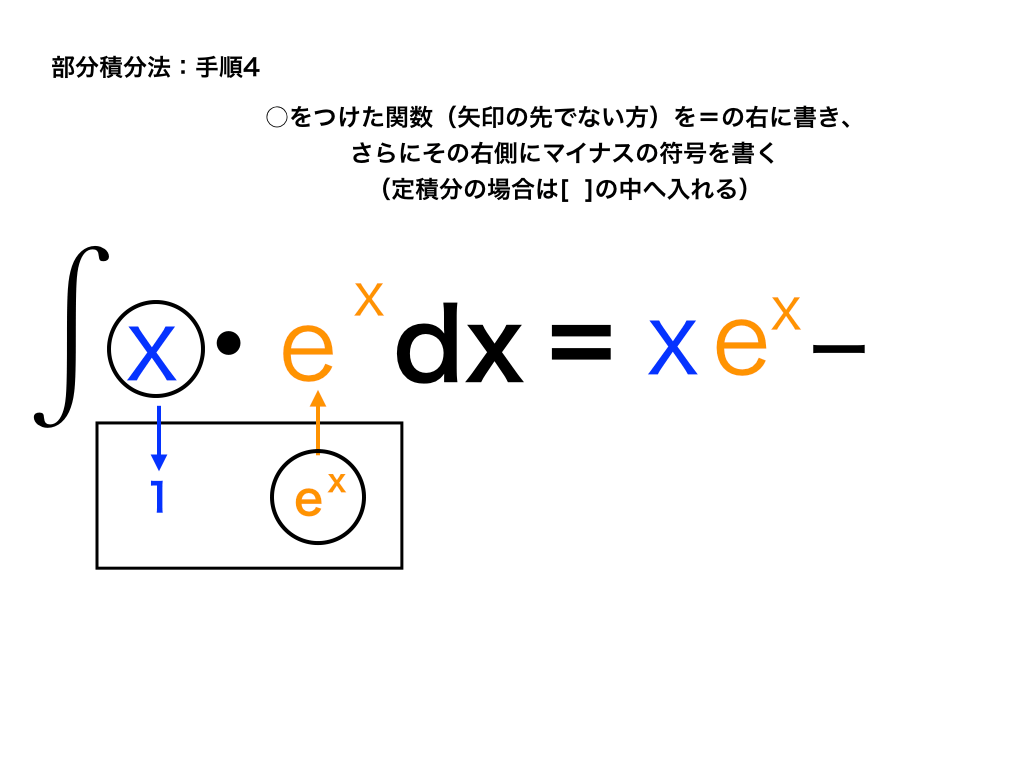
4:丸で囲った2つの関数を=の右に書く
手順4:矢印の先でない方(以下の図中では「x」と「ex(積分した方です)」)をそのまま=の右側に書きます。
※不定積分の場合です。定積分のときは[]で囲んで計算します。
5:メモした箱の中の∫2関数dxを後ろにおく
手順5:元の∫xexdxの下に書いた”ハコ”の関数を手順4で書いた関数の右側に書き∫1×ex dxとします。
 ここで、\(\int e^{x}dx=e^{x}+C (Cは積分定数)\)
ここで、\(\int e^{x}dx=e^{x}+C (Cは積分定数)\)
より、結果的に$$\int xe^{x}dx=xe^{x}-e^{x}+C$$
と積分することができました。
\(\log{x}\)を部分積分してみる(工夫と実践)
手順はある程度理解できたでしょうか?この項では、先ほどの”下メモ法のコツ”を意識して、
\(\log{x}\)の積分を求めてみましょう。
\(\log{x}\)の積分は公式として載っているかと思いますが、自分で導けるようにしておきましょう。
\(\log{x}\)の部分積分の問題点と工夫
さて、実際にlogxを部分積分をしようとすると、関数が1つしかないことにすぐ気付くかと思います。
これでは、上で解説した下メモ法が使えない・・・
その為、なんとか関数を2つにする方法を考えます。
すると、"logx=1×logx"にすれば全て解決することがわかります。(1をかけても被積分関数はlogxのままです)
logxの部分積分の手順1
logxを1×logxとみなして、1とlogxのどちらを微分すれば簡単な関数になるかを考えます。
(1)'=0と(logx)'=1/xを見比べると、一見(1)の方を微分したくなりますが、
そうなると手順3で紹介した(logx)の積分を知っている必要が出てきます。
・・・今logxの積分をしているのに、その答えを知っているはずがありません!
そもそも知っていれば、部分積分などしなくて良いのです。
そこで(logx)の方を微分することにし、1の積分=xと、(logx)'=1/x を”下メモ”しておきます。
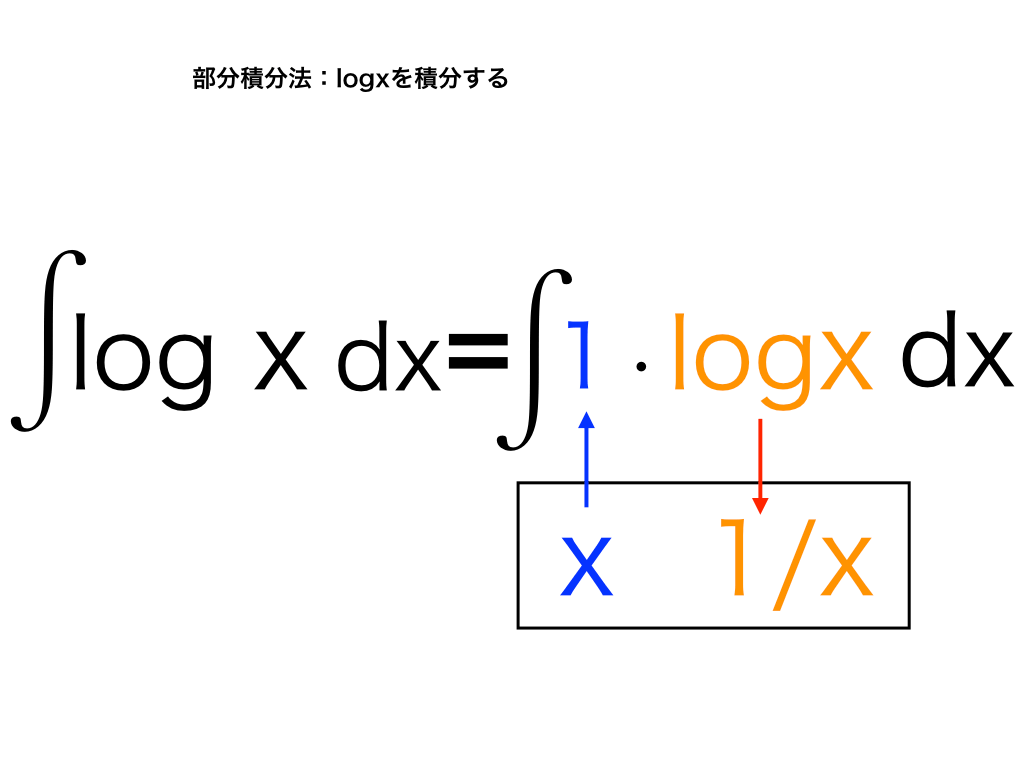
logxの積分の手順2
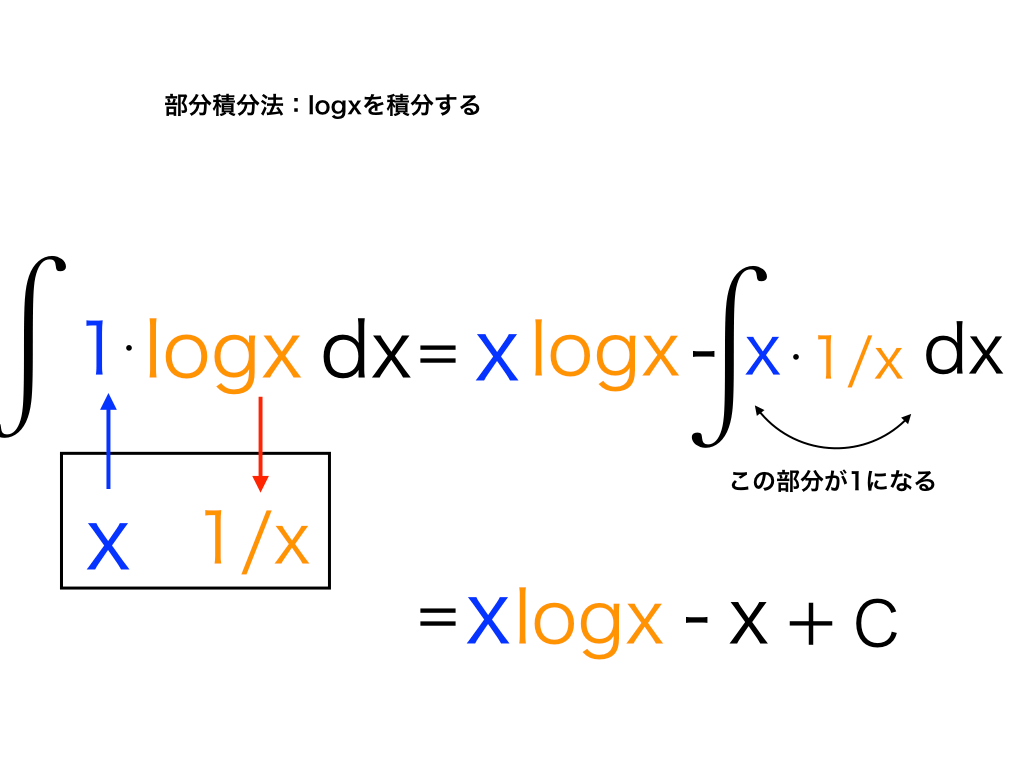
これまで同様に、下にメモしておくと”ハコ”のなかみが『x・1/x』となっていますね。
つまり右辺にxlogxーと書いた後に計算する、∫x・1/x dx=∫1dxとなり大変簡単に積分できます。
あとは、以下の図の通り計算していくと、
\(\begin{aligned}\int 1× \log {x} dx=x\log x-\int x\cdot \frac {1}{x}dx\\
=x\log x-\int 1dx\\
=x\log x-x\end{aligned}\)
となって、教科書などにも載っている「自然対数logxの積分=xlogx-x+C ;Cは積分定数)が導けます。
このように、\(稀に\int f(x) dx=\int 1× f(x) dx\)
とする事で上手く計算できる事があります。
部分積分法で色々解いてみよう
ここから、実際に手を動かして、例題を解きながら部分積分の仕方を身につけます。(解説を見る前に、一度自分で解いてみてください)
(例1):2回積分を行う(三角関数)タイプ
\(\int x^{2} \sin x dx\)
(例2):自然対数が入ったタイプ
(例題2):次の部分積分を計算せよ。\(\int x\log{x} dx\)
(解説1):繰り返し部分積分
微分して簡単になるのはx2の方です。したがって、手順1の青の関数=x2、オレンジの関数=sinxとして、部分積分を進めていきます。
∫sinxdx=-cosx (積分定数は省略)ただし計算を進めるとわかりますが、一回では積分が完了せず、もう一度部分積分する必要があります。
<解答1>
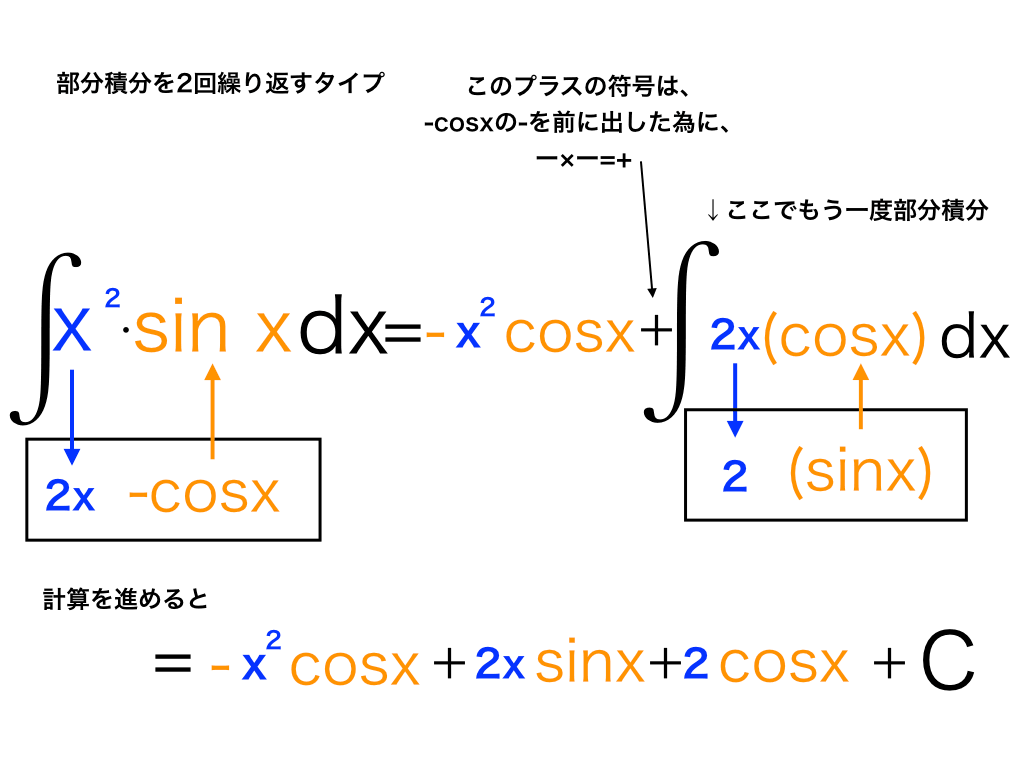 上の図のように、∫2x・cosx dxを再び部分積分して、式を整理すると、
上の図のように、∫2x・cosx dxを再び部分積分して、式を整理すると、
=ーx2cosx+2xsinx+2cosx+C (Cは積分定数)・・・(答)
解説2:対数関数の積分
例題1よりもこちらの方が簡単かもしれません。logxがある時点で、これを微分するほうの関数と決定できます。あとはもう一方の関数xの積分を下にメモしておきます。(∫xdx=x2/2)。
<解答2>
$$\int x\log{x} dx=\frac{x^{2}}{2} \log{x} -\int \frac{x^{2}}{2}× \frac{1}{x} dx$$
積分の部分のxが打ち消しあってxが残るので、
$$\frac{x^{2}\log{x}}{2}-\frac{1}{2}\int x dx$$
$$=\frac{x^{2}\log{x}}{2}-\frac{x^{2}}{4}+C$$
部分積分まとめ
さて、部分積分法にも少しは慣れてきたでしょうか?数学3、特に積分は計算の正確さと速度が重要になってくるので、類題を探して沢山の問題を解いていきましょう。
・積分する際に、”logx”があれば部分積分を考える
・∫(関数)・(関数)dx のカタチの積分では、微分して簡単になるものがないか探す
・今回学習した“部分積分”を応用した問題に”積分漸化式”があります。
次回は積分漸化式【作成済み】の具体的な問題を解説していきます。
数学Ⅲ:微積分の記事一覧へ
次回予告:(積分漸化式と微積まとめ)
「【作成済み】積分漸化式の4パターンとその解き方」
>>「数Ⅲで学ぶ微分・積分法とその応用の記事まとめ」<<
最後までご覧いただきまして有難うございました。
当サイト「スマナビング!」では皆さんのご意見や、記事のリクエスト、質問・ご意見をお待ちしています。ぜひコメント欄にお寄せください。
snsでいいね!やシェア、B!、公式Twitterのフォローをしていただけると助かります。
・その他のお問い合わせ/ご依頼は、お問い合わせページよりお願い致します。

