三角比の表と面積公式・正弦定理/余弦定理を一記事で解説 !

【保存版】三角比の基礎知識から公式まとめ【完全網羅】

＜この記事の内容＞：数学１で習う三角比の基礎の基礎（サイン・コサイン・タンジェントが三角形のどの辺の比なのか？）というレベルから、

・三角比の表、重要な（正弦・余弦定理）や面積公式・その応用問題などについて豊富にイラストを使用して解説しています。

三角比とは何か？

三角比とは、直角三角形の３辺の間に成立する”比”のことを言います。

具体的には、sin（サイン：正弦）、cos（コサイン：余弦）、tan（タンジェント：正接）の３つの比を学習します。

（他にも、cot（コタンジェント）、sec（セカント）、csc（コセカント）などがありますが、高校数学の範囲では、基本的に上の三つを知っていれば問題ありません。）

sin/cos/tanは３辺の"どこ"と"どこ"の比なのか

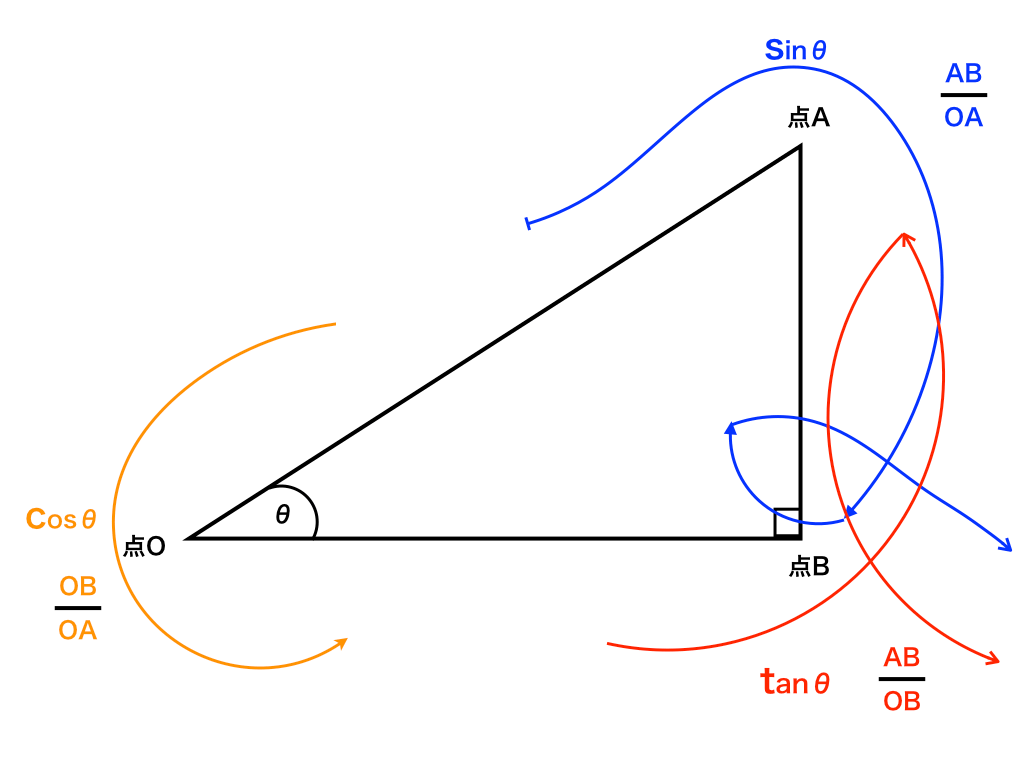
まず、これから扱う三角形（頂点をO、A、Bとし、角ABOが直角、∠AOB＝θとします）のθを、

以下の図のように配置します。（θと直角の位置に注意してください）

＜sin・cos・tanの解説図＞

sinθは、（青字の部分）英語の筆記体で小文字のsを書くときのように、辺OA分のAB

cosθ（図中のオレンジの部分）は、同様に小文字のcを書くようにして、辺OA分のOB

tanθは、（赤字の部分）これも同じくtを書くように、辺OB分の辺ABの比がそれぞれの値になります。

三角比の表

はじめに三角比を勉強するときに、三角比の表を作るかもしれません。

慣れてくると、表などを見なくてもすぐ数値を思い出せるのですが、それまでは以下の表を参考にしてください。

なお、下の項で紹介する、sin(90°±θ)などの変換を使ったり、$$tanθ=\frac {\sinθ}{\cosθ}$$

（三角比・三角関数の相互関係より）を利用すると、記憶量をかなり減らすことができます。

うまく組み合わせてください！

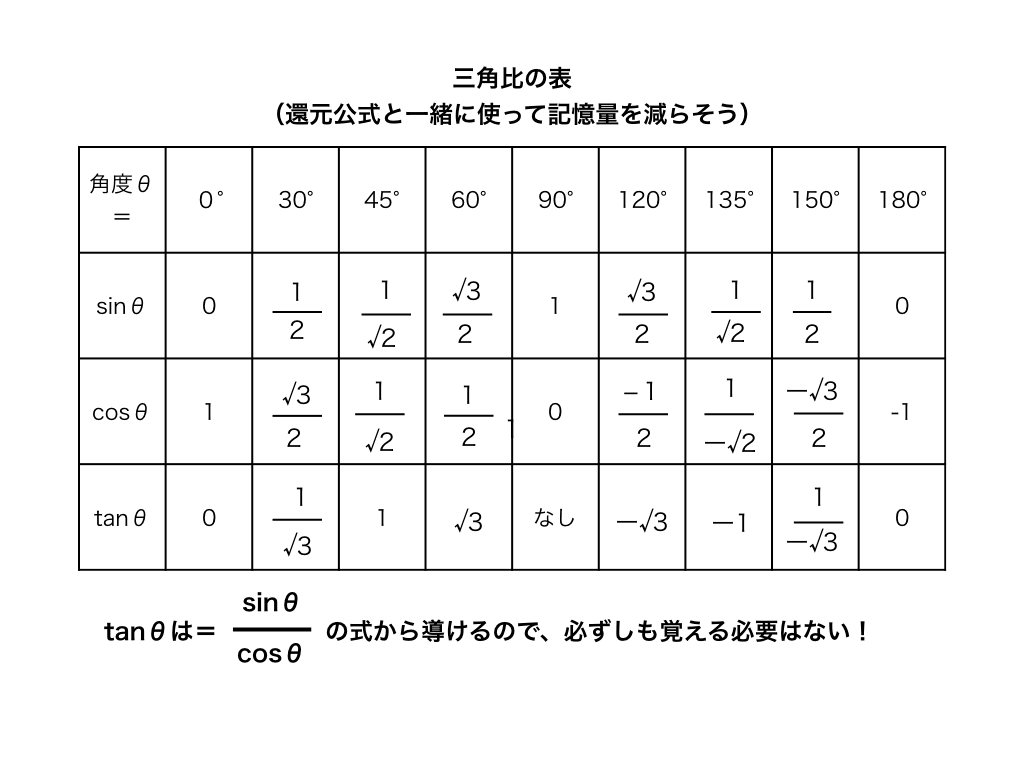
＜三角比の表＞

tan90°の値がない理由

tanθ=sinθ/cosθより、θ＝90°のときは分母のcos90°＝０となり、０で割ることができないためです。

sin(90°±θ）やcos(180°±θ）などの変換が苦手な人へ

見出しにあるように、サインθやコサインθに９０°を足したり、180°を引いたり、といったタイプの問題を苦手とする人は非常に多いです。

これらは、「余角・負角・補角の公式（合わせて『還元公式』）」という名前がついているのですが、この公式を覚えることは非常に効率が悪いので（１８種類以上もあるのです。。）オススメしません。

代わりに、２stepでどのようなタイプの変換もできる方法を紹介しているので、

→「三角関数(比)の還元公式の問題を暗記せずに２stepで解く方法」をあわせてぜひご覧ください。

正弦定理と余弦定理

さて、三角比では様々な問題が出題されますが、必ずと言っていいほど使う定理（公式）が２つあります。

それが『正弦定理』と『余弦定理』です。ただし、この２つの定理だけでは簡単な問題しか解けません。

応用レベルの問題を解くには、図形の性質（数A)や中学校の幾何の知識が必要になることも多いです。三角比でつまったら、幾何を見直してみるといいでしょう。

正弦定理とは

これは、半径Rの円に内接する三角形の辺の長さと、反対側にある角の正弦（sin)の関係を式で結んだものです。

今、下の図のようになっているとき、２R＝a/sinA =b/sinB =c/sinC

が成り立ちます。

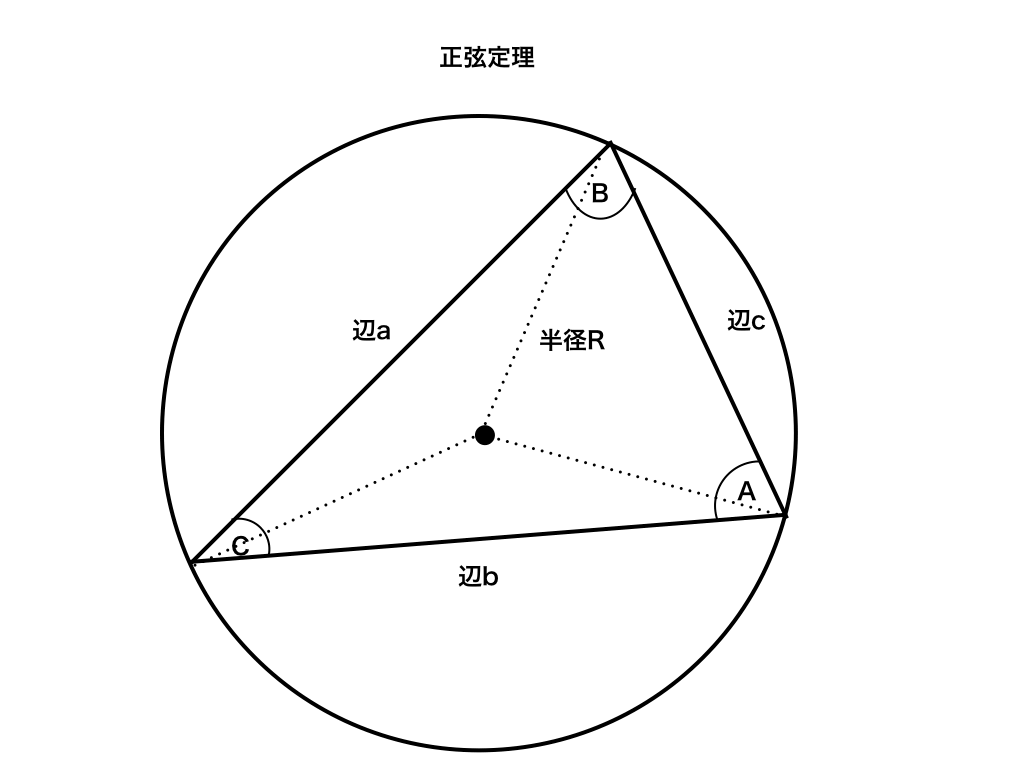
＜正弦定理の図＞

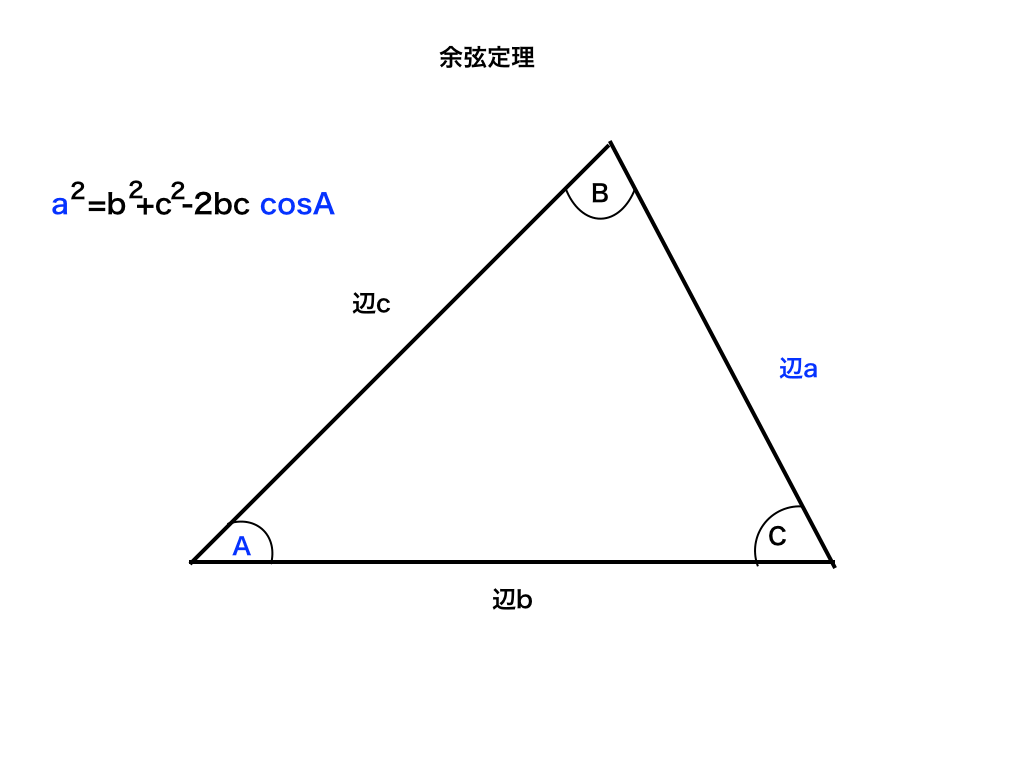
余弦定理とは

余弦定理は、「余弦」と名付けられているようにcosを使った定理です。

三角形の２辺の長さと対応する間（あいだ）の一つの角度がわかれば、その角の向こう側の辺の長さが求まる定理です。＜余弦定理の図参照＞

a²=b²+c²-2bc cosA ：辺aを求めるので、a以外のb,cの２乗ー2bc ×cosA (Aは辺b、cに挟まれた角度）

これと同様に、b²,c²の余弦定理も文字をそれぞれ入れ替えるだけで使えます。

従って３種類すべてを覚えておく必要はなく、どれか一つを覚えておいてその場で作るのが得策です。

一応残りの２つも書いておくと、

b²=a²+c²-2ac cosB

c²=a²+b²-2ab cosC

となります。

＜余弦定理の図＞

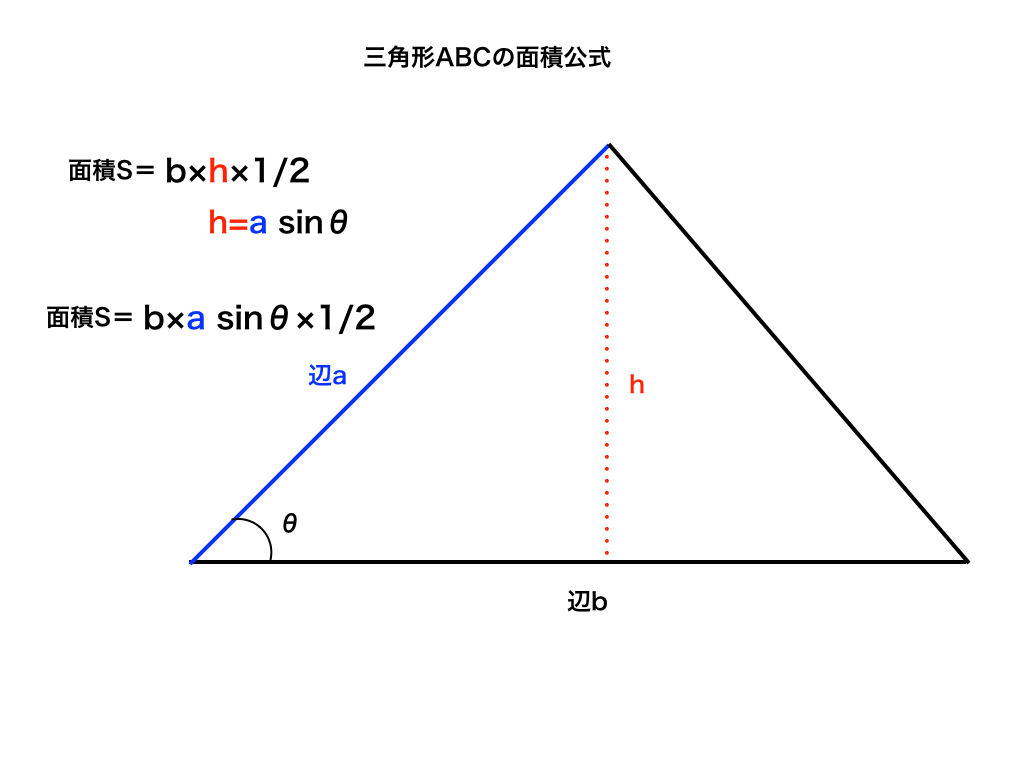
＋α：三角形の面積Sを求める公式(3)

正弦定理・余弦定理に＋αして知っておきたいのが、三角形の面積を求める公式です。

面積をSとして、S=absinθ/2

三角形の面積は『底辺×高さ×1/2』 で求まりますが、（これは小学校の算数ですね）

三角比の正弦（sin）を用いることで、”高さ”の部分を求めることができることを利用した公式です。

（図中のhを高さとして、三角形の面積はb×h×1/2,ここでhが未知数なのでaとθを使って、h＝asinθより、S=b×asinθ×1/2）

＜三角比を使った三角形の面積公式の図＞

定着用例題：円に内接する色々な三角形の面積を求めてみる

さて、ここまでの知識のまとめとして、円に内接する三角形の面積を求めてみましょう。

まず、円を８等分し、下図のように反時計回りにアルファベットを振っていきます。

そのうちの3点を選ぶことで面積の異なる三角形ができます。

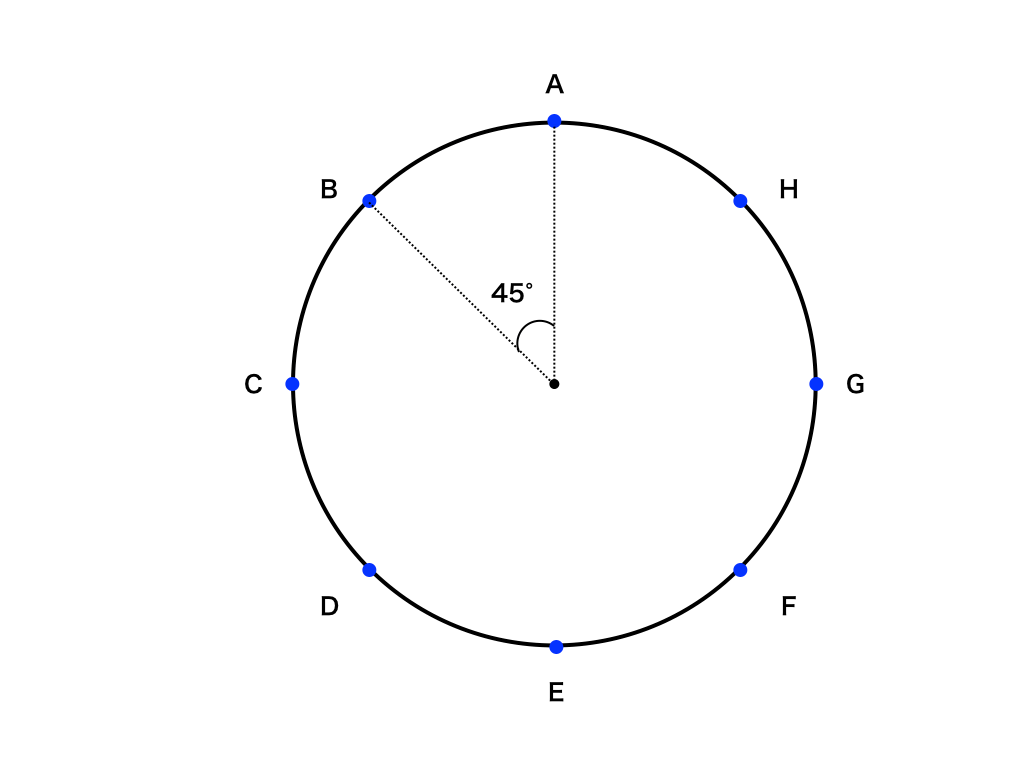
そのそれぞれの面積Sを正弦・余弦定理などを用いて求めてみましょう。

三角形ABCの面積

まず、円を８等分しているので中心の点をOとして、∠AOBなどの角度は360°÷8=45°になります。

ここで、ABの長さを”余弦定理”を用いて求めてみましょう。

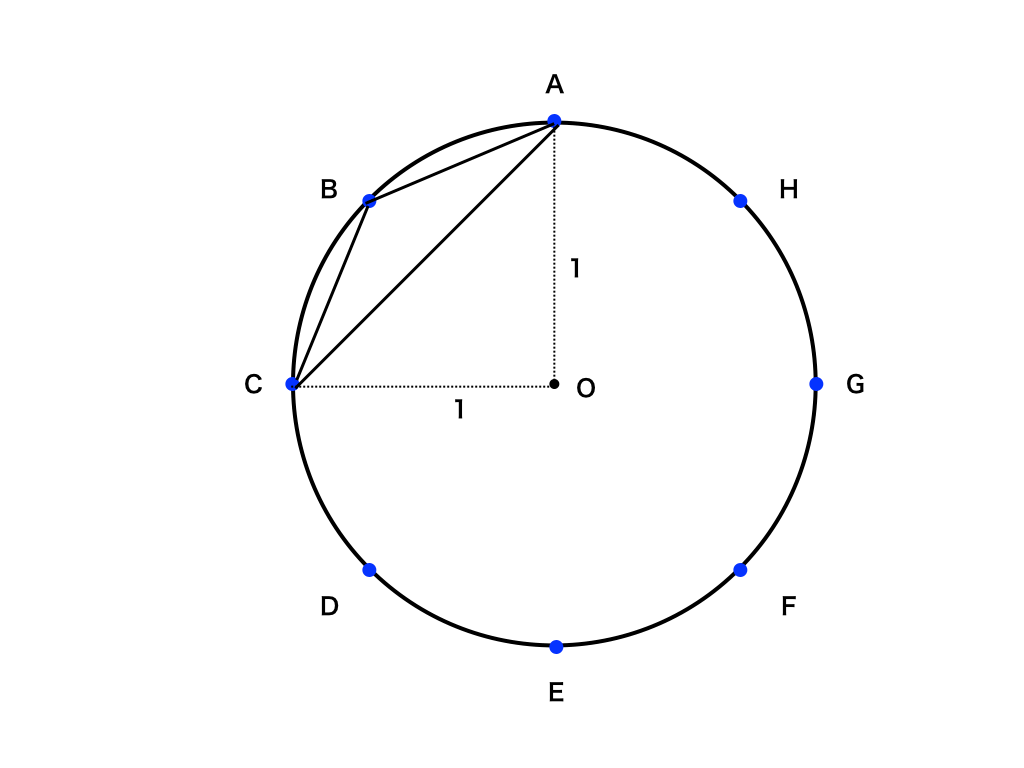
AB^２＝AO^２＋BO^２ー２（AO)(BO)cos 45°

より、$$AB^{2}＝1+1-2×\frac{1}{\sqrt {2}}$$

これを解いて、$$AB=\sqrt {2-\sqrt {2}}$$

ここで、ABCDEFGHが正八面体であることから、∠ABC=1080°÷8=135°

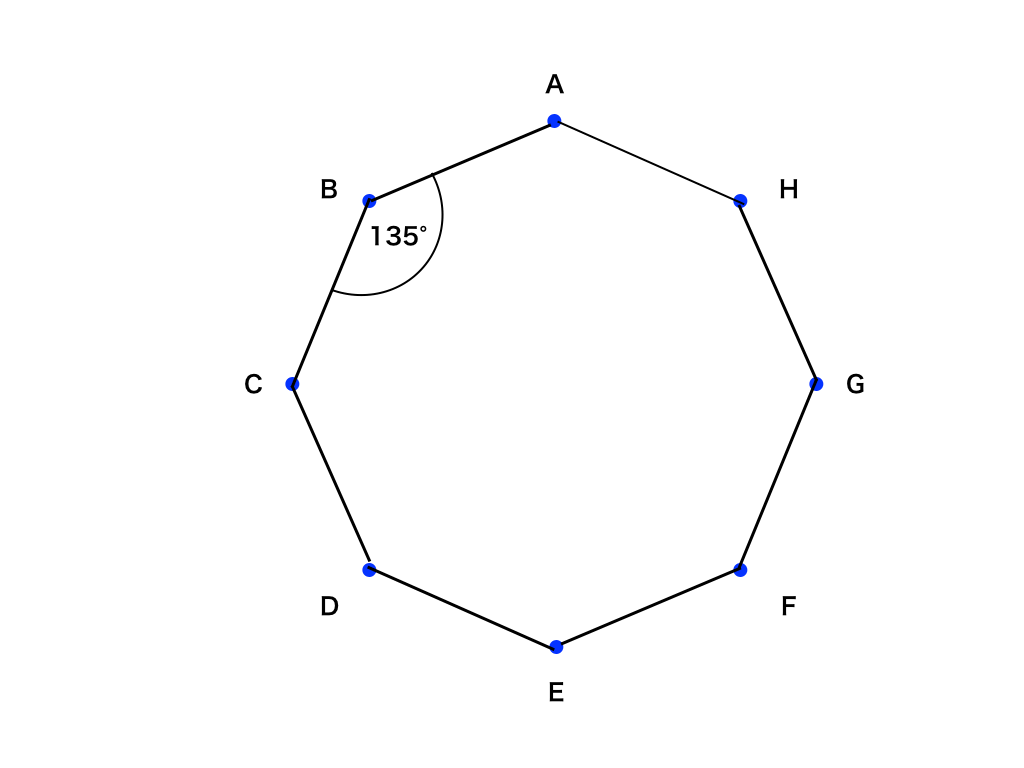
＜正八角形＞

三角形ABCを、上で紹介した『三角形の面積を求める公式』を使って

$$S_{ABC}=\frac {1}{2} × AB^{2}× sin135°$$より、

$$S_{ABC}=\frac {2-\sqrt {2}}{2} × \frac {\sqrt{2}}{2}=\frac {1+\sqrt {2}}{2}$$

三角形ABDの面積

∠DAH＝90°、∠BAH＝135°より、∠BAD=45°

ここで、$$AB=\sqrt{2-\sqrt {2}}とAD=\sqrt{2+\sqrt {2}}$$より、

AB×AD×1/2×sin45°＝1/2・・・（答）

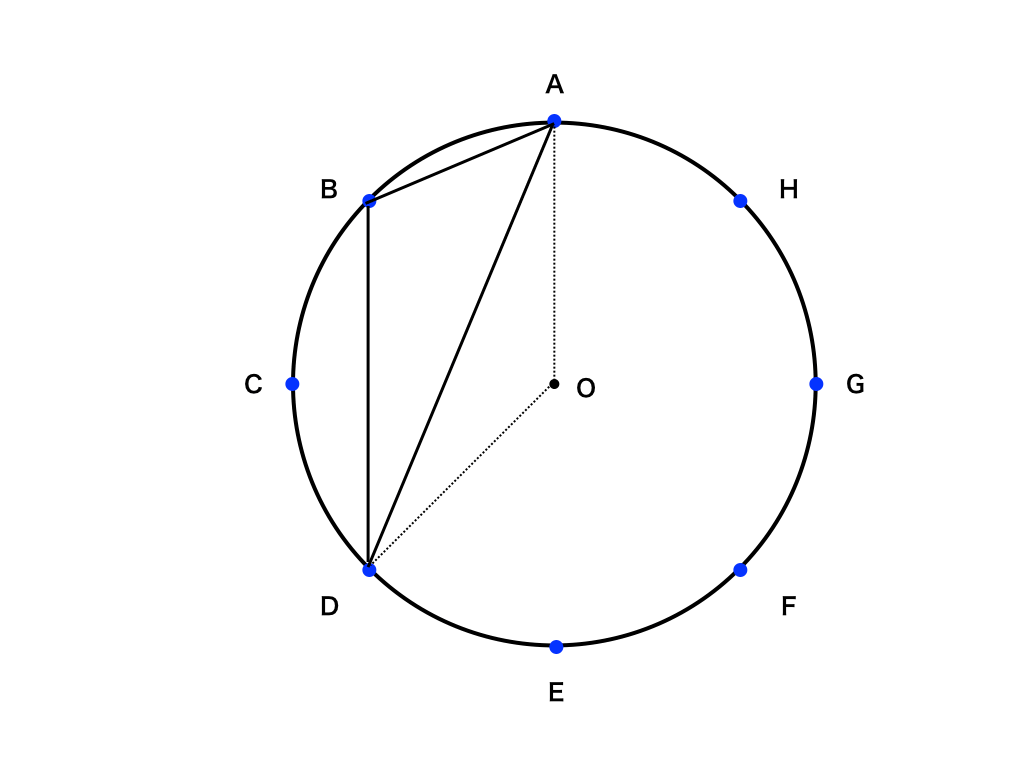
三角形ABEの面積

三角形ABEの面積は、∠ABE=90°（タレスの定理、円周角の定理より）であることから、

BE²+AB²=2²より、$$BE^{2}=4-(2-\sqrt {2}),BE=\sqrt {2+\sqrt {2}}$$

よって、BE×AB×1/2=$$\sqrt {2+\sqrt {2}}×\sqrt {2-\sqrt {2}}×1/2=\frac {\sqrt {2}}{2}$$

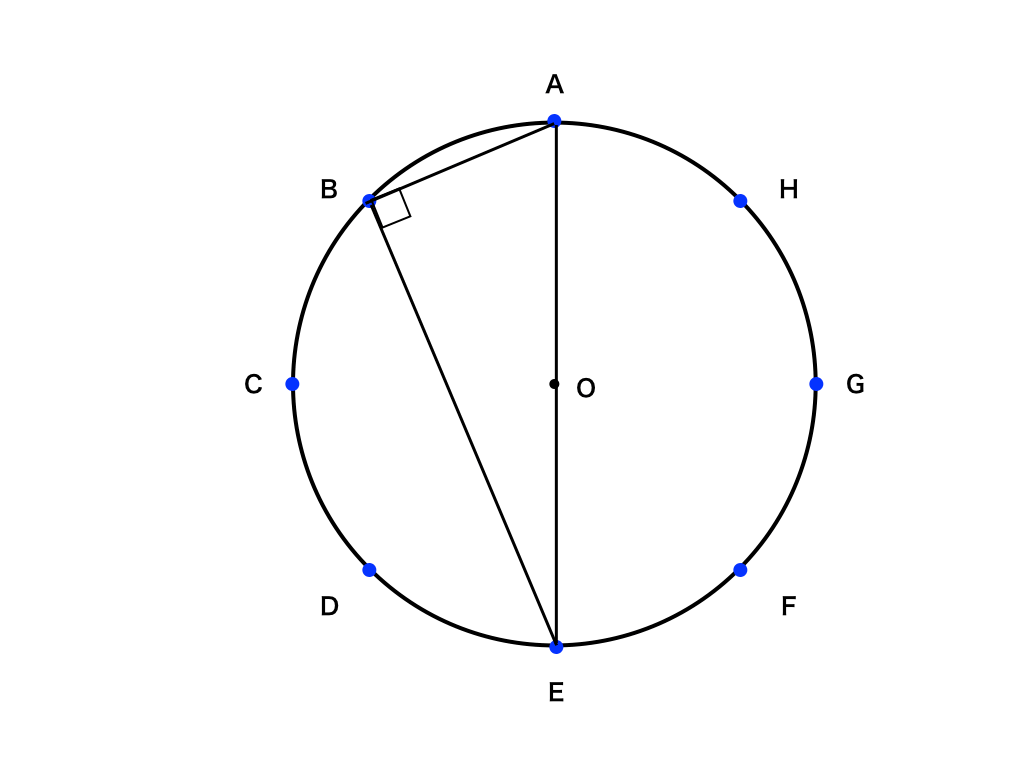
三角形ACEの面積

三角形ACEは、∠ACE=90°,AC=AE＝√２,より、√２×√２×1/2=1

よって面積は１です。

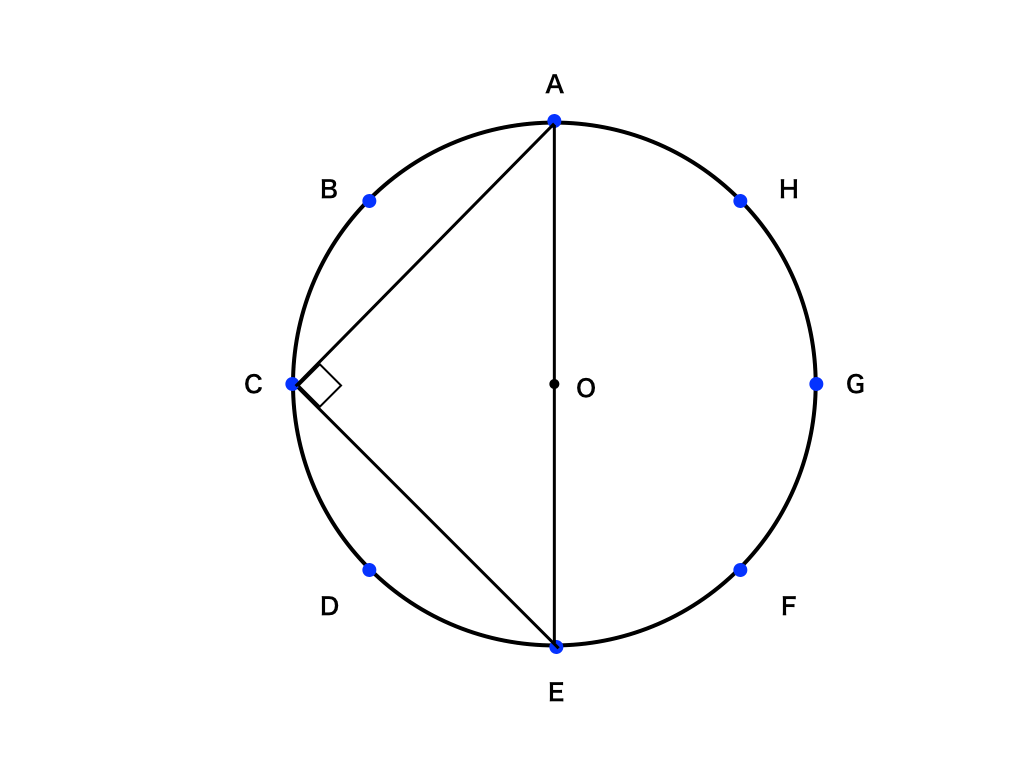
三角形ACFの面積

中心角∠AOCが90°であることから、円周角の定理より∠AFC=４５°。

$$BEが\sqrt {2+\sqrt {2}}だったので、AF=CF=\sqrt {2+\sqrt {2}}。$$

よって、三角形の面積公式（３）より、$$1/2×AF×CF×sin45°=\frac {1+\sqrt {2}}{2}$$

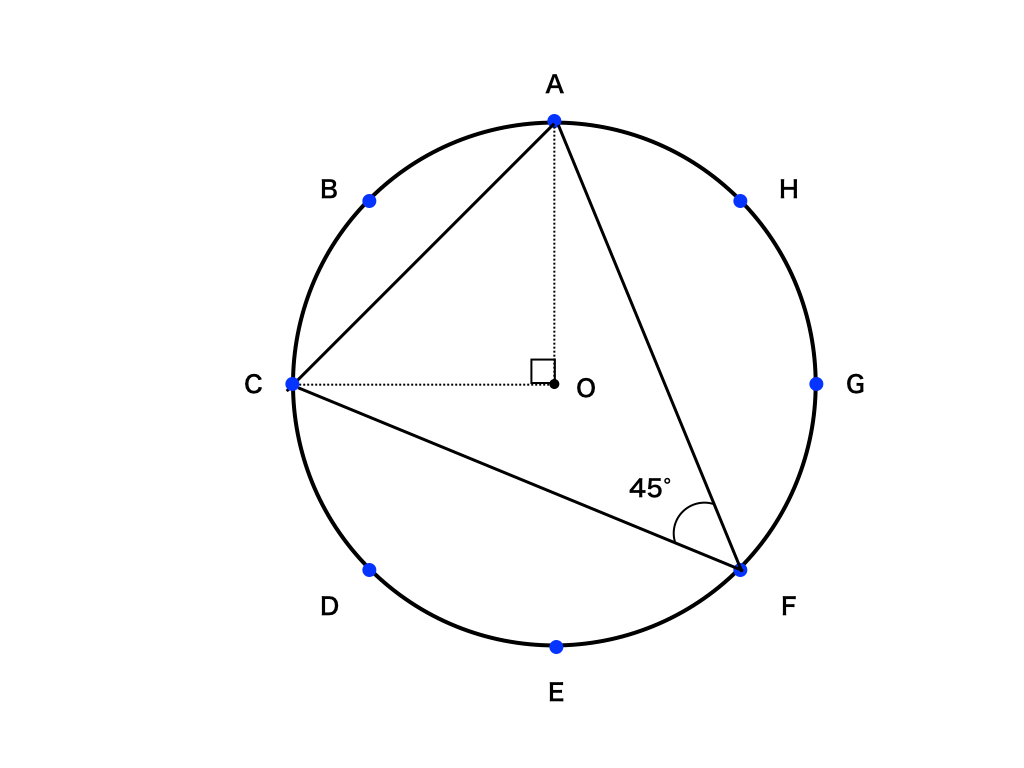
全ての面積を工夫して求められたでしょうか？

この種の問題は、場合の数と確率の単元と融合してよく出題されるので、そのことも覚えていおきましょう。

まとめと三角比の応用・関連記事へ

・三角比のまとめ

・三角比の表は有名角45°,60°,30°などを頭に入れて、還元公式（の記事の方法）を使ってその場で導くようにする

・正弦定理、余弦定理はどういったときに、どちらを使うのかを意識しながら類題を解く

（円の半径や内接円が出てきたら、正弦定理を使うことが多く、２辺とその間の角が与えられている（or簡単に求められる）ときは余弦定理を使うことが多いです。）

三角関数と三角比の関連記事（＋物理基礎への応用）

・「力学と三角比の関係」について、今回の記事の内容を踏まえて、「物理基礎の力学でどのように三角比を使うのか」←の記事でまとめています。

・一つ上のレベル（数２の三角”関数”）に進みたい人は、「三角関数の公式のまとめ」の記事を読み進めてください。

今回も最後までご覧いただきまして、ありがとうございました。

当サイト「スマホで学ぶサイト、スマナビング！」では、記事のリクエストや、ご質問・ご意見を募集しています。

また、snsでいいね！やシェア、Twitterのフォローをしていただけると助かります。