微分の定義と基本公式をチェック
数学Ⅲに入って微分の範囲に入ると、一見これまでの数2の微積分とは次元が違う、複雑な式が並んでいます。
しかし、それも最初だけです。実際には数2と内容は大きく違いません。
この記事の『微分の定義』さえしっかりと理解できれば、扱う関数が複雑に見えても対応できます。
ぜひじっくり読んで基礎を固めて下さい。
※先に、数学2の微分を復習しておきたい人のために
→「【数学2】三次関数のグラフ・増減表・極値の求め方【微分法】」を作成しました。
目次(タップした所へ飛びます)
微分公式まとめと定義
・微分とは何か
・変化量Δxの極限をとる
・微分の回数とn階微分
↑ここまで微分の定義/基礎用語
ここから基本公式↓
・微分の重要公式(和/積/商の微分法)
・数学Ⅲの微分の基本公式
・次回予告
微分とは何か(定義とイメージ)
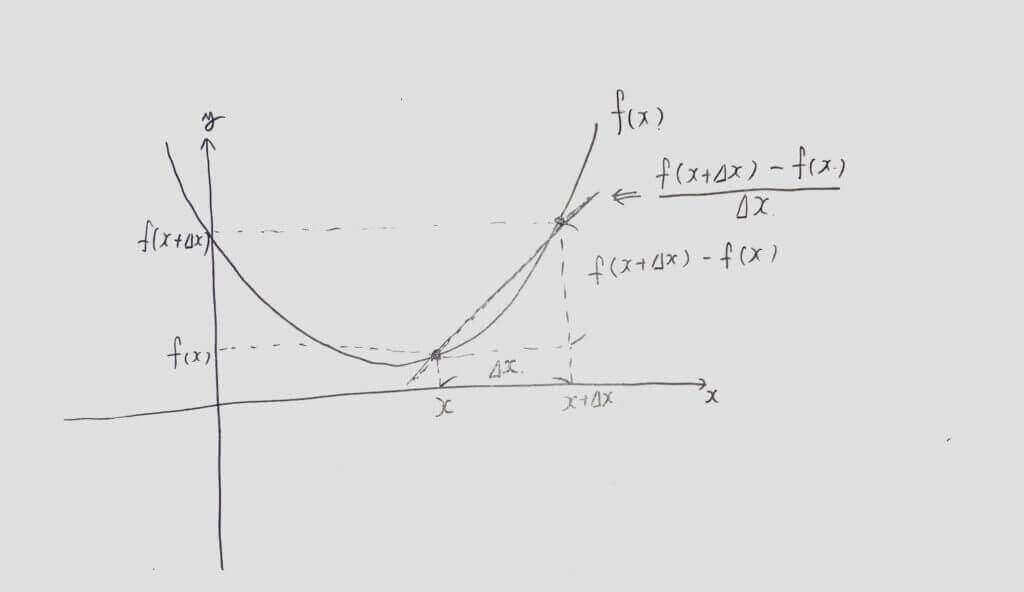
関数f(x)を考えたとき、f(x)のx座標をΔxだけ変化させたf(x+Δx)とf(x)の差である、f(x+Δx)-f(x)を考えてみます。
これはΔxという変化量に対する関数f(x)の変化量を表す式で、xy座標上のグラフy=f(x)におけるy座標の差を表しています。
$$そして、次に\frac {f(x+\Delta x) -f(x)}{\Delta x}を考えます$$
これはf(x+Δx)とf(x)の間のy座標の変化量をx座標の変化分(x+Δxーx)=Δxで割った数を表しています
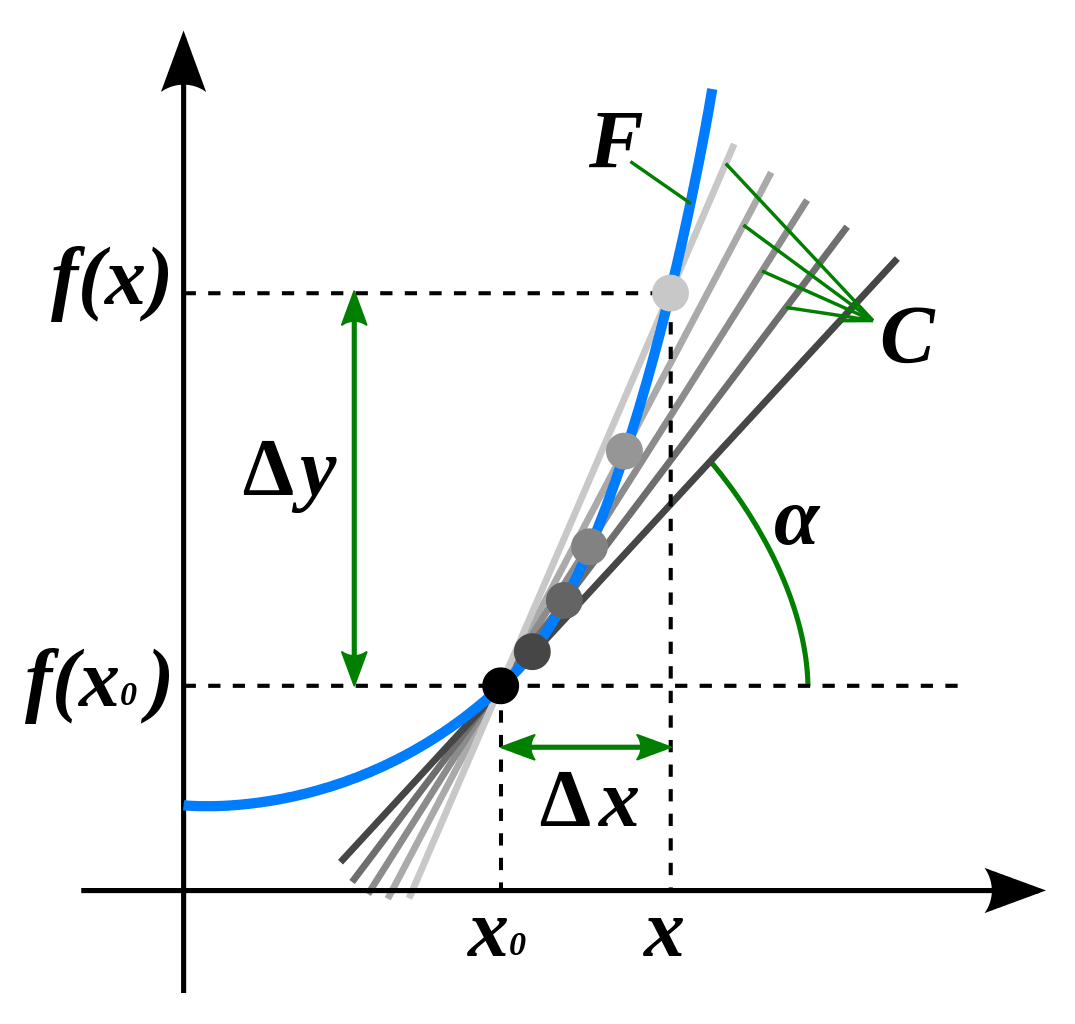
<図1>を見るとよく分かりますが、これは点(x,f(x))と点(x+Δx,f(x+Δx))を結ぶ直線の傾きを表します。
<図1>
Δxの極限をとる
では$$\lim _{\Delta x\rightarrow 0}\frac {f( x+\Delta x)-f(x) }{\Delta x}$$
すなわち、Δxを限りなく0に近付けると、この直接の傾きはどのように変化して行くのでしょうか?
考えてみると、徐々にΔxが小さくなると共にf(x+Δx)とf(x)のy座標の差も小さくなるので、最終的には、グラフy=f(x)上の点(x、f(x))における接線の傾きと同じになります。
<図2>参照。
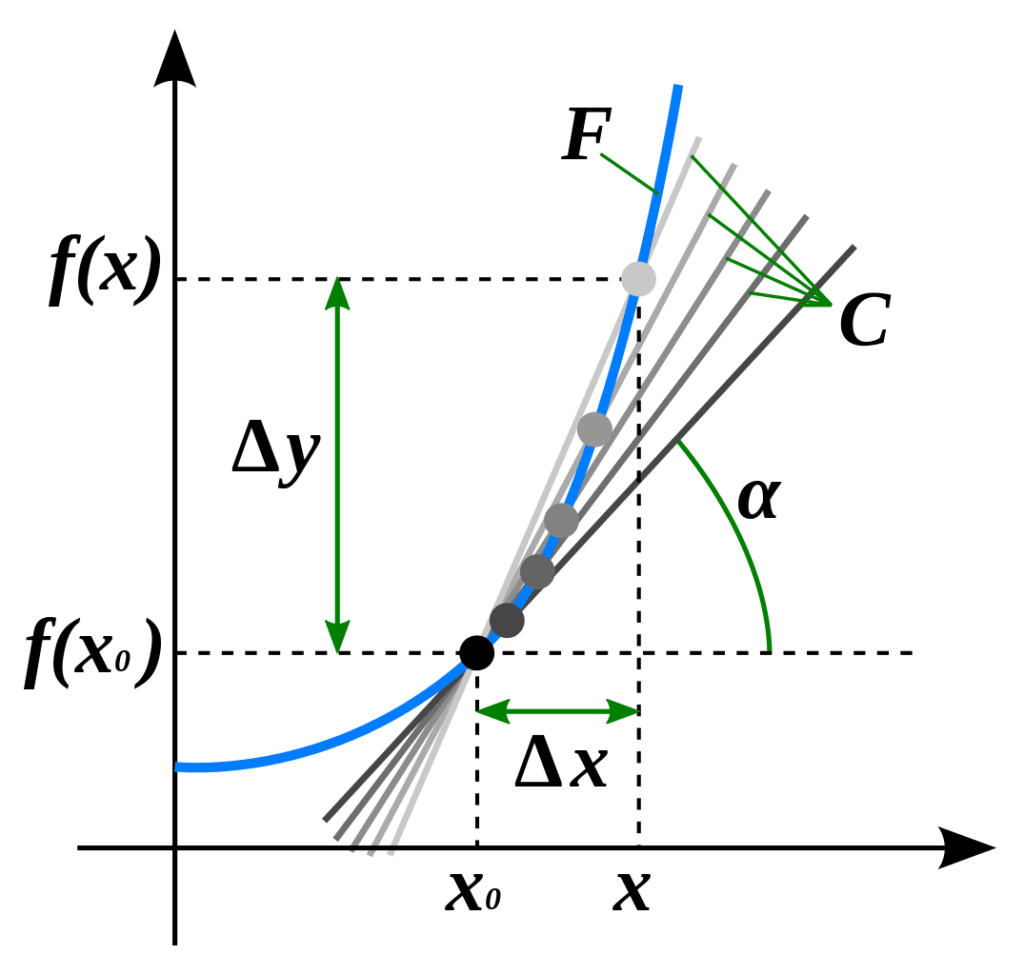
<図2:Δを極限まで小さくする>
この様に、Δxを限りなく0に近づけて関数の瞬間の変化量を求めることを「微分法」と呼びます。
そして、微分された関数:点xに於けるf(x)の傾きをf’(x)と記述します。
なお、このような極限値f’(x)が存在するとき、「f(x)はxで微分可能である」といいます。
詳しくは「微分可能な関数と連続な関数の違いについて」をご覧下さい。
また、微分することによって得られた関数f‘(x)に、
任意の値(ここではa)を代入し得られたf’(a)を微分係数と呼びます。
<参考記事:「微分係数と導関数を定義に従って求められますか?+それぞれの違い解説!」>
微分の回数とn階微分
微分は一回だけしか出来ないわけでは無く、多くの場合二回、三回と連続して何度も行うことができます。
n(自然数)としてn回微分を行ったとき、一般にこの操作を「n階微分」と呼びます。
例えば3回微分すれば「三階微分」です。「三回微分」ではないことに注意しましょう。
(回と階を間違えないように!)
微分法の重要公式
ここでは数3で初めて出てくる関数の”和・積・商の微分法の重要公式”を紹介します。
積と商の微分公式
\((f(x)) +g(x)) '=f'(x)+g'(x)\)
積の微分法:\(( f_{x} \cdot g( x))^{'}=f'(x)g(x)+f(x) g'(x)\)
商の微分法$$( \frac {f(x)}{g(x)})^{'}=\frac {f'(x)g(x)-f(x)g'(x)}{(g(x))^{2}}$$
積の公式は微分の定義に従って丁寧に式変形をしていくことで示せます。
$$商の公式はf(x) × \frac {1}{g( x) }と見て$$、
1/g(x)の微分を定義に従って計算することで証明可能なので、
練習 +公式を定着させる為に一度自分で導出してみてください。
数学Ⅲ範囲の微分の基本公式
ここからは、数学Ⅲの微分法に於いて必要不可欠な公式を紹介していきます。
まずはxの◯乗の微分についてです。
定数の微分や、aが正の整数、つまり多項式のときは高2の微分範囲のものなので高3生は慣れている方もいるかもしれません。
しかし、a=1/2の時や、a=-1の時は、無理関数や分数関数となり、初めて扱う事になると思います。
比較的頻出の関数なので演習をつんで感覚をつかんでおく事をオススメします。
$$\frac {d}{dx}x^{a}=ax^{a-1}$$
しかしながら、やはり数Ⅲのメインの微分公式は三角関数、指数関数、対数関数の場合です。
それぞれの公式を見てみましょう。
<三角関数の微分>
$$\frac {d}{dx}\sin x=cosx$$
$$\frac {d}{dx}\cos x=-\sin x$$
$$\frac {d}{dx}\tan x=\frac {1}{\cos ^{2}x}$$
これらの基本公式は、微分の定義に従って加法定理と有名な極限値から証明可能です。
”sin x”と”cos x”の微分で注目すべきことはどちらも「周期性を持っている」ということです。
三角関数は手計算で確かめてみるとすぐにわかりますが、四階微分を行うと元の関数に戻ります。
<指数・対数関数の微分>
$$\frac {d}{dx}e^{x}=e^{x}$$
$$\frac {d}{dx}\log x=\frac {1}{x}$$
また、指数関数、特に底が自然対数の底(=e)の場合は微分しても同じ関数が出てくるという不思議な性質をもっています。
この不思議な数e(自然対数の底=ネイピア数については、column:ネイピア数って何の為にあるの?の記事で解説しています。興味があればご覧下さい。)
そして最後の式より、対数関数を微分すると、分数関数に帰着するという性質がわかります。
(※数学IIIで対数関数が出てきた時、底の記述がない場合は、底=eである自然対数として扱います)
微分の定義・基礎まとめ
今回は微分の基本的な考え方と各種の有名関数の微分を紹介しました。
次回は、これらを使って「合成関数の微分法」や「対数微分法」など少し発展的な微分法を解説していきます。
対数微分;合成関数微分へ(続編)
続編作成しました!
是非ご覧下さい!
今回も最後まで読んで頂きましてありがとうございました。
お役に立ちましたら、snsボタンよりシェアお願いします。_φ(・_・
お疲れ様でした。質問・記事について・誤植・その他のお問い合わせはコメント欄又はお問い合わせページまでお願い致します。

