二次形式の標準形の意味と変換手順を解説!主成分分析の為の基礎数学

2020-02-04 2020-02-07

執筆者・編集者プロフィール

安田周平

■個別指導塾YES/YESオンラインスクール塾長・船場物産株式会社代表取締役社長。
★塾長及びyesの講師陣がマンツーマンで英検・TOEIC・TOEFL・数検・大学入試対策(英・数・物・化・情報1)を指導します。(東京・大阪・オンライン)
★詳細は以下のリンクよりお問い合わせください。
■『スマナビング！を見て受講希望』とお伝えいただければ、特別優待を準備しています。

＞＞個別指導塾YES公式HP＜＜

二次形式の意味と標準化

＜この記事の内容＞：線形代数で登場する「二次形式」の基本的な知識から、その標準化の手順を一歩一歩丁寧に解説しています。(二次形式はその応用・関連分野としてのPCAを理解するために重要な知識の一つです。今後数回に分けて詳しく見ていきます）

目次(タップした所へ飛びます)

二次形式とは
- 二次形式の定義と具体例
- 行列での二次形式の表現と例
二次形式の標準形
- 標準化の手順と直交行列の復習
- (具体例)二次形式を標準形にする手順
標準化を視覚的に理解する
- 前;斜め向きの楕円
- 後:軸と長軸/短軸が一致
  - 主軸変換：前後を重ねてみると・・・
二次形式まとめと主成分分析へ
- 関連記事と〜共分散行列へ〜

二次形式とは

二次形式とは、式中の変数の次数が全て二次である式のことを言います。

ex)$5x^{2}-4xy+5y^{2}$は、２次の”x”、（１次のx・１次のy(＝"xy"←２次)）、２次の”y”のみで構成されているので『二次形式』と言えます。

二次形式の定義と具体例

もう少し一般的な定義をシグマ（参考：「シグマ記号と数列の和の意味」）を使って表してみます。

xの二次形式

$$\sum ^{n}_{i=1}\sum ^{n}_{j=1}a_{ij}x_{i}x_{j}$$

($a_{ij}=a{ji}$であるものとする)

これだけ見ると嫌になりそうですが、例えばn=2の時を考えると($n=3,4,\cdots$ でも同様です）

$$\sum ^{2}_{i=1}\sum ^{2}_{j=1}a_{ij}x_{i}x_{j}$$

まず片方のシグマを計算して

$$\sum ^{2}_{i=1}(a_{i,1}x_{i}x_{1}+a_{i,2}x_{i}x_{2})$$

残りのシグマを計算する

(途中で出てくる$a_{1,2}x_{1}x_{2}はa_{2,1}x_{1}x_{2}$と同じとする）

・・・これを行列の成分として考えると、対角成分の右上・左上が同じカタチをした【対称行列】と呼ばれる非常に重要な行列となります。

これについては、次回「(作成中です)：実対称行列とエルミート行列の性質」で詳しく扱いますが、頭の片隅に置いておいてくださいください。

$=a_{1,1}x_{1}^{2}+2a_{1,2}x_{1}x_{2}+a_{2,2}x_{2}^{2}$

上の式と例で挙げた(ex)$5x^{2}-4xy+5y^{2}$を対応させてみてみると、

$a_{1,1}=5,a_{1,2}=-2,a_{2,2}=5,x_{1}=x,x_{2}=y$となっていることが分かるでしょうか？

このように、二次形式を２つのシグマ記号で簡潔に書き表したものが『枠でくくった部分の式』なので、ヤヤコシクなったら具体的な数字を入れて確かめてみましょう。

行列での二次形式の表現と例

上で紹介した二次形式の例(ex)$5x^{2}-4xy+5y^{2}$を『行列の積のかたち』であらわしてみます。

（ここからいよいよ『線形代数』らしくなってきます。復習したい方は→「行列どうしの掛け算（積）を分かりやすく」）

各係数を比較して、次の３つの行列（２つの列・行ベクトルと１つの正方行列）の積にすれば上手く元の二次形式になります。

$$\begin{bmatrix}
x & y
\end{bmatrix}\begin{bmatrix}
a_{11} & a_{12} \\
a_{12} & a_{22}
\end{bmatrix}\begin{bmatrix}
x \\
y
\end{bmatrix}$$

より、$\begin{pmatrix}
x & y
\end{pmatrix}\begin{pmatrix}
5 & -2 \\
-2 & 5
\end{pmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix}$

これが正しいのかは実際に展開していくとチェックできます。

二次形式の標準形

さて、ここまで扱ってきた2次形式は“xy”という項が邪魔をして、我々が知っている「二次曲線の形（楕円)」になりません。そこで、$ax^{2}+by^{2}$の形にする作業を”標準化”と言います。

標準化の手順と直交行列の復習

2次形式の標準化には、「直交行列U」を用います。詳しくは→「直交行列の性質」

(具体例)二次形式を標準形にする手順

では実際に、先ほどから例示している$5x^{2}-4xy+5y^{2}=8\cdots (※)$という二次形式を標準化していきます。

途中少し複雑なところもありますが、とりあえず『流れ』を頭に入れるようにしてください。

（以下で固有値・固有ベクトルを扱います。参照：「固有値問題の解説記事」）

固有方程式を解く(step1)

行列の積で表した（※）の左辺は次のようになり、中心の正方行列$\begin{bmatrix}
5 & -2 \\
-2 & 5
\end{bmatrix}$をAとします。

$\begin{bmatrix}
x & y
\end{bmatrix}\begin{bmatrix}
5 & -2 \\
-2 & 5
\end{bmatrix}\begin{bmatrix}
x \\
y
\end{bmatrix}$

$|T|= |A-\lambda E|=0$を解くと、

$\begin{vmatrix}
5-\lambda & -2 \\
-2 & 5-\lambda
\end{vmatrix}=\lambda^{2}-10\lambda+21$

よって、固有値λ＝3,7。

固有ベクトルを求め正規化する(step2)

（Ⅰ）：λ＝３の場合

ここから、それぞれの固有ベクトルを求めていきます。

$\begin{bmatrix}
2 & -2 \\
-2 & 2
\end{bmatrix}\begin{pmatrix}
m_{1} \\
m_{2}
\end{pmatrix}=\begin{pmatrix}
0 \\
0
\end{pmatrix}$

上の式を展開して$m_{1}-m_{2}=0$

ランクが１なので、(「階段行列とランク・自由度を解説」）

$m_{2}=k_{1}とおくとm_{1}=k_{1}$

したがって、$\vec{x_{1}}=k_{1}\begin{pmatrix}
1 \\
1
\end{pmatrix}$

ここで、ノルムを１にする：つまり正規化を行います。$\left(||\vec{x_{1}}||\right)=\sqrt{2}$だから、

$k_{1}=\frac{1}{\sqrt{2}}$と置けば良いことがわかります。

よって$$\vec{x_{1}}=\frac{1}{\sqrt{2}}\begin{pmatrix}
1 \\
1
\end{pmatrix}$$

が求まりました。

（Ⅱ）：λ＝７の場合も上の同様に進めていきます。

$\begin{bmatrix}
-2 & -2 \\
-2 & -2
\end{bmatrix}\begin{pmatrix}
n_{1} \\
n_{2}
\end{pmatrix}=\begin{pmatrix}
0 \\
0
\end{pmatrix}$

結果、$$\vec{x_{2}}=\frac{1}{\sqrt{2}}\begin{pmatrix}
-1 \\
1
\end{pmatrix}$$

となります。

直交行列Uと$U^{-1}$で挟む:$U^{-1}AU$(step3)

以上の結果から、直交行列$U＝\frac{1}{\sqrt{2}}\begin{pmatrix}
1 & -1 \\
1 & 1
\end{pmatrix}$となって、AをUの逆行列を左から、Uを右から挟んであげることで

$U^{-1}AU=\begin{pmatrix}
3 & 0 \\
0 & 7
\end{pmatrix}$

(対角成分は固有値となります）

変数変換して二次曲線の形へ(step4)

最後に、”x”と”y”で表されていた（※）の二次形式を【x'とy'】に変換します。

列ベクトル：$\begin{pmatrix}
x \\
y
\end{pmatrix}=U\begin{pmatrix}
x' \\
y'
\end{pmatrix}$と行ベクトルで$\begin{bmatrix}
5 & -2 \\
-2 & 5
\end{bmatrix}$を挟むために、$\begin{pmatrix}
x \\
y
\end{pmatrix}$を転置させます。

$\begin{pmatrix}
x \\
y
\end{pmatrix}^{T}=\begin{pmatrix}
x' & y'
\end{pmatrix}U^{T},かつU^{T}=U^{-1}$

（∵）直交行列の性質

より、$\begin{bmatrix}
x & y
\end{bmatrix}\begin{bmatrix}
5 & -2 \\
-2 & 5
\end{bmatrix}\begin{bmatrix}
x \\
y
\end{bmatrix}$

の両側のベクトルを置き換えていきます。

$\begin{bmatrix}
x' & y'
\end{bmatrix}U^{-1}\begin{bmatrix}
5 & -2 \\
-2 & 5
\end{bmatrix}U\begin{bmatrix}
x' \\
y'
\end{bmatrix}$

ここで、$U^{-1}AU=\begin{bmatrix}
3 & 0 \\
0 & 7
\end{bmatrix}$だったので（step３より）

５つ並んだベクトル・行列の積のうち真ん中の三つが消えて最終的に

$\begin{bmatrix}
x' & y'
\end{bmatrix}\begin{bmatrix}
3 & 0 \\
0 & 7
\end{bmatrix}\begin{bmatrix}
x' \\
y'
\end{bmatrix}$となります。これを行列の積のルールに沿って展開していくと、

$\begin{bmatrix}
3x' & 7y'
\end{bmatrix}\begin{bmatrix}
x' \\
y'
\end{bmatrix}=3x'^{2}+7y'^{2}$

あとは、右辺＝８だったので、$3x'^{2}+7y'^{2}=8$とすると確かに”xy”の項が消えて上手く楕円の式（二次曲線の式）の形にすることができました。

（お疲れ様でした！あとは今回の結果の幾何的な意味を見ていきましょう。この複雑な操作が非常に美しい意味を持つことが分かるかと思います。）

標準化を視覚的に理解する

さて、ここまで少し（かなり？）大変でしたが、二次形式$5x^{2}-4xy+5y^{2}=8$を$x^{2}+y^{2}=8$に”標準化”することが出来ました。

これは一体どのような意味を持つのか、視覚的にとらえてみます。

前;斜め向きの楕円

まずは標準化する前の(※)の二次形式を座標平面上に描くと

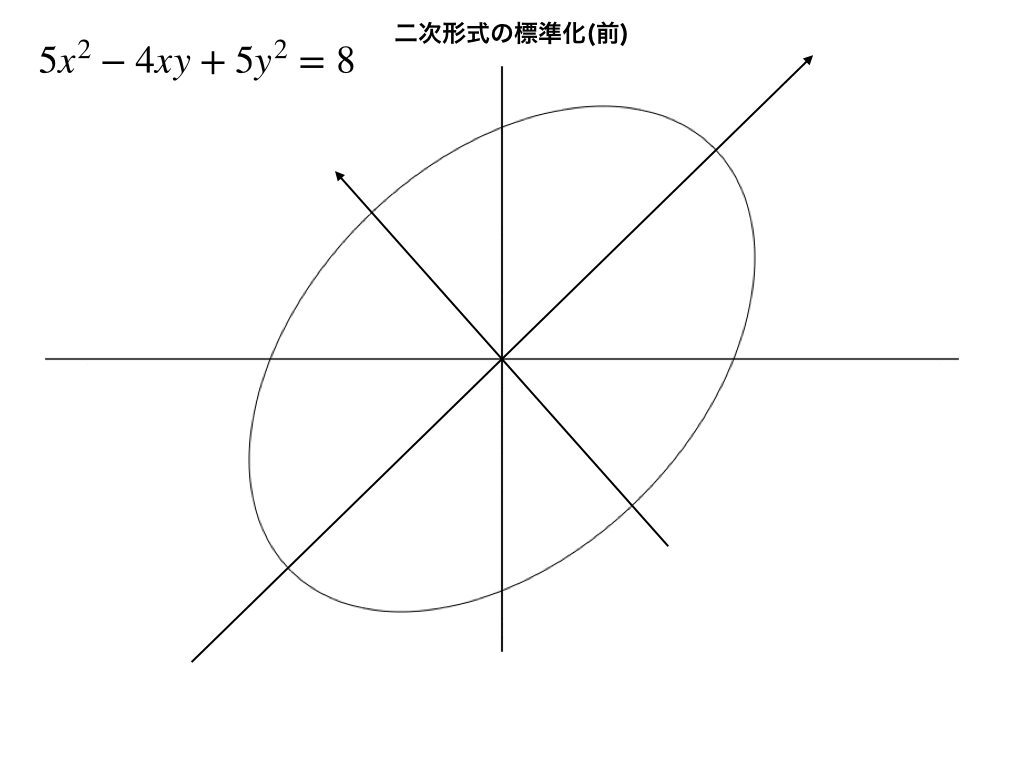
形は楕円ですが、長短軸が斜めになっています。

後:軸と長軸/短軸が一致

さあ、標準化後の$x^{2}+y^{2}=8$を同様に描くと・・・

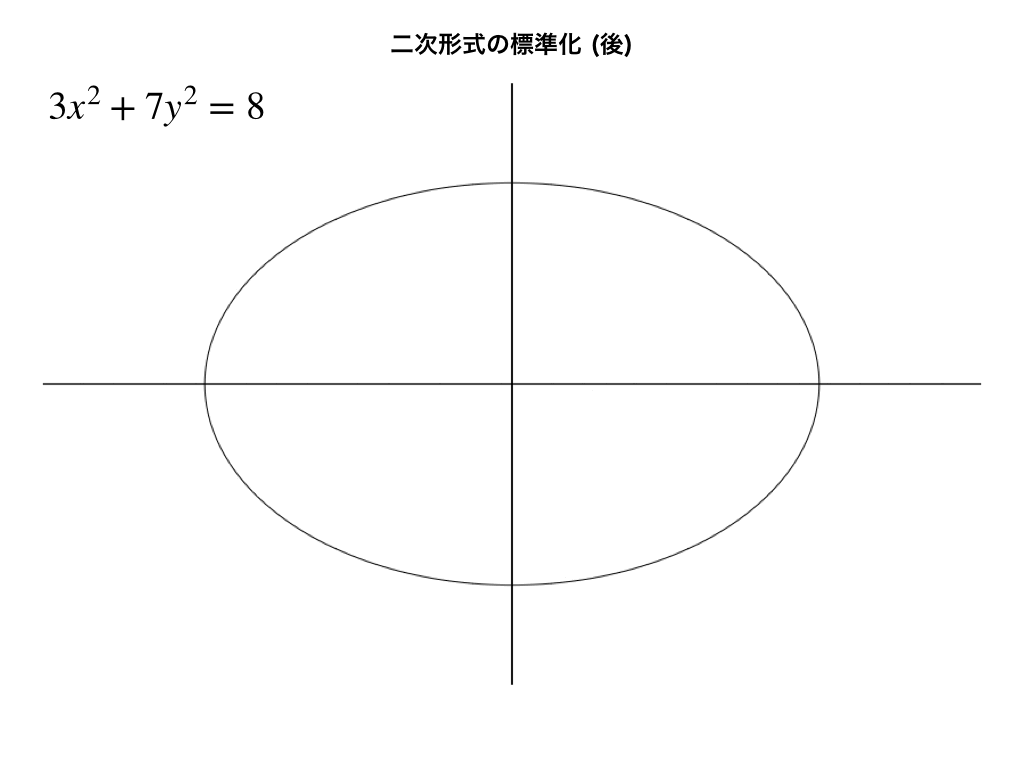
主軸変換：前後を重ねてみると・・・

青色で示した標準化後の$x^{2}+y^{2}=8$青色の楕円は元々の$5x^{2}-4xy+5y^{2}=8$と

・大きさ

・角

が同じで軸のみが回転している様子がわかります。

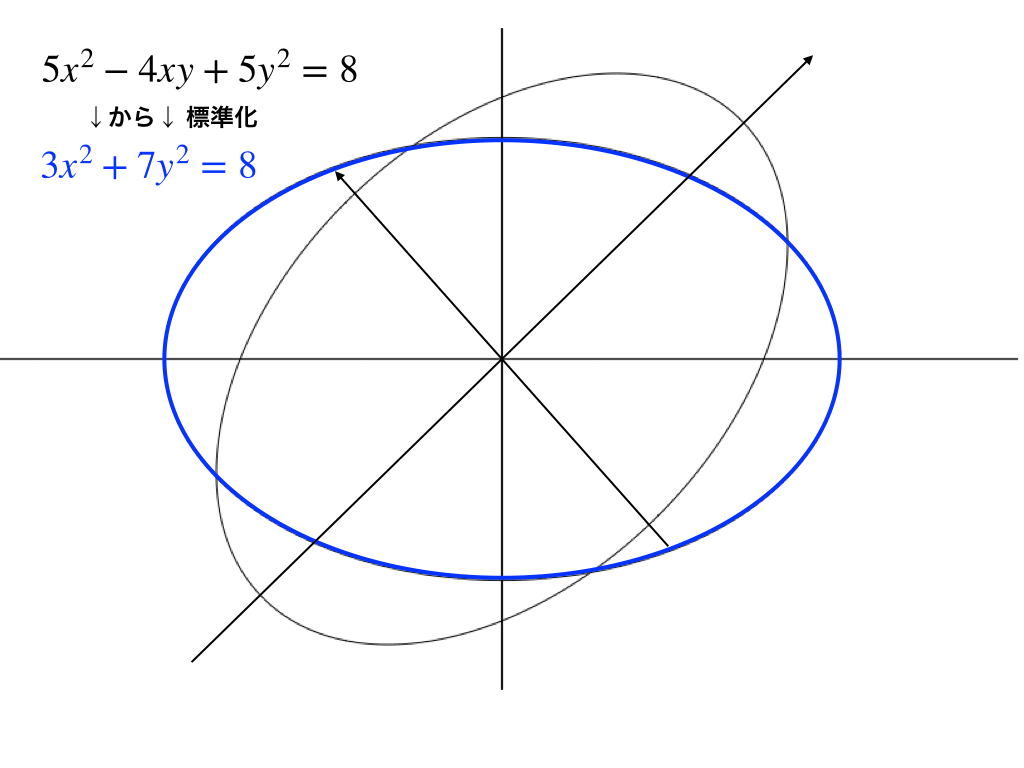
＜二次形式の変換前後＞

二次形式まとめと主成分分析へ

・今回は直交行列を用いて二次形式を変換する作業を行いました。

・手順が多く大変なので、実際に手を動かして練習したりテキストなどで問題を解いて慣らせていきましょう。

・最後にグラフで見た『主軸』の変換（二次曲線の回転）が今後学習する『主成分分析』の基礎の一つとなります。機械学習の理論を勉強している方はこのイメージを頭に入れておきましょう。