ベクトルの共線条件と共面条件
今回は、「空間ベクトルの共面条件」を解説していきます。
目次(タップした所へ飛びます)
共線条件と共面条件
共面条件の前に、平面ベクトルでの共線条件をおさらいしておきます。
共線条件
共線条件とは、三点が一直線上に存在するときに成立する条件の事で、
例えば点Bが直線AC上にある時、
AB=kAC (kは実数) の様に始点(ここではA)を揃えると、
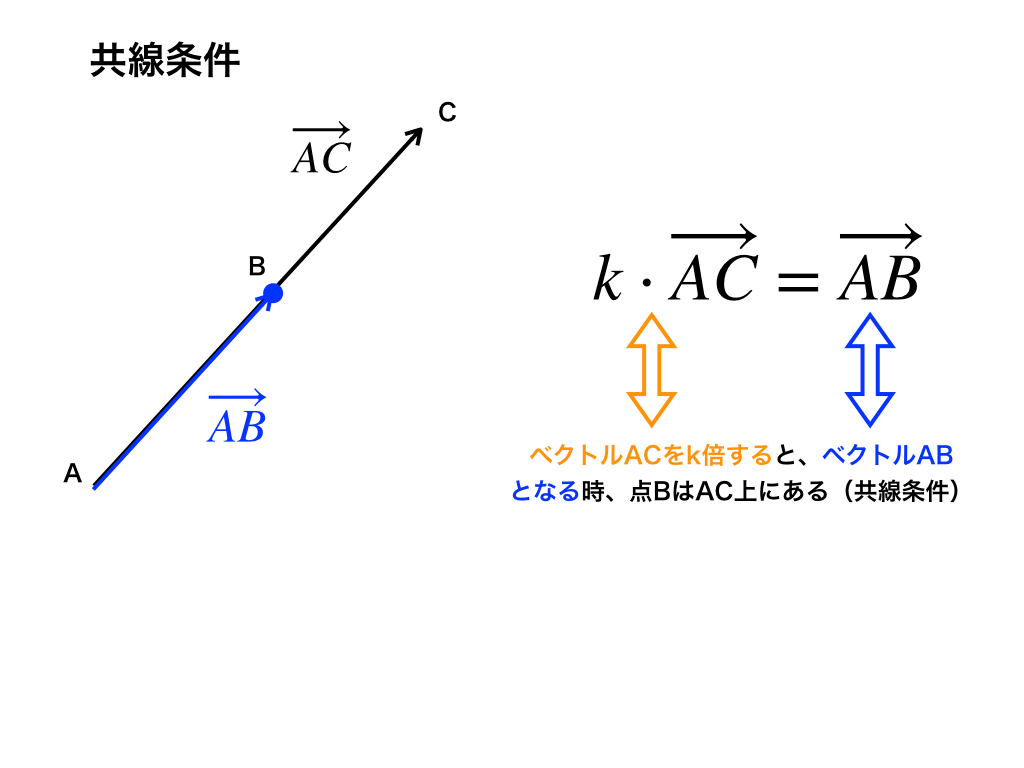
ABベクトルはACベクトルのk倍という式が成立します。これがベクトルでの共線条件です。(参考:「複素数平面でのなす角・共線条件」)
共面条件はどの様な条件でしょう?
共線が共面に変わっているので、線から面へ一つ次元が上がっています。
共線条件は3点が同一直線上だったので、共面条件は4点が同一平面上にある条件と言えます。
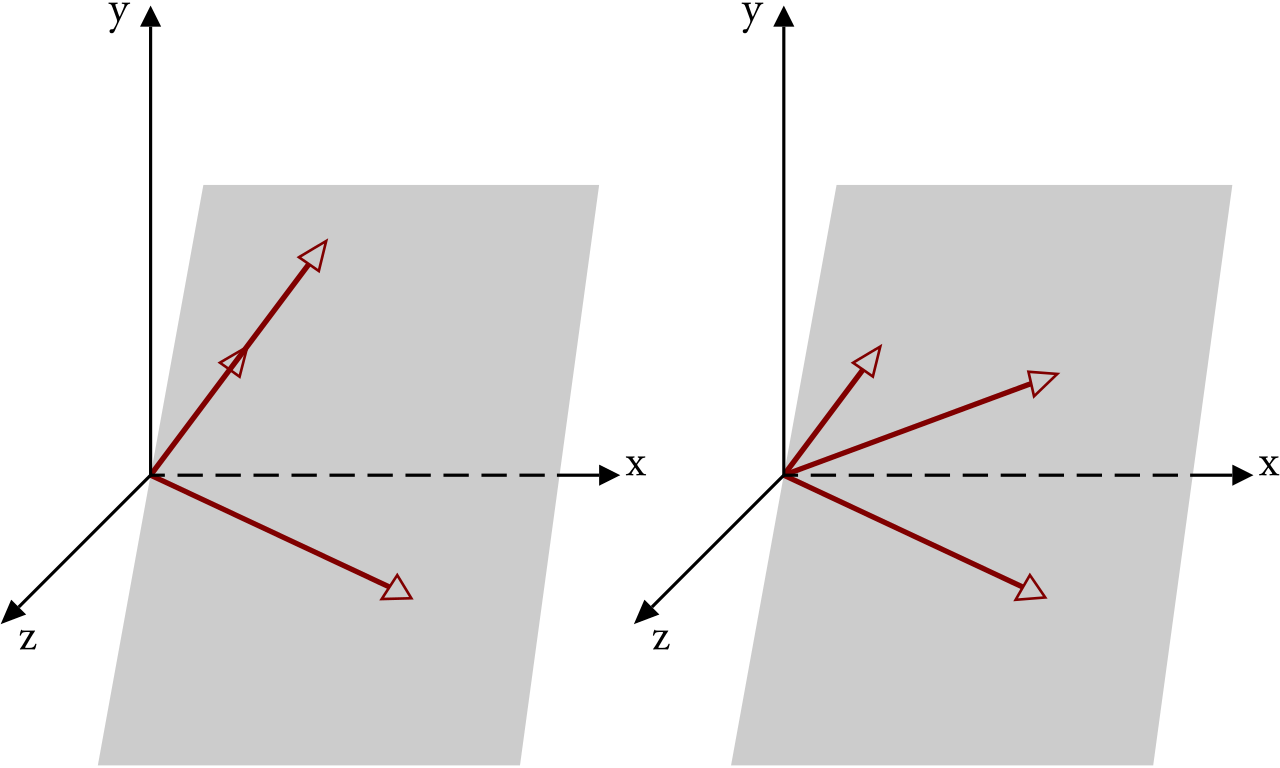
例)点Dが平面ABC上にある条件は、一次独立*なベクトルABとベクトルACを使って
(1)AD=sAB+tAC (s、tは実数)という式が成立します。
$$\vec {AD}=s\vec {AB}+t\vec{AC}$$
もしくは、
(2)平面ABCの外に点Oを取った時、OD=αOA +βOB +γOC
$$\overrightarrow {OD}=α \overrightarrow {OA}+β \overrightarrow {OB}+γ \overrightarrow {OC}$$
但し(α、β、γは実数かつ、α +β +γ=1**)
が成立します。
ちなみに(1)に点Oを導入してベクトルの分解を行うと、
$$( \overrightarrow {OD}-\overrightarrow {OA}) =s(\overrightarrow {OB}-\overrightarrow {OA}) +t( \overrightarrow {OC}-\overrightarrow {OA}) $$
$$\overrightarrow {OD}=( 1-s-t) \overrightarrow {OA}+s\overrightarrow {OB}+t\overrightarrow {OC}$$
(ODー OA)=s(OBー OA)+t(OCー OA)⇔
OD=(1-s−t) OA +s OB +tOC となり、
(1-s−t)=α 、s=β、t=γ と置くと
α +β +γ=(1-s−t)+s +t=1 より、(2)と一致します。
*一次独立について
一次独立とは、今回の例で言えばABとACが並行ではなく、
同時にAB= AC≠0ベクトルであることを言います。
一次独立について詳しくは「ベクトルの一次独立って何?」、「位置ベクトルって何?」をご覧下さい。
**α +β +γ=1
係数の和が1の法則については、「係数の和が1になる条件と理由」にて解説しています
ここまでの説明では実際どの様に役に立つか分かりにくいと思うので、例題を見ていきます。
共面条件の確認例題
例題:四面体OABCがあり、OAを2:1に内分する点をD、
OBを2:1に内分する点をEとする。
$$三角形ABCの重心を点Gとして、\vec {OG}$$
と平面DECとの交点をFとする時、
$$\vec {OF}を\vec {OA},\vec {OB},\vec {OC}で表せ。$$
解説
$$解答解説:条件より、\overline {OD}=\frac {2}{3}\overrightarrow {OA}、\overline {OE}=\frac {2}{3}\overrightarrow {OB}$$
重心GへのOからのベクトルOGは、
$$\vec {OG}=\frac {\vec {OA}+\vec {OB}+\vec {OC}}{3}$$
ここで、ベクトルOGは点Fを通るので、共線条件より、
$$\overrightarrow {OF}=k\overrightarrow {OG}=\frac {k}{3}\overrightarrow {OA}+\frac {k}{3}\overrightarrow {OB}+\frac {k}{3}\overrightarrow {OC}$$
ここで、ベクトルOFは平面DEC上の点だから、共面条件より、
$$\vec {OF}=s\vec {OD}+t\vec {OE}+u\vec {OC}と表せ、$$
(s+t+u=1)
$$また\overrightarrow {OF}=\frac {2s}{3}\overrightarrow {OA}+\frac {2t}{3}\overrightarrow {OB}+u\overrightarrow {OC}と出来る。$$
ここで、ベクトルOA、OB、OCは一次独立より、2通りで表されたベクトルOFの各係数を比較して、
$$\frac {k}{3}=\frac {2}{3}s,\frac {k}{3}=\frac {2}{3}t、\frac {k}{3}=u$$
$$更にs=\frac {k}{2},t=\frac {k}{2},u=\frac {1}{3}kをs+t+u=1に代入すると、$$
$$\begin{aligned}\frac {k}{2}+\frac {k}{2}+\frac {1}{3}k=1\\
⇔ 3k+3k+2k=6\\
⇔ 8k=6\\
⇔ k=\frac {3}{4}\end{aligned}$$
$$よって、\vec {OF}=\frac {1}{4}\vec {OA}+\frac {1}{4}\vec {OB}+\frac {1}{4}\vec {OC}$$
この問題の応用編を作成しました!
→「空間ベクトルの復習に最適!共面条件を使う良問」を見てみる。
共線条件・共面条件まとめ
このように、空間ベクトルでも基本的にやっていることは平面ベクトルの時と同じで、そのほとんどが式変形(ベクトルの分解等)で解けてしまいます。
空間図形の問題をほぼ機械的に解いていける事がベクトルの最大の強みと言えます。
今回は、解説中に関連記事の紹介リンクを貼ってあるので、分からないところが出て来たら一旦その記事を読んでみて、戻って来てもらえると理解がスムーズに進むかと思います。
ベクトルの記事まとめ
ベクトルを1から網羅→「ベクトルとは?ゼロから始める徹底解説記事9選+α」を読む。
今回も最後までご覧いただき有難うございました。
質問・記事について・誤植・その他のお問い合わせはコメント欄、
又はお問い合わせページまでお願い致します。

