2交点を通る直線や曲線の式(図形と方程式3)
<この記事の内容>:円と円の交点を通る『直線や曲線・円の式』が、\(f(x,y)+k\cdot g(x,y)=0\)(kは実数で文字は何でも構いません)で表すことができる”理由”と、習得用の例題を通して”束(そく)”と呼ばれるこれらの式を学びます。
<関連する記事>:「図形と方程式1:円の式と弦の長さ」と「図形と方程式2:2つの円の共通接線と位置関係」をできれば先に確認しておいてください(特にこの単元が苦手な人)。
なお、記事の最後にも同時に読んでおきたい記事をまとめています。
目次(タップした所へ飛びます)
円の2交点を通る直線と曲線
まずはじめに、\(f(x,y)+k\cdot g(x,y)=0\)が成り立つことを示し、直線になる場合の解説→定着用問題の順に紹介していきます。
交点を通る線の式が成り立つ理由
ここでは、f(x,y)=(円の方程式)かつ、g(x,y)=(円の方程式)の場合を例にします。
以下の図のように、f(x,y)=で表される円の上にある点の座標をf(x,y)に代入すると0となります。
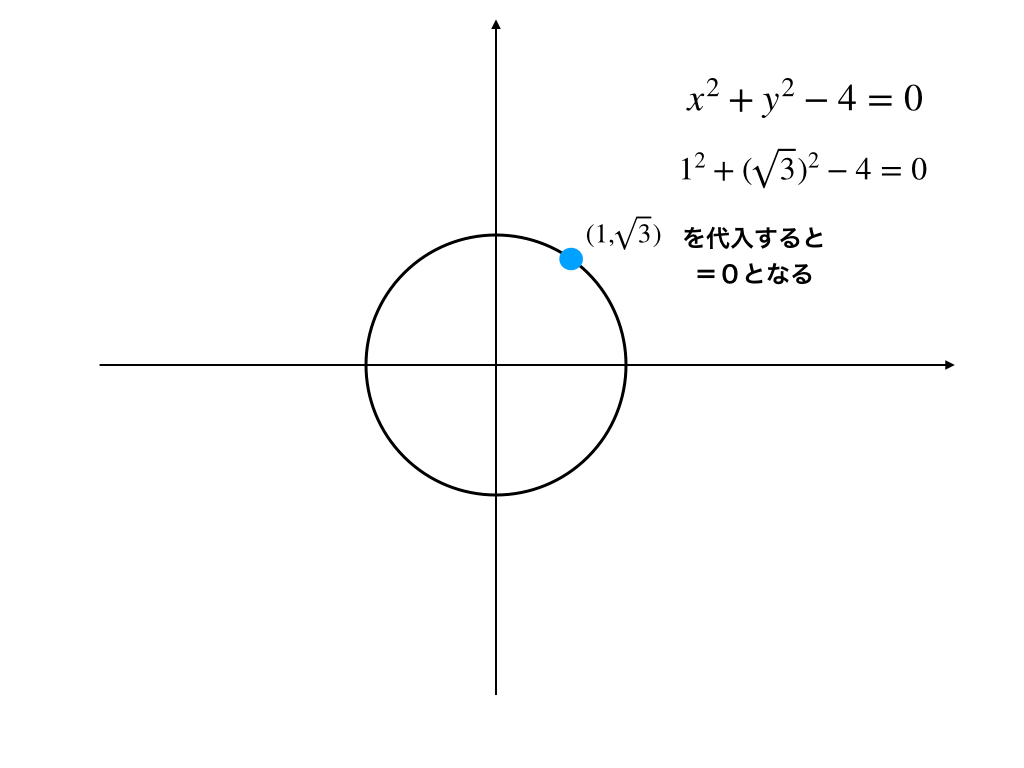
上の図のように、\(x^{2}+y^{2}-4=0\)の円上の点\(1,\sqrt{3}\)を代入すると\(1^{2}+(\sqrt{3})^{2}-4=0\)となります。
そして、2つの円の交点は当然それぞれの円上にあるので、座標を代入すると以下のように\(f(x,y)=0,g(x,y)=0\)であることが言えます。
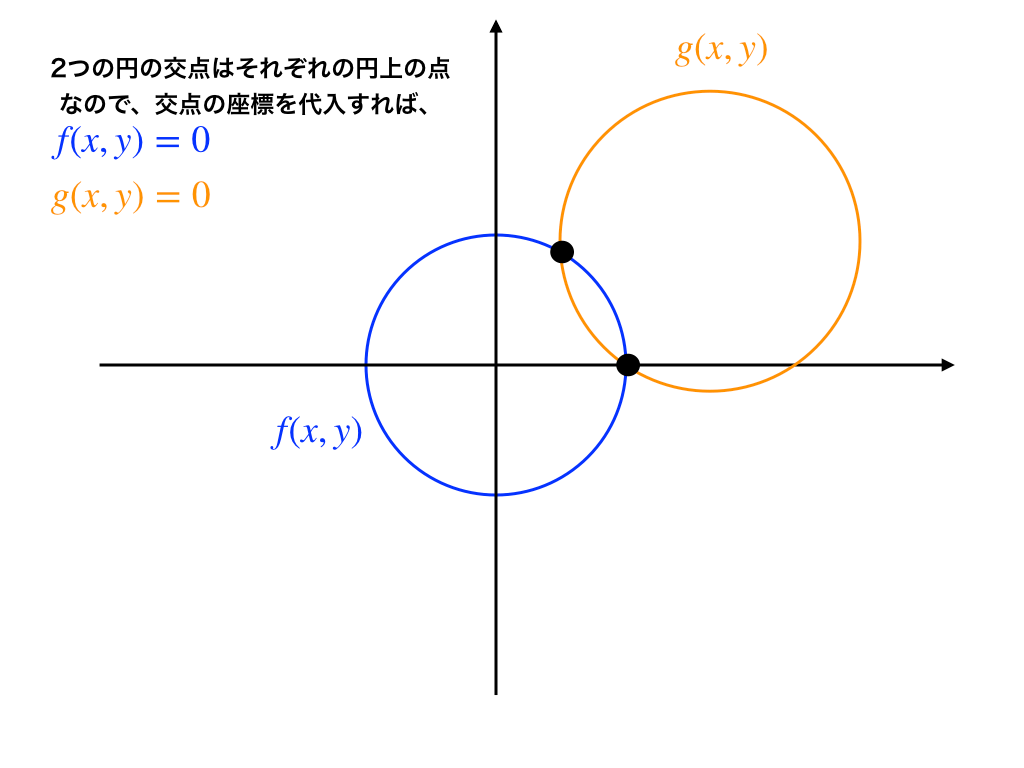
ここで、もう一度問題の式を見てみます。$$f(x,y)+k\cdot g(x,y)=0$$
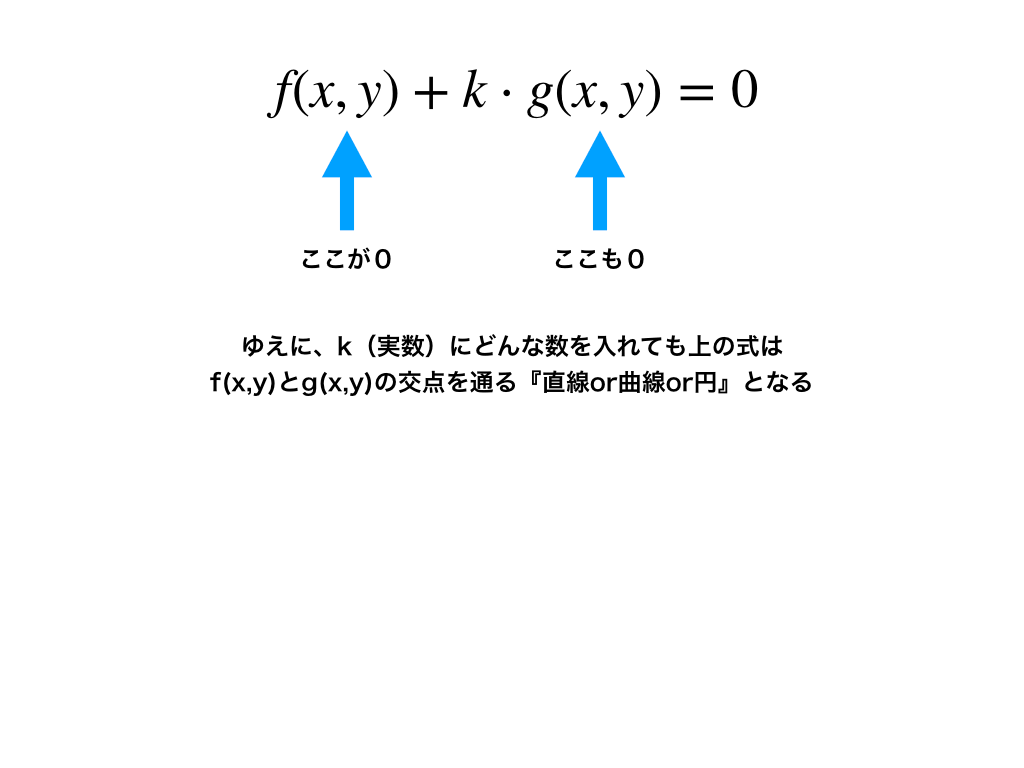
この式が”kの値にかかわらず”『2交点を通る全ての直線/曲線(但し、g(x,y)=0は除く)を表す』理由は、交点の座標を代入した時
以下のように『f(x,y)=0,g(x,y)=0』となり、\(0+k \times 0=0\)が成立するためなのです。
具体例で理解を深める/直線である為の条件
さて、\(f(x,y)+k\cdot g(x,y)=0\)の仕組みが何となく理解出来てきたでしょうか?
実際に問題を解いてみないとピンと来ない人もいるかと思うので、例題を使って定着させていきましょう。
(定着用例題)
:いま、xy座標平面上に\(x^{2}+y^{2}=4で表される円A\)と\((x-3)^{2}+(y-3)^{2}=9で表す事が出来る円B\)が存在する。
(1):この時円Aと円Bの交点を通る式を文字kを使ってあらわし、
(2):式が直線であるためのkの条件と、その直線の方程式を答えよ。
・・・
(例題解説)
:この問題はただ単に上の式のf(x,y),g(x,y)を具体的な円の方程式に当てはめるだけです。
(1):従って、\(x^{2}+y^{2}-4+k(x^{2}-6x+9+y^{2}-6y+9-9)=0\):円Bは一般形に展開しています。
もう少し式を整理して、\(x^{2}+y^{2}-4+k(x^{2}-6x+y^{2}-6y+9)=0\)・・・(答)
直線であるための”条件”
(2):(1)の式を(※)とすると、(※)が直線を表すときはどんな時でしょうか?
一般に直線の方程式は、\(ax+by+c=0\)のようになるので、(※)をこの形に持っていくことを考えます。
すなわち、不要な\(”x^{2}やy^{2}”\)を取りのぞけば良い事がわかります。
従って、 (※)のk=-1とすることでうまく二乗の部分だけが打ち消されます。
→\(x^{2}+y^{2}-4+(-1)\cdot (x^{2}-6x+y^{2}-6y+9)=0\)
→\(-4+6x+6y-9=0\)
→\(6x+6y-13=0\)が円A,円Bの交点を通る直線の方程式で、k=-1・・・(答)となります。
交点を通る直線/曲線(束:そく)の考え方のまとめ
今回扱った、\(f(x,y)+k\cdot g(x,y)=0\)の式は”円と円”だけでなく、
・”円と曲線”や
・”曲線どうし”など、
様々な交点を通る直線・曲線の方程式を表します。
この記事で基本的な仕組みと例を身につけたら、ぜひ問題集などを使って定着させてみてください。
図形と方程式シリーズと関連分野の記事一覧
〜図形と方程式シリーズ〜
>>シリーズ総まとめページ『図形と方程式の解法/解説記事のまとめ・公式集』<<
第一回:「円の方程式と直線が切り取る弦の長さ」
第二回:「2つの円の共通接線と位置関係」
第三回:「今ココです」
第四回:「軌跡と領域:0から学ぶ!軌跡の仕組み」
〜関連分野〜
ベクトル
複素数平面
・お問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。

