
数学A整数分野:<n進法の扱い方(n進法シリーズ第1回)>
今回はn進法の意味、10進法との変換、n進数での足し算/引き算/掛け算/割り算についてまとめていきます。
(2019/02/11更新)
続編・続々編を作成しました。この記事を読み終えた後にぜひご覧ください。
n進法シリーズ第二回:「n進法の一般化と応用問題の解き方」
第3回:「n進数と桁数の融合問題と不等式の使い方」
目次(タップした所へ飛びます)
n進法とは?
そもそもn進法とは、n個の数字や文字で数を表す方法で、n倍すると桁が一つ上がる性質があります。
例えば、普段我々は10進法を主に使っています。そこで実際に使っている数を書き出してみると、
0、1、2、3、4、5、6、7、8、9
たしかに0〜9の10個の数字で全ての数を表しています。
他にも、コンピュータの世界では2進法が使われているのは聞いたことがあるのではないでしょうか?
こちらもやはり、0、1 の2種類の数字で処理されます。
或いは“16進法”もデジタルな世界ではよく使われます。では、16種類も数字が存在しないのにどうやって16進法をあらわすのでしょう?
0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F
上記のように、なんと9の次にアルファベットのAを使って表す決まりになっています。例えば10進法で15ならば、16進法ではFと表せます。
更に身近な進数は、分秒を表す60進法や時間を示す24進法が挙げられます。
ただし、本来ならば60進法などは60種類の記号で表すべきなのですが、記号の種類が多すぎて現実的でない為、10進法で表記しています。
(この辺りに興味がある人は60進法等を調べて見て下さい。色々と興味深い歴史があります)
さて、そろそろ今回の本題「n進法と10進法、n進法の四則演算」に入ります。
10進法とn進法の相互変換
例えば7進法で「31054」と表記されても、10進法に慣れ親しんでいる我々はイマイチピンときません。そこで、
n進法で表記された数を10進法で表す
という作業をすると具体的に分かりやすくなります。
加えて、n進法同士で計算する際も、一旦10進法にしてあげることで解きやすくなる事があります。
$$では、実際に31054_{(7)}を$$
10進法で表す方法を学んでいきます。
数学では、特に10進法以外で数を表す時には、
その進法を右下にかっこを付けて書いておくことが多いです(ここでは、7と記してあるので7進数)
まず1桁目の4は、7進法でも10進法でも4です。
次に2桁目の5について考えてみます。
10進法では、1桁目が9の時、もう一つ足すと位が上がって10となりました。
同様に7進法では、1桁目が6の時に一つ足すと一つ位が上がって10となります。
従って7進法で2桁目が5という事は、5回繰り上がっているので、
10進法での「7」が5つある事と同じと考えることができます。
=7× 5 =35
3桁目は0なので、4桁目に進みます。
4桁目は「1」です。
これは、3桁目が一回繰り上がったことを意味します。
3桁目が1回繰り上がるという事は、2桁目が7回繰り上がった事と同じで、
それは、1桁目が7回×7回=49回繰り上がった事と同じです。
さらに、1桁目が一回繰り上がるのは7になった時なので、
まとめると、7進法表記において1000とは、7×49回=343。
つまり10進法表記では343と同じ数字であると言う事が出来ます。
最後の5桁目に進みます。5桁目は3、つまり4桁目が3回繰り上がったと言う事です。
以下同様に続きます・・・
これまでの流れでだいたい分かるかと思いますが、n進法を10進法に変えるには、
$$n進法の1桁目の数× n^{0}+n進法の2桁目の数× n^{1}$$
$$+n進法の3桁目の数× n^{2}+$$
$$・・・+n進法のk桁目の数× n^{k-1}$$
と言う操作をすれば良いのです。
$$これを31054_{(7)}に当てはめると、$$
$$4× 7^{0}+5× 7^{1}+0× 7^{2}+1× 7^{3}+3× 7^{4}となり、$$
$$結果的に31054_{(7)}を10進法で表すと$$
4+35+0+343+7203=7585 となります。
この変換について、詳しくは<n進数第二回:「もう1つのn進法の変換と応用問題」>でも解説しています。
10進法で表記された数をn進法で表す。
ここでは、10進法で表された数をn(例題では7進法)に変換する方法を図解します。
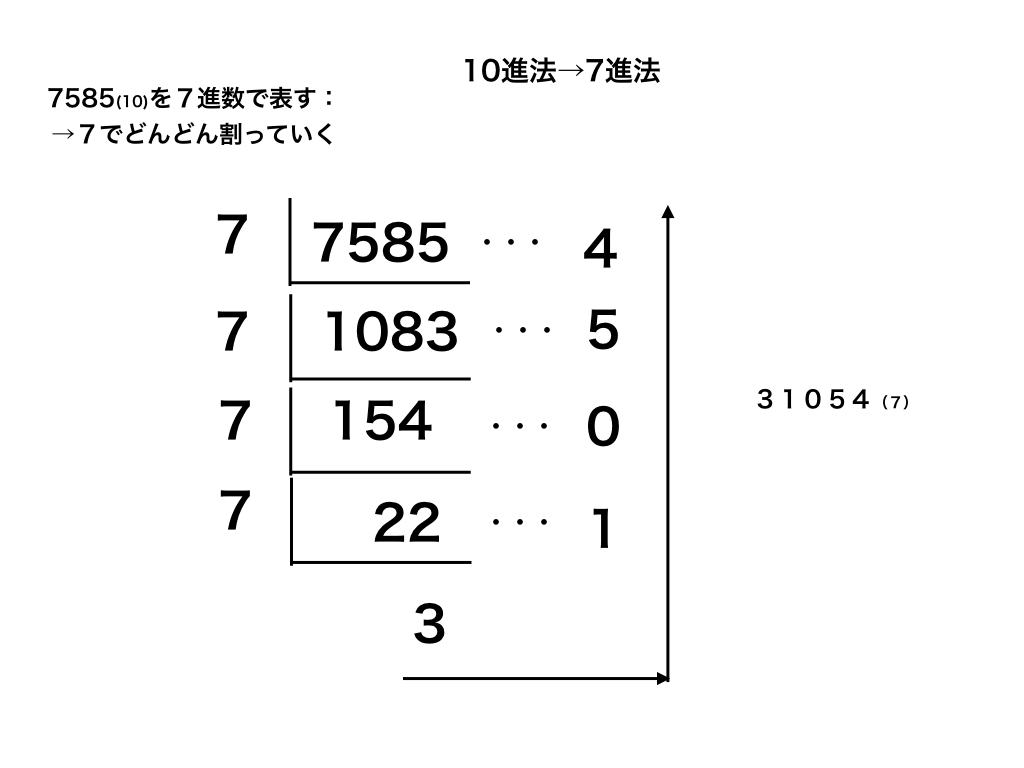
<図1:10進数で表された数をn進数に変える方法図>
次にn進法→10進法表示の逆である、10進法→n進法の変換の仕方を解説していきます。
$$<図1>に先ほどの7585_{10}を7進法に戻す方法を示しました。$$
(ここでは7進法にする方法を説明しますが、その他のn進法にしたい場合には、文章の7をnに読み替えて下さい。)
具体的なやり方は、7585(10)をn=7でどんどん割っていきます。
7585÷ 7=1083 余り4 ここで余りを右に書いて置きます。
1083÷ 7 =154 余り 5
154÷ 7 =22 余り0 割り切れる(余りが0)の時も右に0と書きます。
22÷ 7 =3 余り 1。
3は7より小さくこれ以上は割れないのでここでstopします。
そして、最後に残った「3」→余り「1」→一つ前の余り「0」→一つ前の余り「5」
→最初の割り算の余り「4」の順番に辿っていくと、
31054となり、たしかに元の7進法表示と一致します!
n進法での四則演算
n進法での四則演算(足し算/引き算/掛け算/割り算)の仕方は2通りあり、
・一旦10進法にして計算してからn進法に戻す方法
・n進法のまま筆算で解いてしまう方法
があります。当然後者の方が慣れれば早く処理できるのですが、
それまではミスをしやすいというデメリットもあります。
また、割り算だけは特にn進法での筆算がやりにくいので、
前者の10進法を経由する方が良いことも多いです。
n進法の足し算
$$(例1)102_{3}+201_{3}=?$$
3進法で表された数どうしの足し算を例にします。ここでは十進法を経由せず直接計算していきます。
計算(筆算)の方法
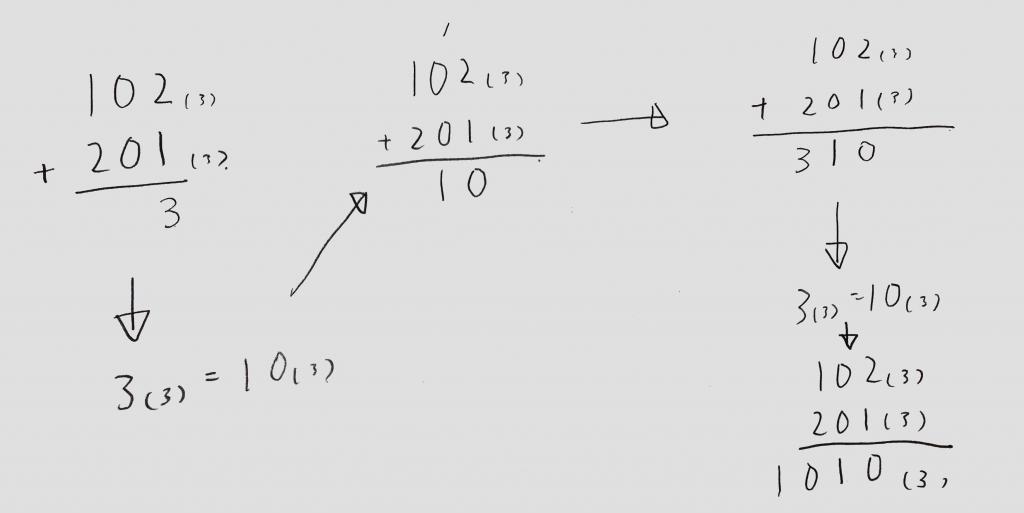
<図2:n進法のまま筆算で足し算をする方法>
<図2>を見ながら読んでいって下さい。
まず普通の足し算と同じ様に1桁目から足していきます。
2+1=3 ここで3進法は「0、1、2」で表し3になると繰り上げる決まりだったので、
1桁目は0、二桁目に1が繰り上がります。
次に2桁目の数字を足していきます。先ほど繰り上がった、1+0+0=1より二桁目は1になります。
最後に3桁目1+2=3となり、1桁目と同様に繰り上がり3桁目は0、4桁目が1となり計算終了です。
よって、$$102_{3}+201_{3}=1010_{3}$$
基本的に何進法でも解き方は同じです。
n進法の引き算
引き算もn進法のまま行います。足し算と同じく筆算して行けば良いのですが、
注意する点は、引かれる数より引く数が大きい場合です。
10進法では、一つ上の桁から「借りてきて」計算をします。
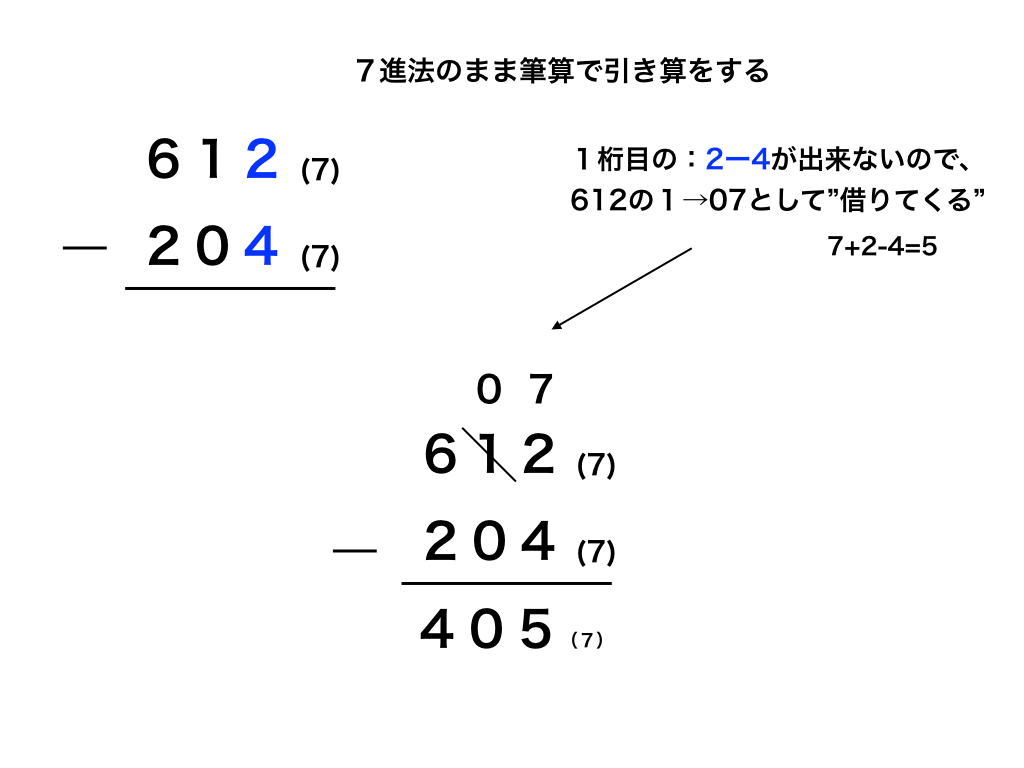
<図3:n進数の引き算を筆算で行う方法>
同様に<図3>と共に解説していきます。
$$612_{7}-204_{7}$$
今回は5進法の引き算です。
はじめに2-4が出来ないので、
$$10進法の時と同じく2桁目の1_{7}から「7」を借りてきます。$$
以降は普通に筆算すれば問題ありません。
$$612_{7}-204_{7}=405_{7}$$
n進法の掛け算
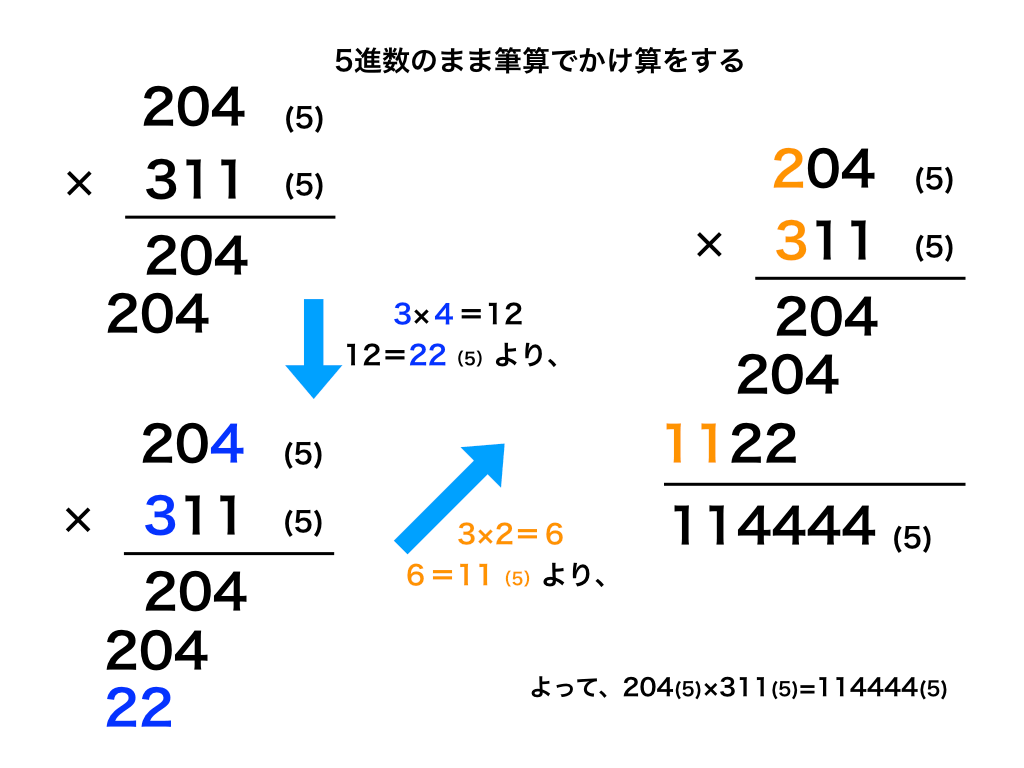
<図4:n進法での掛け算>
<図4>の様に、掛け算は少しだけ複雑です。
$$204_{5}× 311_{5}=$$
$$204_{5}× 11_{5} は問題無いと思います。ただこれまでの筆算と同じです。$$
$$204_{5}× 300_{5}が少し分かりにくいです$$
まず、3× 4=12 ですが、5進法の掛け算なので
$$12=22_{5}に変換して書き足します。$$
3× 0=0よりこの桁は飛ばして、
$$3× 2=6、 6を5進法に変換して、11_{5}$$
$$従って、204_{5}× 300_{5}=112200_{5}$$
$$全て合わせると、204_{5}× 311_{5}=$$
$$204_{5}+2040_{5}+112200_{5}となり、$$
$$204_{5}× 300_{5}=114444_{5}が答えです。$$
n進法の割り算
割り算は、一旦十進法を経由して行う方をお勧めします。
なぜなら、先程にも書いた様に時間的にも計算ミスの危険性でも、
あえてn進法同士の筆算をするメリットがあまり無いためです。
$$240_{8}÷ 4_{8}=?$$
一旦8進法表示から10進法表示に変換します。
変換方法は上のn進法→10進法で紹介した通りです。
$$0× 8^{0} + 4× 8^{1}+2×8^{2}$$
$$=0+32+128=160_{10}$$
$$4_{8}=4× 8^{0} =4_{10}$$
$$従って、160_{10}÷ 4_{10}=40$$
よって、40を8進法に戻せば終了です。
<図1>の10進法→n進法の作業をして(n=8)
$$40_{10}=50_{8}なので$$
$$240_{8}\div 4_{8}=50_{8}が答えになります。$$
慣れてくるとスピードアップするので、ここまで丁寧に書く必要は無くなります。
まとめとn進数シリーズ一覧+ SPI対策
さて、今回は基礎的なn進法と10進法の変換+四則演算の仕方を解説しました。
苦手意識を持つ人が多い分、何度か復習して自由自在にn進法を操れる様になると差をつけやすい分野です。
以下にこの記事の応用問題や、頻出の融合問題を解説したシリーズを作成したので、ぜひ続けてご覧ください!
第一回:「今ここです」
第二回:「n進数の一般化とその応用問題の解き方」
第三回:「n進数と桁数・不等式との応用問題」(NEW!)
お疲れさまでした。
今回も最後までご覧いただき、有難うございました。
お役に立ちましたら、シェア&当サイト公式Twitter(@linkyjuku_tweet)のフォローをお願いします!
記事についての質問や、誤植、その他のお問い合わせはコメント欄までお願いします。

