ジョルダン標準形の意味・目的と作り方
<この記事の内容>:線形代数の中でも苦手な人が多く、一つの到達点でもある『ジョルダン細胞・ジョルダン標準形』の目的・作り方を解説していきます。
ここまでの線形代数の知識は「線形代数の入門シリーズ:解説記事一覧」←よりご覧ください。
目次(タップした所へ飛びます)
ジョルダン標準形とは
以前、「固有値と固有ベクトルを使って対角化を行う方法」を紹介しました。
この対角化は”一部の条件を満たした正方行列”に対してしか利用できません。
そこで、対角行列に”似せた”『ジョルダン標準形』を代わりに作ろう!ということが今回のテーマです。
対角行列との比較
対角行列:『一部の正方行列』のみに対して、対角成分のみに固有値λiが並び、それ以外の成分はすべて0の行列。
ジョルダン標準形:『基本的に全ての正方行列』の対角成分に以下で解説する『ジョルダン細胞』が並んだ行列で、それ以外の成分が0の行列。
ジョルダン細胞とは
対角成分がλ、かつその上の部分が”1”のような正方行列を『ジョルダン細胞』と言います。
(例:3次のジョルダン細胞)
\(\begin{pmatrix}
\lambda & 1 & 0 \\
0 & \lambda & 1 \\
0 & 0 & \lambda
\end{pmatrix}\)
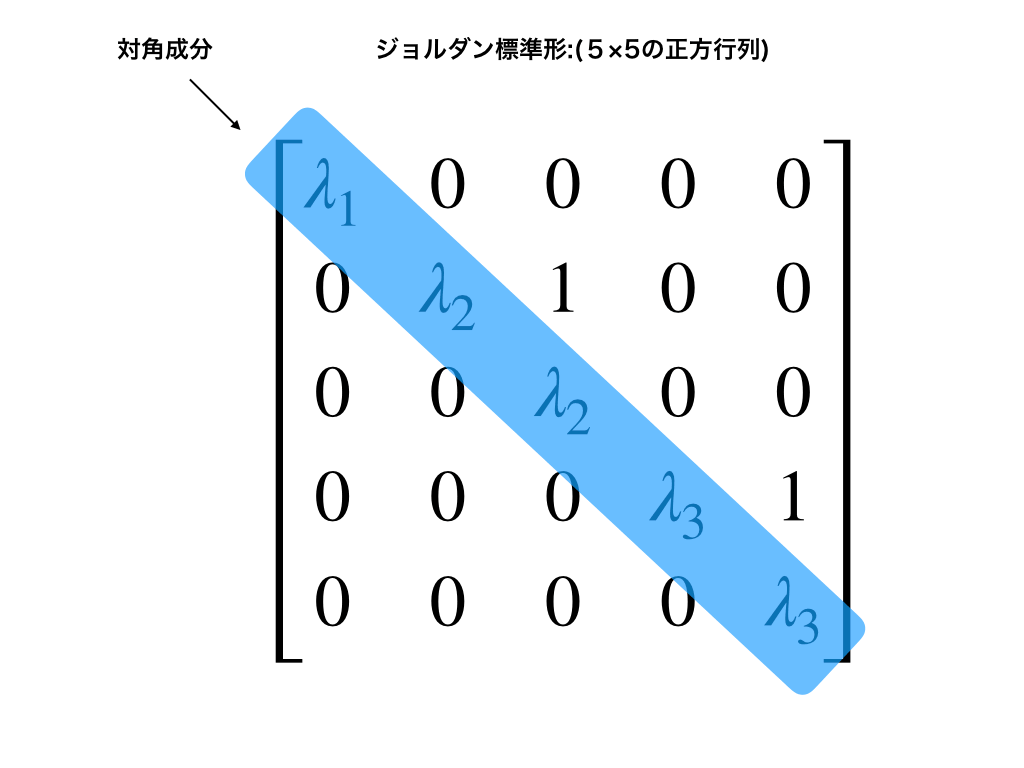
この様なジョルダン細胞を対角成分に並べた「ジョルダン標準形」の例が↓です。
\(\begin{pmatrix}
\lambda 1 & 0 & 0 & 0 & 0 \\
0 & \lambda _{2} & 1 & 0 & 0 \\
0 & 0 & \lambda _{2} & 0 & 0 \\
0 & 0 & 0 & \lambda _{3} & 1 \\
0 & 0 & 0 & 0 & \lambda _{3}
\end{pmatrix}\)
<ジョルダン標準形中のジョルダン細胞の例>
ジョルダン標準形とその対角線上のジョルダン細胞
人間の体が細胞から成るように、『ジョルダン標準形』もジョルダン細胞で構成されます。
先ほどの5次のジョルダン標準形を固有値λと“1”に注目して見てみると、以下の様に3つのジョルダン細胞で出来ている事が分かります。
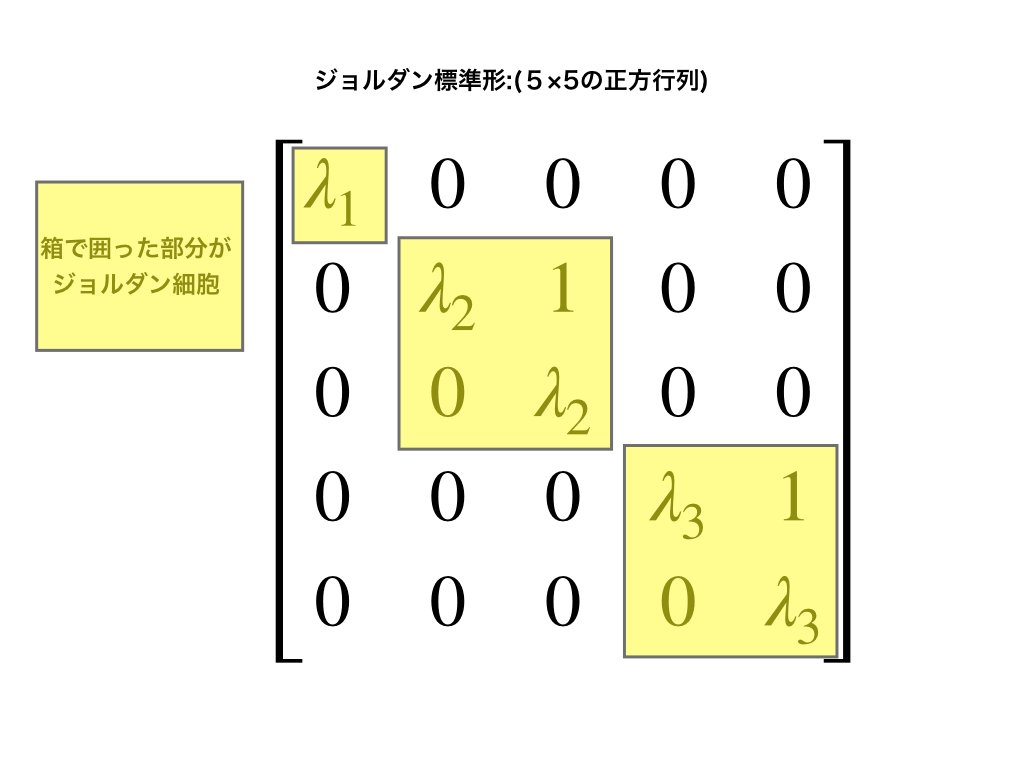
<ジョルダン標準形の中にあるジョルダン細胞>
ジョルダン標準形の作り方・手順
ではここからは実際にn次正方行列(=Aとする)をジョルダン標準形に変形していきます。
かなりややこしく、計算ミスを起こしやすいですがここをクリアすれば線形代数はokになります。
基本的な流れは、
『固有方程式を解く』
→『固有値λが求まる』(※:ここでλが重解や三重解を持つ)
→『λに対応する固有ベクトル+(λがたりないので、左で作った固有ベクトルを利用して)残りのベクトルを作る』
→『上のベクトルから変換行列Pを作る』
→『Pの逆行列とPでAを挟む』
→『J:ジョルダン標準形が求まる』
この流れを(★)とします。
2次の場合
まず、行列Aの固有値・固有ベクトルを求めるときと同様に、Ax=λxを移行してxでくくり(A-λI)x=0。さらに、\(固有方程式\varphi_{a}=0\)を解いて固有値を求めます。
実際に手順を見た方が理解しやすいので、次の行列Aをジョルダン標準形にしていきます。
具体例
$$A=\begin{pmatrix}
1 & -2 \\
2 & 5
\end{pmatrix}$$
まず、\(\det (A-\lambda I )=0\)を求めます。
$$(※):\begin{pmatrix}
1-\lambda & -2 \\
2 & 5-\lambda
\end{pmatrix}=(1-\lambda)(5-\lambda)-(-4)$$
\(=(\lambda-3)^{2}より、λ=3(重解)\)
重解になった時点で、「固有値と固有ベクトルを使った対角化」ができない事がわかります。
そこで、ジョルダン標準形を目指し、(※)のλに3を代入した行列(これをBとします)を作り、Bx=0の形に持っていきます。
\(\begin{pmatrix}
-2 & -2 \\
2 & 2
\end{pmatrix}\vec{x}=\vec{0}\)
\(\vec{x}=\begin{pmatrix}
x_{1} \\
x_{2}
\end{pmatrix}\)とすると、\(-2x_{1}-2x_{2}=0,すなわちx_{1}=-x_{2}\)となるため、適当な値を代入します。
ここでは、\(x_{1}=2\)とします。・・・(※※)
本来ならば、ここでもう一個の固有値を(※)のλに代入して二つ目のベクトルを作りたいのですが、λが重解なので上手くいきません。
そこで、次は以下のような工夫をする事でもう一つの列ベクトルを求めます。
\(\begin{pmatrix}
-2 & -2 \\
2 & 2
\end{pmatrix}\begin{pmatrix}
x_{3} \\
x_{4}
\end{pmatrix}=\begin{pmatrix}
x_{1} \\
x_{2}
\end{pmatrix}(Bx'=x)\)
つまり(※※)で作った列ベクトルを右辺に持ってきて、左辺には行列Bと成分が不明の列ベクトルを持ってきます。
この計算を行う事で、変換行列が求まります。
\(\begin{pmatrix}
-2 & -2 \\
2 & 2
\end{pmatrix}\begin{pmatrix}
x_{3} \\
x_{4}
\end{pmatrix}=\begin{pmatrix}
2 \\
-2
\end{pmatrix}\)
より、\(-2x_{3}-2x_{4}=2⇔x_{3}+x_{4}=-1\)
ここで、\(x_{3}=1とするとx_{4}=-2\)
\(変換行列P=\begin{bmatrix}
x_{1} & x_{3} \\
x_{2} & x_{4}
\end{bmatrix}=\begin{bmatrix}
2 & 1 \\
-2 & -2
\end{bmatrix}\)
ジョルダン標準形は$$P^{-1}AP=-\frac {1}{2}\begin{pmatrix}
-2 & -1 \\
2 & 2
\end{pmatrix}\begin{pmatrix}
1 & -2 \\
2 & 5
\end{pmatrix}\begin{pmatrix}
2 & 1 \\
-2 & -2
\end{pmatrix}$$
を計算すると求まるので、(逆行列の求め方は「逆行列を求める公式とガウスの消去法」を参考にしてください。)
$$P^{-1}AP=-\frac {1}{2}\begin{pmatrix}
-4 & -1 \\
6 & 6
\end{pmatrix}\begin{pmatrix}
1 & -2 \\
2 & 5
\end{pmatrix}$$
$$=-\frac {1}{2}\begin{pmatrix}
-6 & -2 \\
0 & -6
\end{pmatrix}$$
$$よって、P^{-1}AP=\begin{pmatrix}
3 & 1 \\
0 & 3
\end{pmatrix}$$
ここで、求めた行列を見ると確かに対角成分が先ほど求めた固有値λ=3になっており、1は3の上のみに存在する”ジョルダン標準形”の形である事が確認できます。
なお、途中のベクトルを求める際、
\(\vec{x}=\begin{pmatrix}
x_{1or3} \\
x_{2or4}
\end{pmatrix}\)
の\(x_{1,2,3,4}\)に代入した値は条件(\(x_{1}=-x_{2}\)など)さえ満たせばどの数字を使っても問題ありません。
3次のジョルダン標準形(追記中)
上の項では2次の正方行列を扱いましたが、今度は3次(3×3)の場合です。
2次の場合に比べても計算量が増えるだけでなく、固有値の重解の個数が
・(1つの重解とそれ以外のもう1つの解)
or
・(解が一つのみ:つまり3重解)
の2通りあり、ジョルダン細胞の位置の違いなどでタイプが複数あります。
4次以降はさらに大変です。。
ただし、3次の場合は基本的に2次の時と解法(★)は同様なので、教科書等の解説もスッと入ってくるはずです。(本記事でも追記予定です。)
なお、3次の固有方程式を解く際には、「サラスの公式で3×3行列の行列式を求める」を使うので、曖昧になってしまっている人は復習しておきましょう。
ジョルダン標準形まとめ
・対角化不可能な正方行列に対して”代替”として『ジョルダン標準形』を作る。
・ジョルダン細胞が対角成分の上に並ぶ行列が『ジョルダン標準形』である。
・(★)の流れにあるように、固有値が重複した際の「列ベクトルの作成→変換行列」をよく復習しておく。
・関連するものとして『固有値分解』・『特異値分解』などがあり、それぞれの記事で解説していきます。
線形代数の関連記事一覧
>>「線形代数の解説記事総まとめ」<<
今回も最後までご覧頂き、有難うございました。
当サイト「スマナビング!」では、読者の皆さんのご感想をコメント欄にて募集しております。
また、 B!やシェア、Twitterのフォローをしていただけると、励みになります。
・その他のお問い合わせ/ご依頼に関しましては、運営元ページからご連絡下さい。

