2つの円の位置関係と共通接線の求め方：図形と方程式(2)

2019-06-14 2020-03-21

執筆者・編集者プロフィール

安田周平

■個別指導塾YES/YESオンラインスクール塾長・船場物産株式会社代表取締役社長。
★塾長及びyesの講師陣がマンツーマンで英検・TOEIC・TOEFL・数検・大学入試対策(英・数・物・化・情報1)を指導します。(東京・大阪・オンライン)
★詳細は以下のリンクよりお問い合わせください。
■『スマナビング！を見て受講希望』とお伝えいただければ、特別優待を準備しています。

＞＞個別指導塾YES公式HP＜＜

図形と方程式シリーズ２：円（応用問題編）

＜この記事の内容＞：「円の方程式と弦の長さ（図形と方程式１）」に引き続き、円の応用問題についてそれぞれ詳しく解説していきます。

目次(タップした所へ飛びます)

2つの円の位置関係
- 円の中心間距離の求め方
- 半径と中心間距離で位置関係を分類
共通接線：2種類4つ
図形と方程式：円のまとめと次回へ
- 関連記事一覧

2つの円の位置関係

今回のメインテーマは「円が2つ存在するとき」どのような問題が出題されるかです。

まずはじめに、2つの円の関係（位置・距離・内接外接など）を調べる方法と、それぞれのイメージ図を紹介していきます。

円の中心間距離の求め方

まずはじめに行うのが、円の中心点からもう一方の円の中心点までの距離を調べ、その距離と２円の半径の関係を比べることです。

具体的には、2つの円の中心点の座標から三平方の定理を使って中心点どうしの距離を求めます。

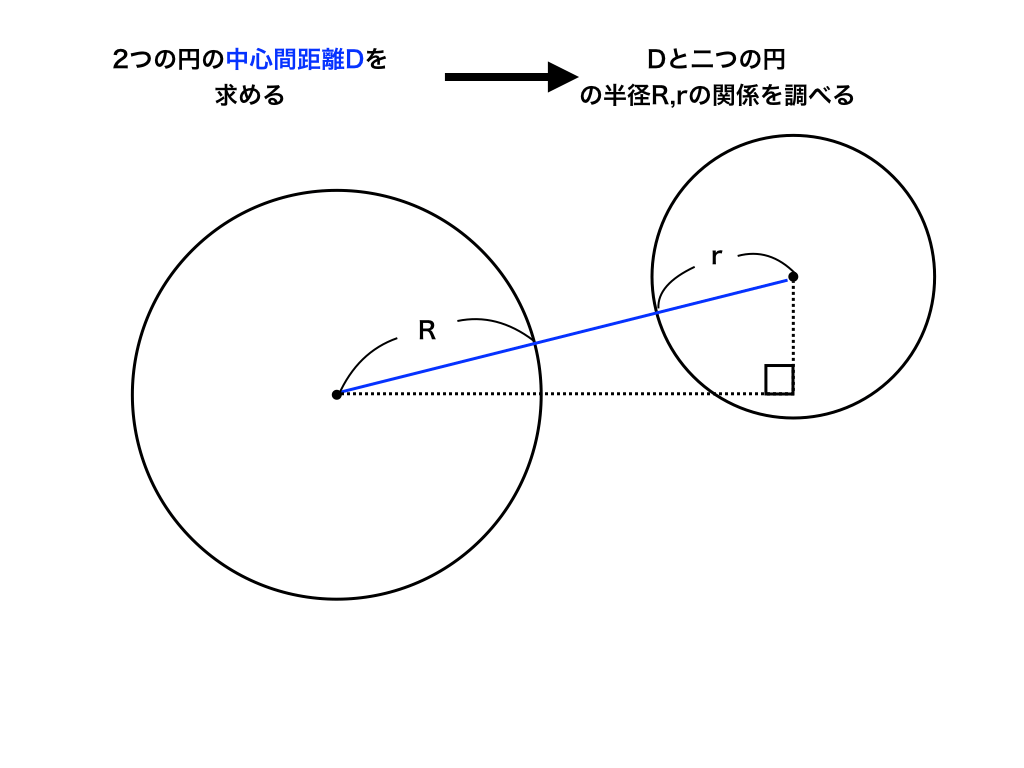
＜三平方の定理でDを求める＞

半径と中心間距離で位置関係を分類

上で求めた中心点どうしの距離$ここではDとします$と円の2つの半径$同様にR,rとします$を利用して、5つのタイプに分類していきます。

２つの円の中心間距離が半径の和より大きい場合：D>R+r

D>R+r、すなわち半径を足し合わせてもDに届かない場合は円は離れている状態です。

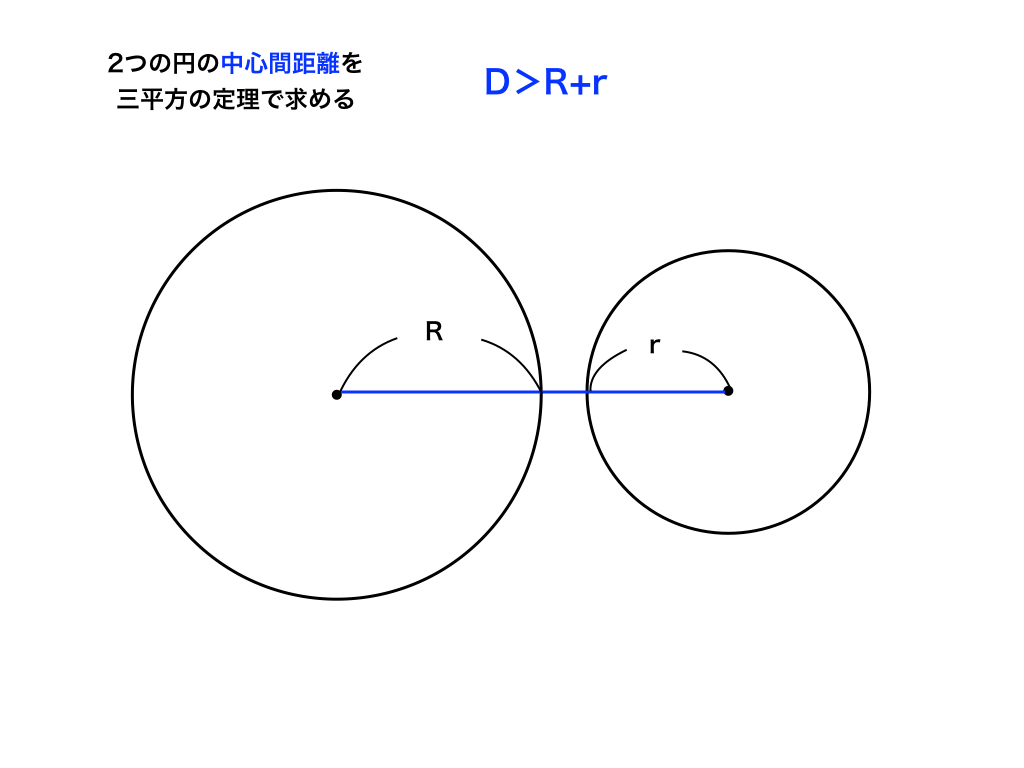
＜D>R+rの時＞

2つの円が外接する場合：D=R+r

このタイプは重要です。以下の図でもわかるように「半径を足し合わせた距離が中心間距離と等しい」場合外接します。

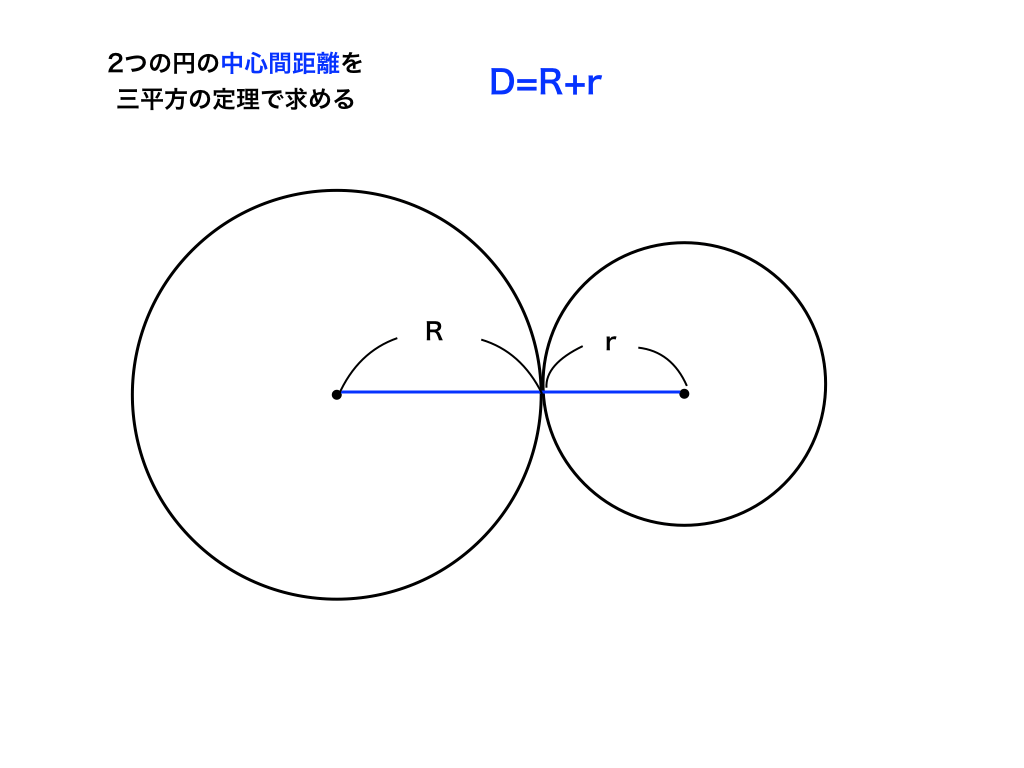
＜D=R+r（外接の場合）＞

２点で交わる(交点を持つ)場合：|Rーr|＜D＜R+r

この半径の差＜中心間距離＜半径の和となるタイプは、次回「(作成中)円の発展編：”束”と２交点を通る直線の式」で詳しく扱いますが、2つ交点を持つ＝円が交わっている状態になります。

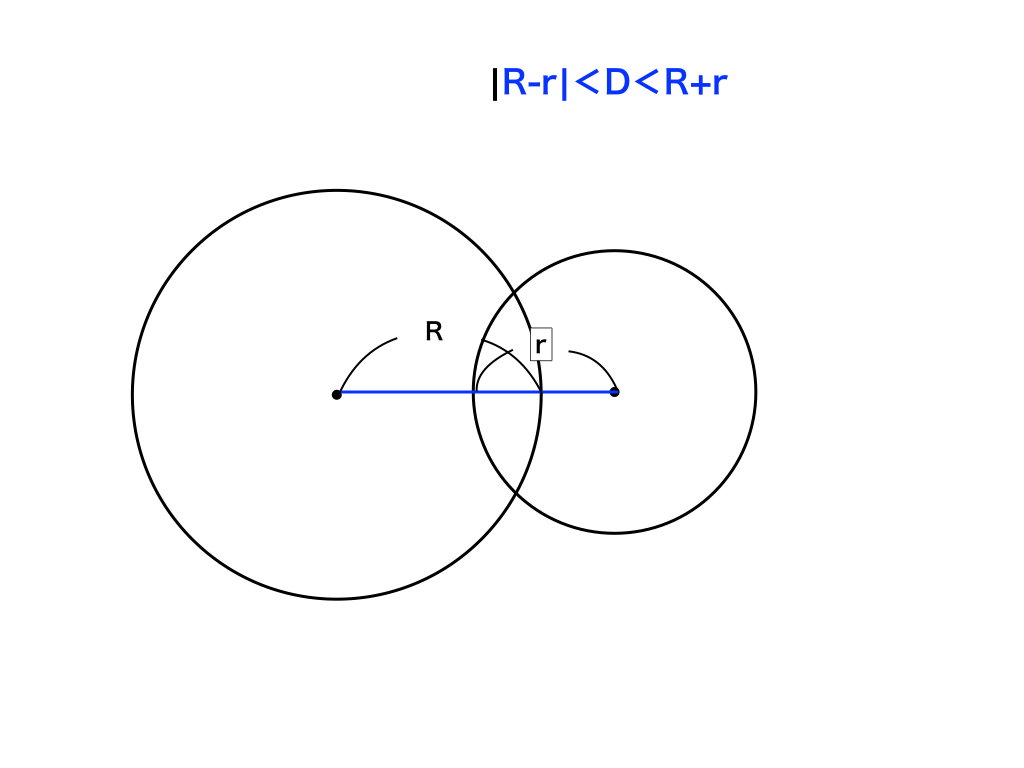
＜２交点を持つ場合＞

2つの円が内接する場合：D=R-r

先ほどの外接の時とは反対に、D=|R-r|ならば内接します。

また、半径の差よりも中心点間の距離が小さい場合は、半径が大きい方の円の中にもう一方の円が存在する状態となります。

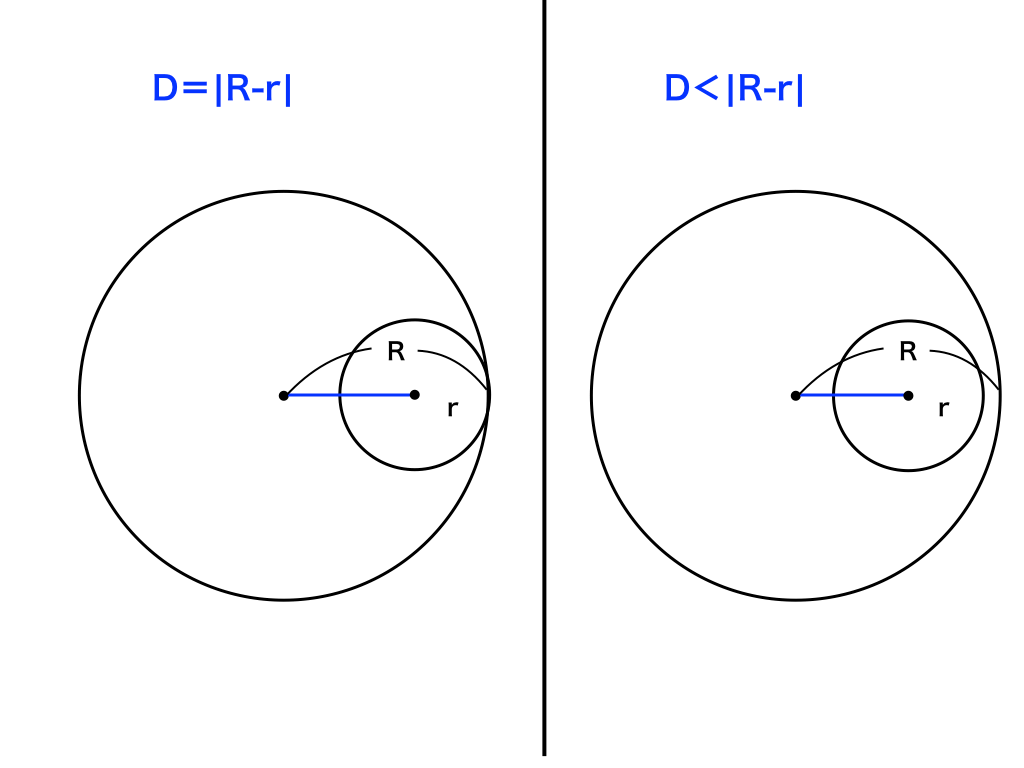
＜内接（左）と半径Rの円内にもう一方の円が入る場合(左)＞

共通接線：2種類4つ

応用問題編２は、円の接線についてです。

特に、2つの円のうち1つの円の接線がもう一方の円に接するといういわゆる”共通接線”の問題について具体的な問題を通して解法を習得していきます。

共通接線

以下の図のように円が2つになると、その両方に接する直線は４本存在することがあります。

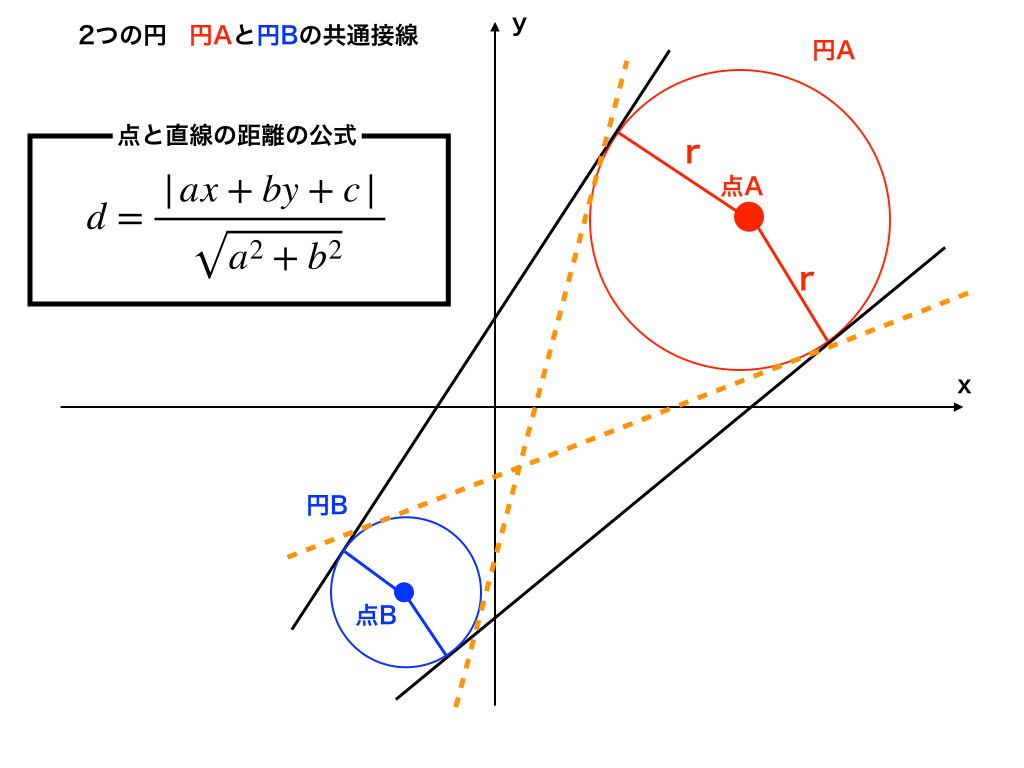
＜２円の共通接線＞

接線の求め方（復習）

円の接線はその円(中心が$\alpha,\beta$\),$半径r$とし、接点が分かっている＝$s,t$とする時、$(x-\alpha)s+(y-\beta)t=r^{2}$で表すことができます。

共通接線4つの具体的な求め方

基本的な解き方は、

手順１：まずどちらかの円（計算が楽な方を選ぶと効率よく進められます）上の、接点の座標を点A(a,b)のように仮定し、接線の公式を使って接線の方程式（式１とする）を作ります。

手順２：”点と直線の距離”の公式、および、もう一方の円（円２とする）の中心点の座標より、手順１で作った接線の式（式１）との距離を調べます。

手順３；手順２で求めた距離が円２の半径と等しくなる時、（式１）は円２、円１両方に接する”共通接線”であることから、$(a,b)$を計算し(式１)に代入することで(式１)が求まります。

共通接線の確認問題

実際に確認問題を解いて解法を定着させておきましょう。

問）いま、x-y座標平面上に$x^{2}+y^{2}=1$で表される円1と、$x^{2}+(y-4)^{2}=4$で表すことが出来る円2が存在する。この時、円１と円２両方に接する直線（接線）の式を求めよ。

解答解説）

今回は円1上の点Aを接点とし、その座標を(a,b)と置くこととします。

接線の公式より、その式は$ax+by=1$・・・(1)

また、点Aは円1上の点であることより$a^{2}+b^{2}=1$・・・(2)が言えます。

$ax+by-1=0$と円2の中心(0,4)との距離が$\sqrt{4}=2$であれば良いので、

点と線の距離の公式：$$\frac{|ax+by+c|}{\sqrt{a^{2}+b^{2}}}$$を使って、

$$\frac{|4b-1|}{\sqrt{a^{2}+b^{2}}}=2$$

ここで$a^{2}+b^{2}=1$・・・(2)と$\frac{|4b-1|}{\sqrt{a^{2}+b^{2}}}=2$より、$|4b-1|=2,4b-1=\pm 2$、（絶対値については「絶対値の意味と問題の解法」を参考にしてください。）

これを解くと、$b=\frac{3}{4},\frac{1}{4}・・・が求まります。$

$a^{2}+b^{2}=1$・・・(2)とbの値より、

・$b=\frac{1}{4}の時、a=\pm \frac{\sqrt{15}}{4}$

・$b=\frac{3}{4}の時、a=\pm \frac{\sqrt{7}}{4}$

以上より、円1と円2の共通接線は

$$\pm \sqrt{15}x+y-4=0 ,\pm \sqrt{7}x+3y-4=0$$

・・・（答）となります。

図形と方程式：円のまとめと次回へ

今回は、2つの円に関連する2つの頻出問題を取り上げました。

前回の基礎的な内容や（すでに学習済みの人は）ベクトル方程式、複素数平面での円などとともによく復習しておきましょう。

次回は、2つの交点を通る直線の式を求める問題と束・恒等式といった円の発展問題を解説します。