
浮力とは? 浮力の基礎と単振動の問題
<この記事の内容>:「船が浮いたり、お風呂に入ると体が軽くなったりする」。みなさんも身近に感じるそんな現象を“浮力”と言います。
物理でも浮力を苦手な人が多く、さらに単振動などとの融合問題になるとお手上げな方もいるのではないでしょうか?
この記事では、「不思議な浮力の仕組み」を詳しく解説して浮力の基礎をマスターしたのち、単振動との応用問題をカンタンに解く方法を紹介しています。
(単振動が苦手な人へ:0から解説した記事を途中で用意しているので、それを読んで貰えば今回の融合問題も解けるようになります。)
目次(タップした所へ飛びます)
浮力とは
浮力を理解するのには、まず水圧を理解しなければなりません。順を追って解説していきます。
水圧の特徴
水圧とは読んで字のごとく水の重さによって発生する圧力のことです。水圧の特徴は主に2つあります。
1) 深くなればなるほど水圧は大きくなる
→水圧の要因は、水中の物体よりも上にある水の重さです。
したがって深くなればなるほど、物体の上にくる水量は多くなります。ゆえに、水圧は深くなればなるほど大きくなります。
2) 水圧は四方八方から受ける
→物体というのは常に安定を求めています。少し哲学的なことに聞こえるかもしれませんが、地球が自転しているのも、太陽が熱を放出しているのもそうです。
そして液体(液体を構成する分子)もポジションを安定させるために、四方八方に力を与えているのです。
ですから水中の物体は四方八方から圧力を受けるのです!
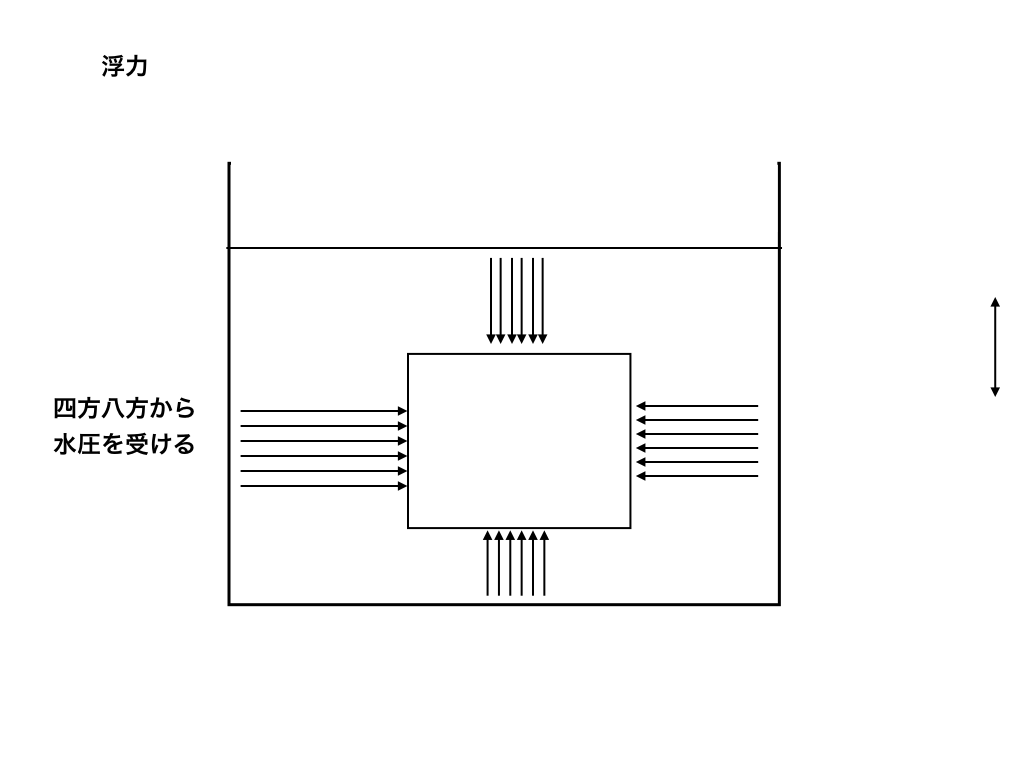
浮力
水圧の特徴を2つ解説しましたが、実はこれらの要素が浮力を説明しています。
『浮力とは、水圧の特徴から、水中の物体の上面を押す力より下面を押す力が大きいことにより発生する鉛直上向きの力のこと』
例えば、あなたが満員電車にいて他の乗客より体格が小さいとしましょう。
この時、電車が揺れる(周囲から圧力を受ける)と体はどんどん浮き上がってきますよね?これが浮力なのです。
簡単な説明ですが、浮力の基本的な意味は理解できたかと思います。ここからは実際に物理の計算で使う“公式”などを紹介していきます。
浮力の公式
F:浮力
\(F = \rho Vg\) 、
\(\rho\) : 周りの流体の密度 ,V : 物体が沈んでいる体積 ,g : 重力加速度
密度は、一般的に\(\rho\) (ローと読みます)で表します。
この浮力の原理は紀元前250年頃、アルキメデスが王冠の金の純度を調べる時に発見しました。(ちなみにその時日本は土器を作っています...)
この時のエピソードは有名なので、また紹介したいと思います。
浮力は物体が排除した(押しのけた)流体(液体)の重さに等しいので、浮力は物体の質量とは無関係になります。
ですから浮力を満員電車に例えた時、体格が小さいという設定をしたのです!
やはり文字や数字だけで解説すると、少しわかりにくくなるので、実際に問題を解きながら理解を深めます。
ここでは、頻出の単振動と浮力の融合問題を見ていきます。
<浮力と単振動の融合>
融合問題:底面積S、高さh、密度\(\rho\)の円柱形をした一様な物体を、
密度\(\rho _{0}\)の流れのない一様な液体中に沈ませた。
この時、重力加速度の大きさをgとする。
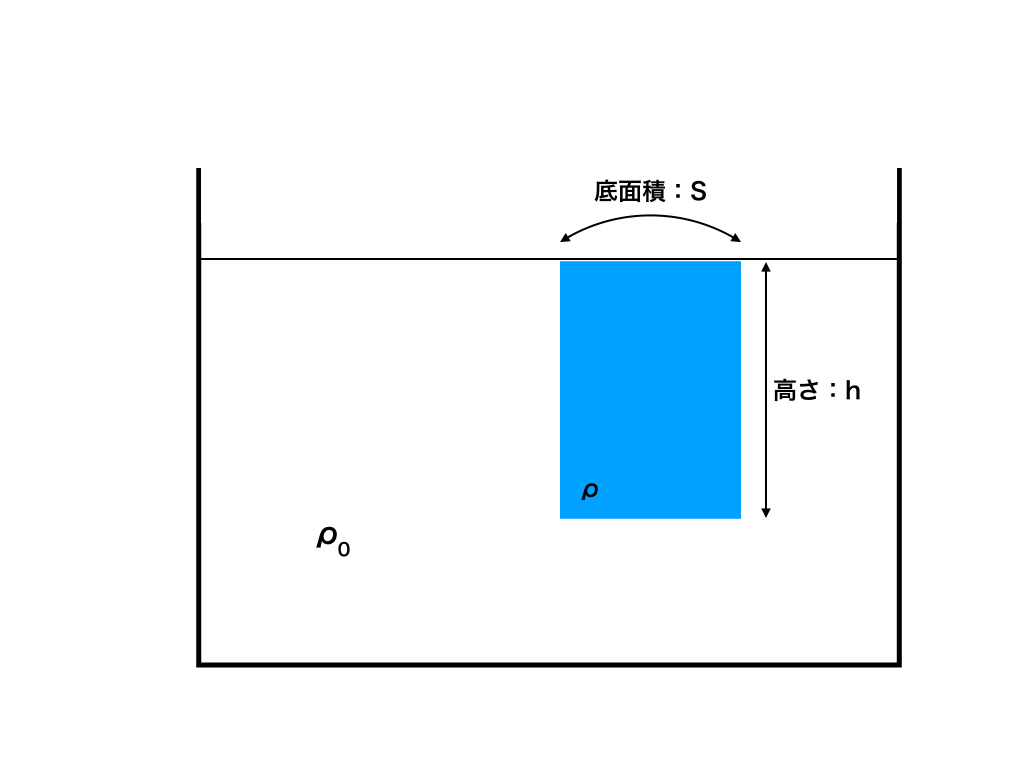
<問題図1>
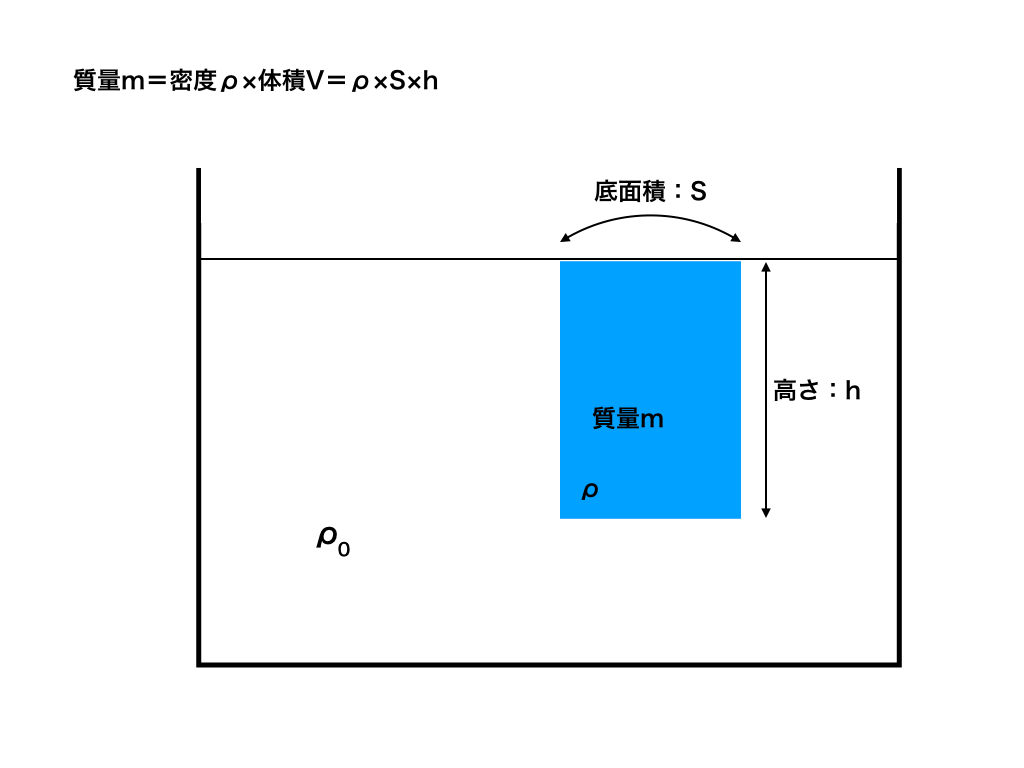
物体の質量を求める:密度の式
(A1)物体の質量mはいくらか?
$$m =\rho v =\rho sh[kg] ←\rho =\frac{m}{v}$$
の密度の公式を使えば一発で解けます!
浮力と重力の釣り合い
(2):\(\rho = \rho _{0}\)の時、物体にはたらく浮力は重力とつり合う。
このことから、物体が液体中に完全に没している時の浮力(F)の大きさを求めよ。
力のつり合いを書いて、
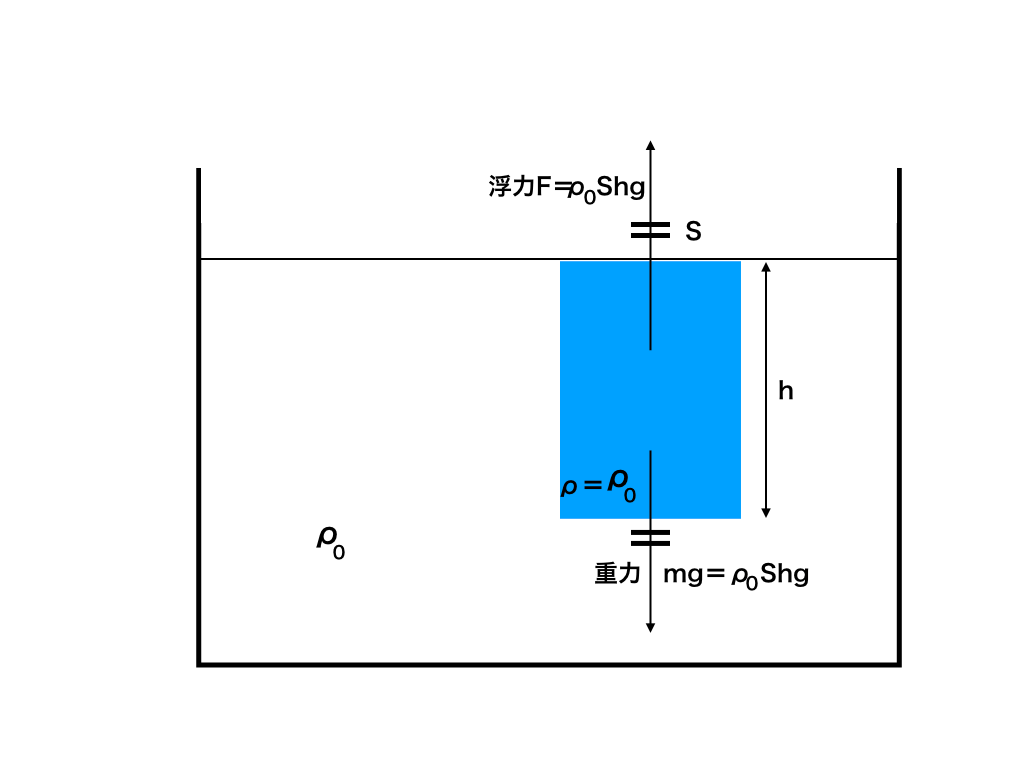
\(F = \rho _{0} s\times h\times g [N] \)←前述した、浮力の公式を利用しただけです。
一部が沈んだ物体と浮力
(3)物体は液面に浮上し、下記の図のように底面から長さの部分を液面下にして静止した。
ただし、液面より上の気体の密度は無視してよい
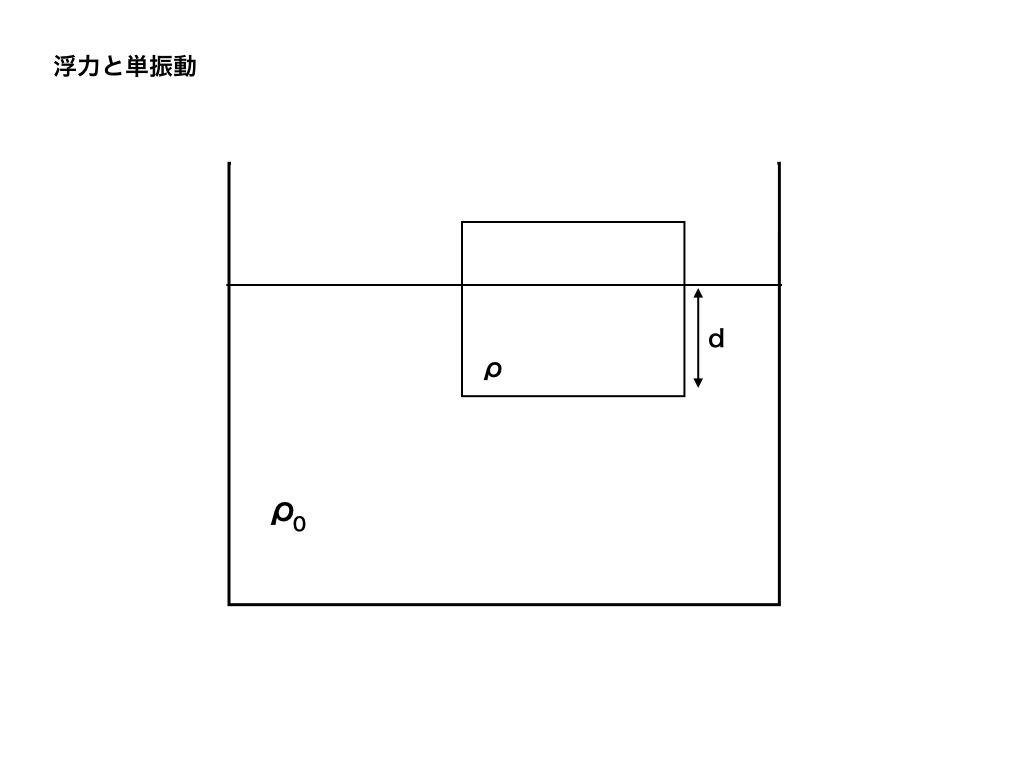
密度ρを求める
ア)物体の密度 \(\rho\)を求めよ
力のつり合いより、物体にかかる力を書き加えて、
\(\rho _{0} \times s\times d\times g =\rho s\cdot h \cdot g\)
よって、
$$ \rho = \rho _{0}\times \frac{d}{h}[kg/㎥]$$
*解説
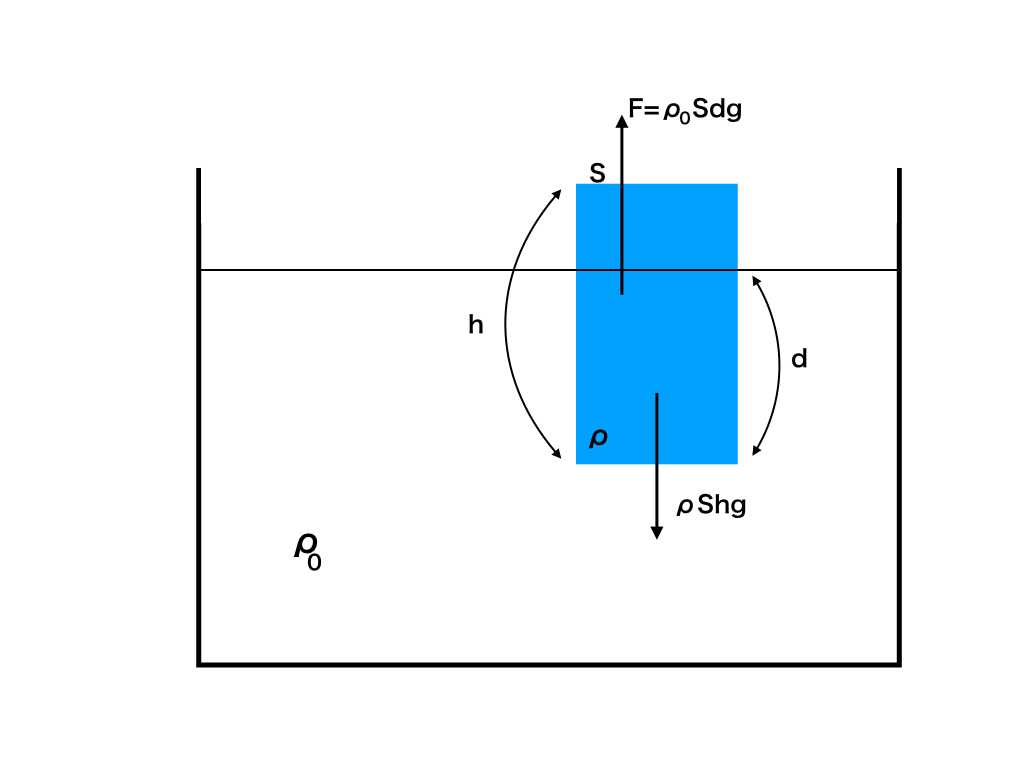
(左辺)は物体にはたらく浮力の式です。ただし、沈んでいる部分が物体全てではないので、沈んでいる部分の体積がsdになります。
一方、(右辺)は重力からくる鉛直下向きの力で、\(mg = \rho shg\) で求めることができます。
問題文にある通り、“静止”しているので(左辺)と(右辺)がイコールになります。後は式を整理するだけです。
外力fを求める
イ) 物体を上から手で押して、上の図の位置からさらに十分小さい距離”δ”だけ沈めた。
この時、手から物体にはたらく力の大きさ(f)を求めよ。
力のつり合いより
\(f +\rho _{0} sdg = \rho _{0} \times s( d +δ)g \)
よって
\(f = \rho _{0}\times sδg\)
*解説
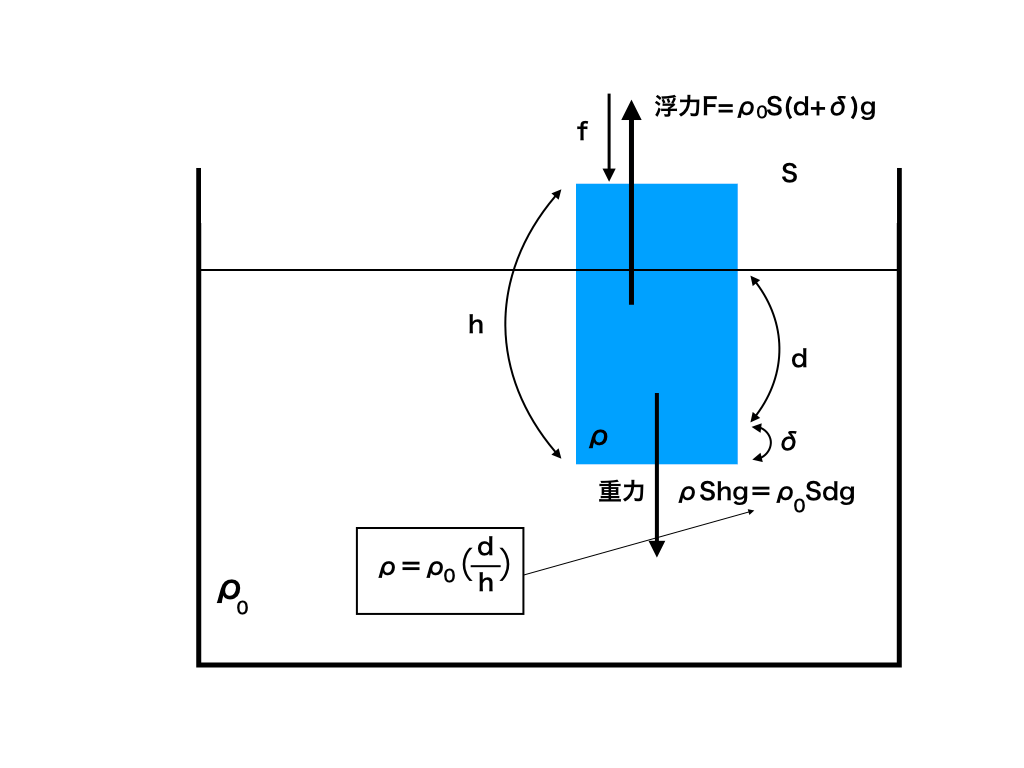
この問題に関しても、慎重に力のつり合いを考えていけば難しくありません。
まず下向きの力は、重力と手で押している分だけ。上向きの力は浮力。
これらの力が加わり静止しているので、同様にイコールで結べば解答に辿り着きます。
式のみでわかりにくいという方は一度図を書いてみましょう。
<ここから単振動の問題に入ります。先に復習しておきたい人、苦手な人は→「これで分かる!1から始める単振動」←をご覧下さい。>
今日の本題:浮力と単振動
ウ) 手を静かに離すと、物体は液面上でz方向に振動した。振動の周期はいくらか。
ただし、液面からの抵抗力などは無視し、円周率はπとする。
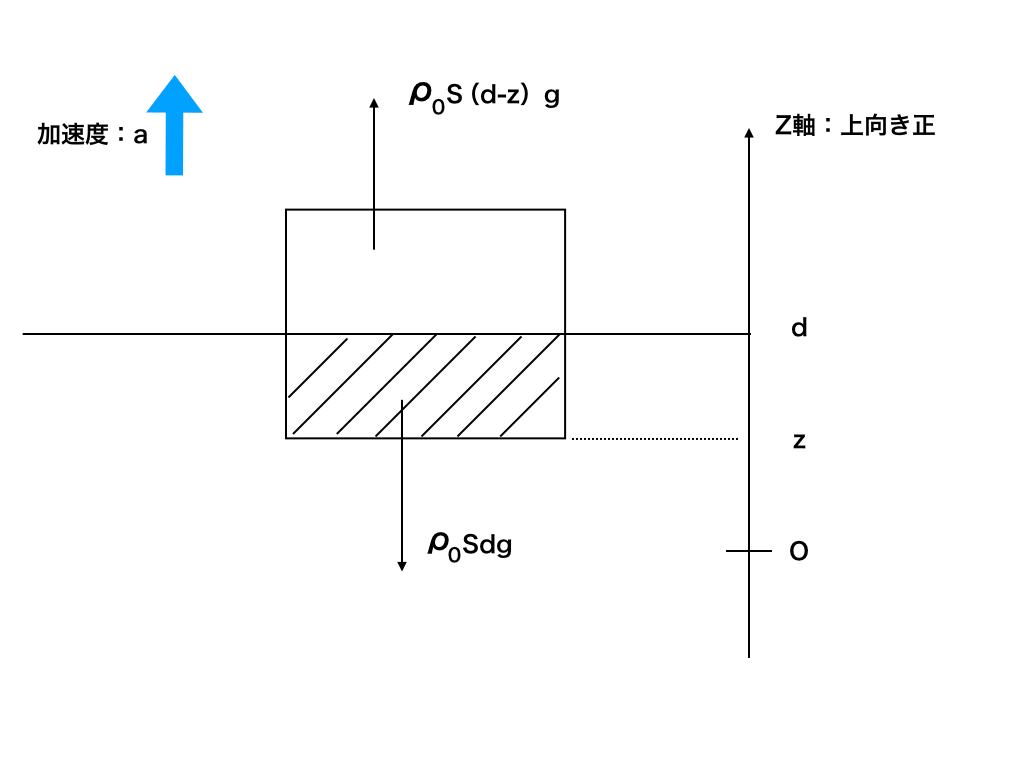
単振動(物理)は軸設定が命でした!今回はうえ向きにz軸正方向を取ります。
液面下d[m]の位置を原点Oとすると、\(\rho _{0}\times sd×a=\rho _{0}\times s(d-z)g-\rho _{0}\times sdg\)
\(\rho _{0} \times sd\times a =-\rho _{0}\times sgz \)
よって$$a = -\frac{gz}{d}$$
単振動の式と比べると、
\(a = -\omega^{2}× zと比べて\)
$$\omega^{2}= \frac{g}{d},\omega > 0 だから \omega =\sqrt {\frac {g}{d}}$$
\(T = \frac{2\pi}{\omega}= 2\pi\sqrt{d/g}[s] ←解答\)
$$T=2\pi \sqrt {\frac {d}{g}}$$
*解説
この問題は力のつり合いと運動方程式がしっかりと理解できているかが鍵になってきます。
ここまでの問題で浮力の解説をしてきましたので、解きにくかったという人はもう一度、運動方程式や力の釣り合いなどを確認すると良いでしょう。
参考記事:「物理基礎の為の三角比・ベクトル(力の釣り合いや力の分解の計算の仕方)」
また、単振動の式にうまく当てはめて、形を意識して解きましょう。
この問題の場合はω^2 = g/dの綺麗な形が出来上がります。
ここまでの内容が理解できていれば、応用問題を解く際も非常に楽に感じられるはずです!
まとめと復習法、単振動の記事一覧
後半は文字が増え少し難解だったかもしれませんが、図を書いて力の分解をしていけば自ずと解答までの道のりが見えてくるはずです。
問題の下に解答がすぐあるという形式ですので、1度目は見ながら、2度目は自分の頭で考えて解くと定着していきます。
それが終わったら、類題にドンドン取り組んでみましょう。
<単振動シリーズの記事>
今回も最後までご覧いただき有難うございました。
このサイトは皆さんの意見や、記事のリクエスト、SNSでの反応などをもとに日々改善・記事追加更新を行なっています。
そこで
・記事リクエストとご意見はコメント欄にお寄せください。
・多くの学生・受験生に利用して頂くために、SNSでシェア(拡散)&当サイト公式Twitterのフォローをして頂くと助かります!
・サイト運営/記事作成の為に是非ご協力お願いします!
・その他のお問い合わせ/ご依頼等は、「運営元ページ」よりお願い致します。

