
沸点上昇と凝固点降下(理論化学/溶液)
突然ですが、あなたは蒸気圧降下と沸点上昇の関係や、凝固点降下が起こる理由を説明できますか?
なんとなく公式にあてはめて計算していると、難易度が上がってきた時に対応できなくなります。
今回は、入試でも「理由」を論述させられることの多く、
苦手な人が多い「溶液」の範囲から「沸点上昇/凝固点降下」について解説していきます。
最新版に更新2019年12月25日。
(前提知識として、「蒸気圧曲線と状態図の見方」にも目を通していおいて下さい。)
目次(タップした所へ飛びます)
蒸気圧降下と沸点上昇
冒頭にも書いた通り、沸点上昇の前にそもそも沸点・沸騰とは何か?を理解していないと公式を覚えるだけになってしまいます。
沸点/沸騰とは何か?
以下のようにQ→A→Q→・・・と書いていきます。試験で理由な意味などを答えさせられる問題(特に記述式の問題)に有効な勉強法です。
A.「沸点」とは「沸騰する温度」のことである。
Q.では沸騰とは何か?
A「沸騰」とは、「飽和蒸気圧と大気圧が等しい時に液体中から蒸発し始める事」である。
Q.飽和蒸気圧とは何か
A.“液体分子が気体中へ飛び出す分子の数”と“気体分子が液体中へ戻ろうとしている分子の数”がちょうど等しい時の圧力のこと。
何となく分かったでしょうか?これまでのQ&Aで分からないところがある人は、
ここから先蒸気圧曲線の知識が必須なので→「状態図と飽和水蒸気圧曲線の見方が分かる!」を読んでおいて下さい。
蒸気圧降下の仕組み
純溶媒に不揮発性である溶質が混ざる事で、<図1>容器の表面にある気体になろうとしている溶媒分子の数が<図2>の純溶媒だけの場合と比べると減ってしまいます。
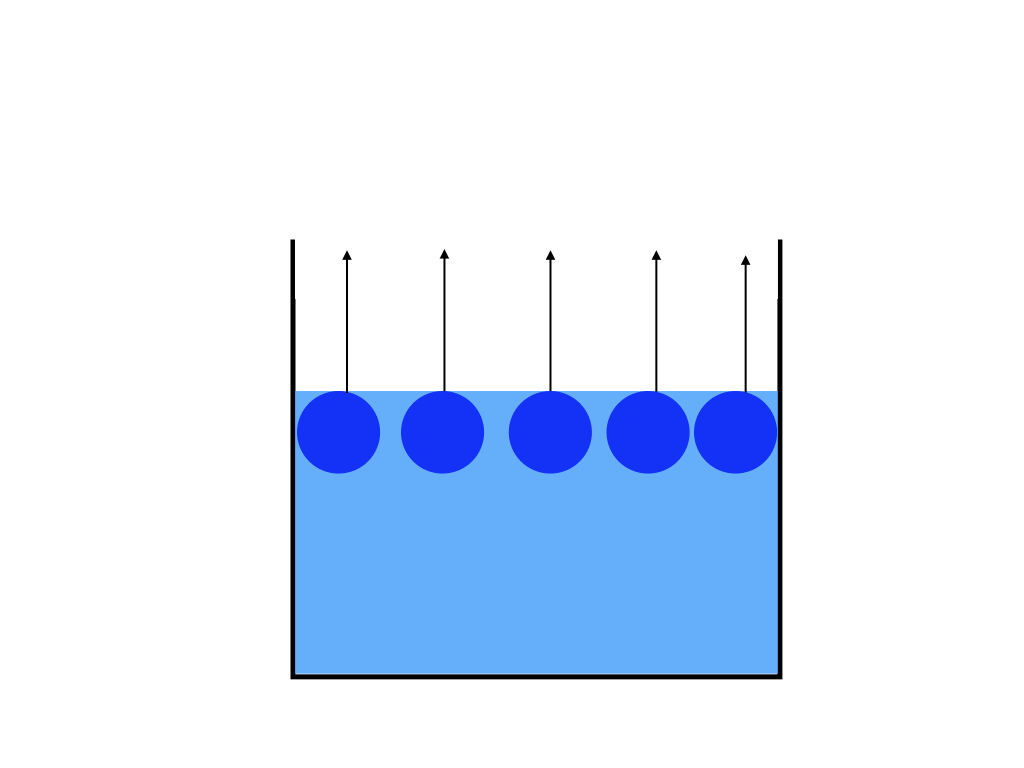
<蒸気圧降下の仕組み図1>
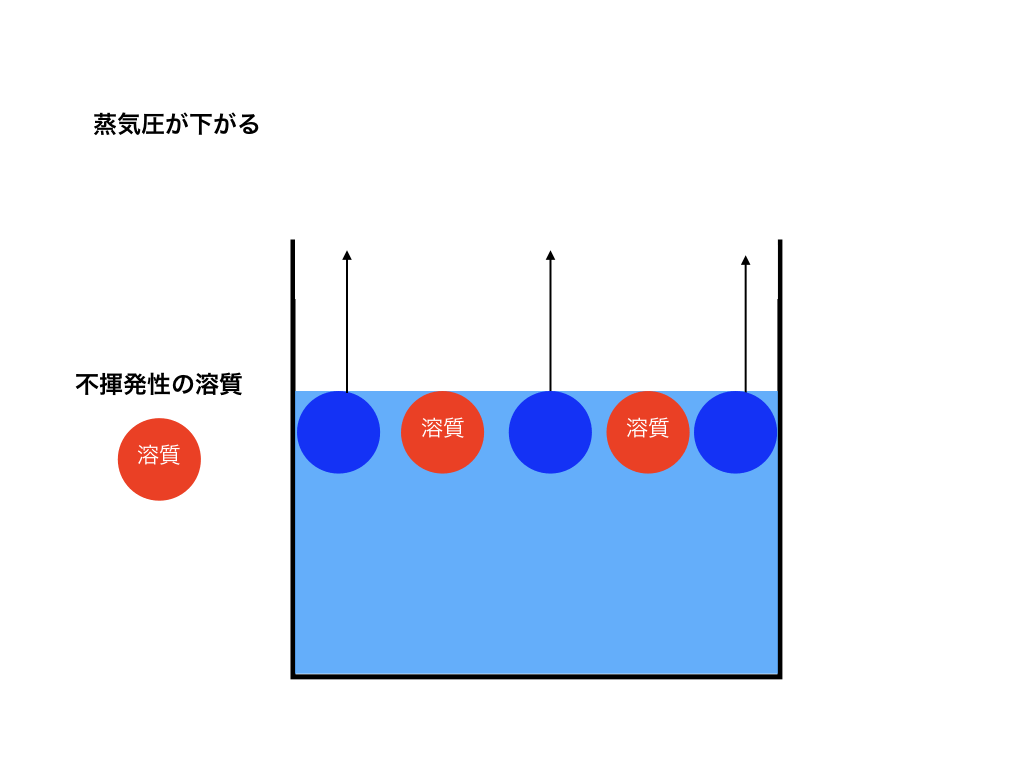
<蒸気圧降下と不揮発性溶質の図2>
つまり、相対的に蒸気圧は低くなります。それが<図3>の様にズレた蒸気圧曲線のグラフです。この現象を「蒸気圧降下」と言います。
沸点上昇の仕組み
蒸気圧降下の仕組みがわかったところで「沸点上昇の仕組み」を学んでいきましょう。
蒸気圧曲線の図
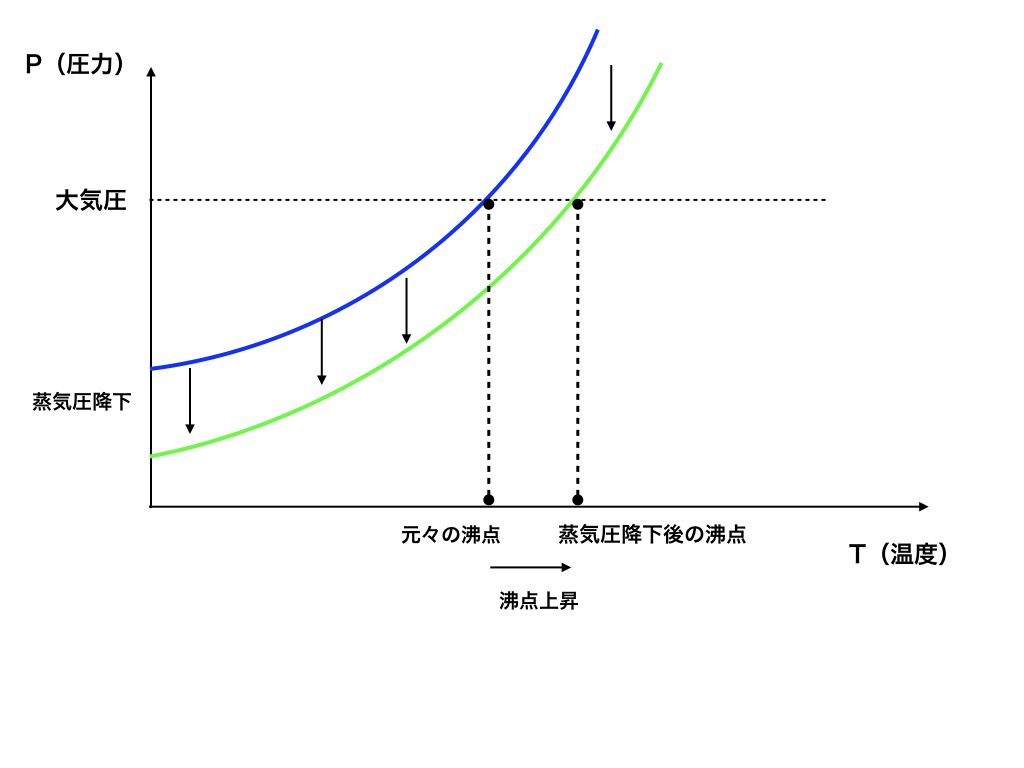
<蒸気圧降下と沸点上昇の説明図3>
蒸気圧降下が起きる事で、同じ大気圧でも沸騰するための温度は高くなる必要が出てきます。<図3>
飽和蒸気圧と大気圧が同じになった時の温度が沸点なのでそれが上昇する=沸点上昇するというわけです。これが沸点上昇の仕組みです。
凝固点降下とは?
凝固点降下も、沸点上昇の時と同様に「凝固点」の意味をしっかりと抑える必要があります。
凝固点とは
凝固点とは、凍っている“(凝固)分子が解け出そうとする数”と、“液体分子が凝固しようとする数”が等しくなった時の温度を意味します。<図4>
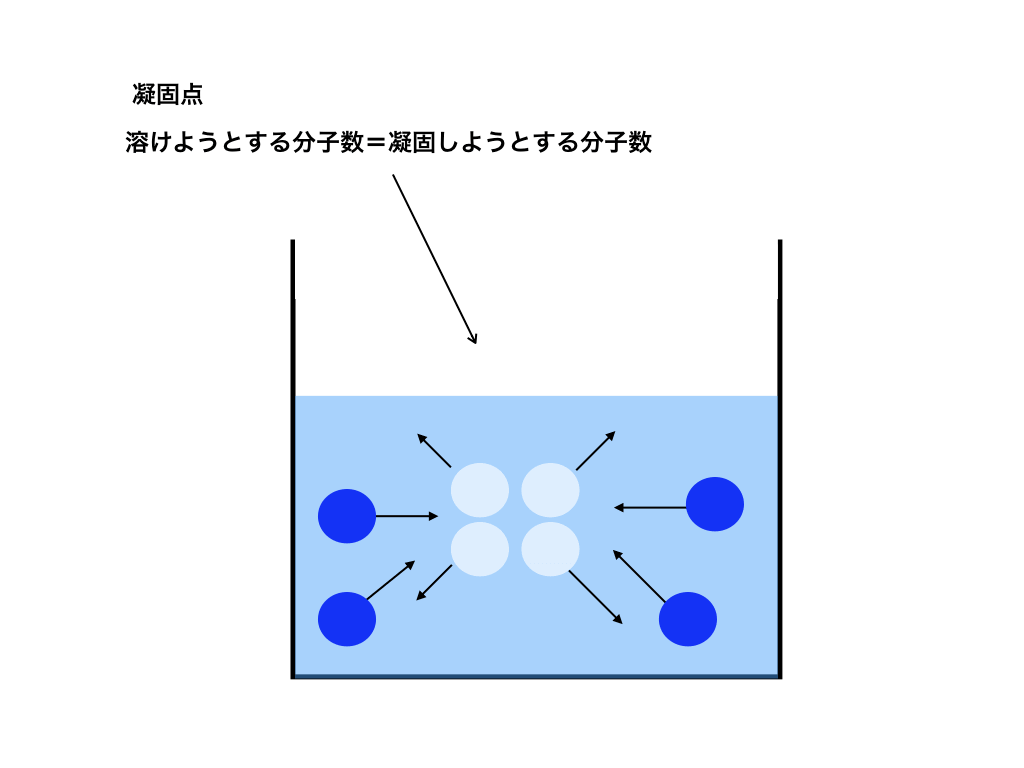
<凝固点の図4>
凝固点降下の仕組み
では、凝固点降下について考えていきます。なぜ、純溶媒に溶質が混ざると凝固点降下を起こすのでしょうか。
実は、溶液が凍り始める時には溶媒分子から凝固していきます!
つまり、溶媒分子のみの場合に対して溶質が混ざった溶液は凝固しようとする溶媒分子数が少ないので、<図5>
さらに温度が下がらないと凝固する分子=融解する分子になりません。その結果として凝固点降下が起こるのです。
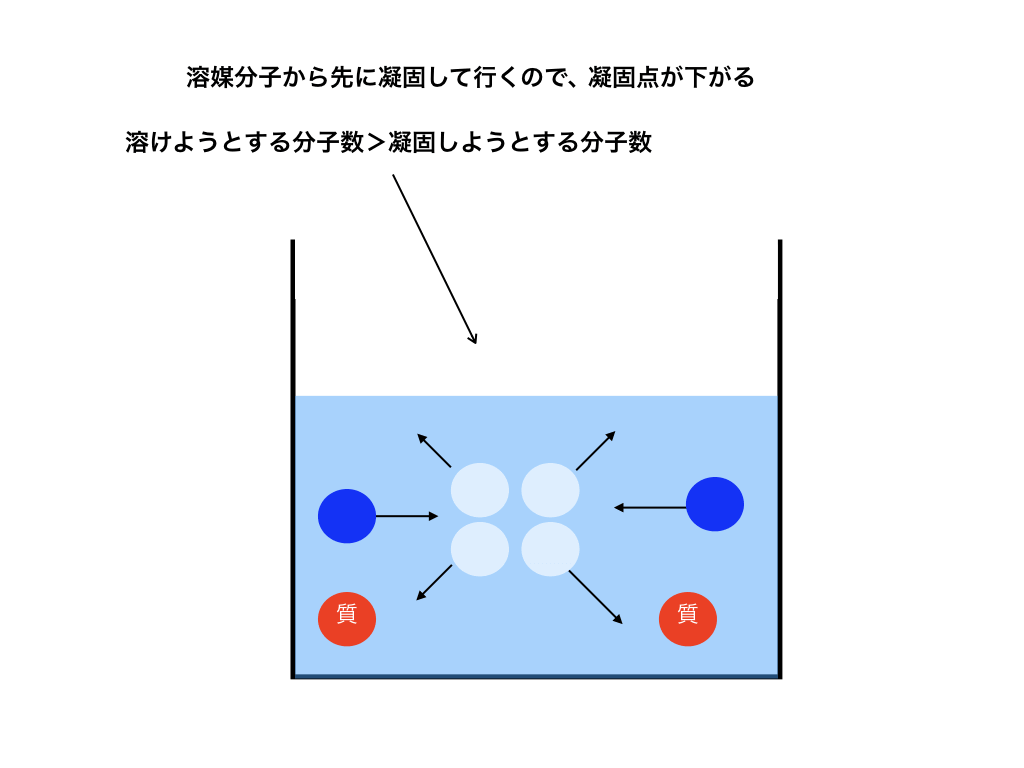
<図5>
この様に、純粋溶媒に溶質分子を混ぜる事で沸騰する温度が本来の温度以上になる事を「沸点上昇」、凝固する温度が本来よりも下がる事を「凝固点降下」と言います。
沸点上昇/凝固点降下の公式:質量モル濃度に要注意!
では、沸点上昇と凝固点降下の仕組みがわかったところで、その公式を見ていきましょう。
理屈がわかれば、沸点上昇と凝固点降下の計算はそれほど難しく有りません。
溶質が非電解質の場合
ここでは、モル濃度(溶質の物質量(mol)/溶液の体積(L))ではなく、
質量モル濃度=溶質の物質量(mol)/溶媒の質量(Kg)を使うことに注意して下さい。
>>「質量mol濃度とmol濃度・質量パーセント濃度の違いと相互変換法を総まとめ!」<<
\(\Delta t=km\)
\(\Delta t\)は温度の変化を意味します。kはモル沸点上昇、モル凝固点降下と言い
、溶媒に固有の定数です。(実際の問題では条件として値が与えられます。)
$$m=\frac {( 溶質のmol数) }{(溶媒の質量kg) }$$
溶質が電解質の場合
この場合特に注意が必要です!
電解質/電離度αとは?
電解質とは、溶媒に溶けてイオン化する(電離する)ものです。
電離度αとは、その電離のし易さを0≦α≦1
(0%:つまり全く電離しない、から、100%電離:全てイオン化する)で表したものです。
例えば、塩化ナトリウムNaClでα=1の時、電離してNaCl→Na +Clともとの2倍のmol数になり、質量モル濃度も同時に2倍になります。
塩化カルシウム\(CaCl_{2}\)ならば、α=1の時、
\(CaCl_{2}→Ca+2Cl \)と元の3倍のmol数、よって、質量モル濃度も3倍。
基本的なレベルの問題では、α=1(すべて電離するものとする)か、α=0(非電解質)しか出題されません。
が、難易度が高くなってくるとαも考慮する問題が出題されるので要注意です。(現在複合問題の解説記事を作成中です)
小まとめ:電解質の計算をする際には、質量モル濃度の変化に注意が必要です。
電離度αについて、酸・塩基反応の範囲でさらに詳しく解説しています。
>>「pH(水素イオン指数)の求め方(電離度が小さい場合)」<<
確認例題3選
では、ここまでで学んだ知識をもとに定着用例題を解いてみましょう。
問題編
沸点上昇の例題
18(g)の\(C_{6}H_{12}O_{6}\)を1.5(Kg)の\(H_{2}O\)に入れた。
この時の沸点上昇度を求めよ。但し、
水\(H_{2}O\)のモル沸点上昇は\(0.52(\frac{Kg\times K}{mol})\)とする。
凝固点降下の例題
4.5(g)のグルコース(\(C_{6}H_{12}O_{6}\))を
1(Kg)の水\(H_{2}O\)に入れた。
この時の凝固点降下度を求めよ。
但し水H_{2}O のモル凝固点降下は \(1.85(\frac{Kg\times K}{mol})\)とする。
溶質が電解質の時の凝固点降下と分子量の計算
9(g)の不揮発性の非電解質Xを1.0Kgの水へとかしたところ 、その凝固点は電離度α=1のKCl、塩化カリウム水溶液:0.1(mol/Kg)の凝固点と同じであった。
この時の電解質Xの分子量を求めよ。
ただし、
水の凝固点降下は\(1.85(\frac{Kg\times K}{mol})\)とする。
解答解説編
少し応用問題があったので、難しい所もあったかと思います。以下に詳しい解答解説を載せているので、
分からなかった部分があればじっくり読んでみて下さい。
沸点上昇の例題の解答
まず、グルコースが(g)で与えられているので、沸点上昇の公式に代入する為にmolに変換します。
グルコース(\(C_{6}H_{12}O_{6}\))の分子量は、
\(6\times 12+1\times 12+16\times 6=180(g/mol)\)
それが18(g)あるので、
$$\frac {18(g) }{180\left( g/mol\right) }=0.1(mol) $$
これを1.5(Kg)の水へ溶かせるので、
$$\frac {0.1\left( mol\right) \times 0.52\left( K\times Kg/mol\right) }{1.5\left(Kg\right) }≒0.0346(K)$$
有効数字二桁で解答して、\(3.5\times 10^{-2}\left( K\right) \)
凝固点降下の例題の解答
こちらの場合も分子量を求めて凝固点降下の計算式に代入するので手順は同じです。
分子量は上で180(g/mol)と求まっているので、同様に
$$\frac {4.5(g)}{180(g/mol)}=0.025(mol) $$
$$\frac {0.025(mol)}{1(Kg) }\times 1.85(K\times Kg/mol)=0.04625(K)$$
\(有効数字二桁で、4.6\times 10^{-2}(K) \)
溶質が電解質の時の解答
これは少し難しいです。凝固点降下度は溶媒に固有の値を持っていて、
溶質(ここでは非電解質Xや塩化カリウムKCl)の種類は関係ありません。
したがって、非電解質Xの分子量を求めるには、
Xの分子量を文字でおいて、(Xの凝固点降下=KClの凝固点降下)の等式を解くことで求めることが出来ます。
\(M_{x}をXの分子量として、\)
水の凝固点降下が\(1.85(Kg\cdot K/mol)なので、\)
$$左辺=\frac {\frac {9\left( g\right) }{M_{X}\times \left( \frac {g}{mol}\right) }}{1\left( Kg\right) }\times 1.85\left( \frac {K\cdot Kg}{mol}\right) $$
右辺(KClの式は、塩化カリウムが電解質で、KCl→K+Cl に電離する事に気をつけながら立式します。)
$$=0.1(mol/Kg) \cdot 2\cdot 1.85(K\cdot Kg/mol) $$
$$右辺=左辺だから、\frac {9}{M_{x}}=0.2\Leftrightarrow M_{x}=45(g/mol) $$
よって、\(Xの分子量は45 (g/mol)。\)
まとめと次回予告(冷却曲線へ)
・沸点上昇と凝固点降下の計算は基本的ですが、前回の<「状態図と飽和蒸気圧曲線」>や次回の<冷却曲線(製作中)>に繋がる非常に重要な分野です。
・また、理論化学だけでなく、有機化学と融合して出題される事もあり(分子量を求めさせて→構造決定をさせる)
大変役に立つので確実に解けるようにしておきましょう。(これは浸透圧でも同じです→「ファントホッフの式と浸透圧がわかる!」)
・次回は、純溶媒とその溶媒に溶質を加えた溶液の温度ー時間グラフ(冷却曲線)を扱います。
今回の内容はそのまま問題になるくらい重要なので「意味/理由」を答えられるように何回も復習しておいて下さい。
溶液シリーズ
<溶液・希薄溶液・気体シリーズ>:「溶液〜気体分野まで高校理論化学を総まとめ!」
第一回:「浸透圧とファントホッフの式をわかりやすく解説」
第二回:「状態図の見方と飽和蒸気圧曲線を読み取る」
第三回:「今ここです」
第四回:「冷却曲線の記述対策と水和物を質量モル濃度へ変換する方法」
今回も最後までご覧いただき有難うございました。
質問・記事について・誤植・その他のお問い合わせはコメント欄、又はお問い合わせページまでお願い致します!
お役に立ちましたら、SNSでシェア&当サイト公式Twitterのフォローをお願いします!

