
状態図と蒸気圧曲線
高校で学ぶ理論化学の中でも、特に気体分野が苦手という人が多いです。
今日はそんなあなたの為に、気体分野でつまずく「きっかけ」の最大の要因である「蒸気圧・蒸気圧曲線」を克服する記事を書いていきます。
その前準備として、はじめに「状態図」を学びます。
これは今後の気体分野だけでなく、その次の壁の「希薄溶液」の「沸点上昇・蒸気圧降下」などにもつながる大切な内容だからです。
では、始めましょう。
(NEW!;続編「蒸気圧降下と沸点上昇/凝固点降下の関係と仕組みが分かる」完成しました。)
目次(タップした所へ飛びます)
状態図とは?
<図一>の様に、ある物質の温度・圧力を変化させた時その物質がどの様な状態の変化(固体・液体・気体と超臨界流体)するかを描いた図の事です。
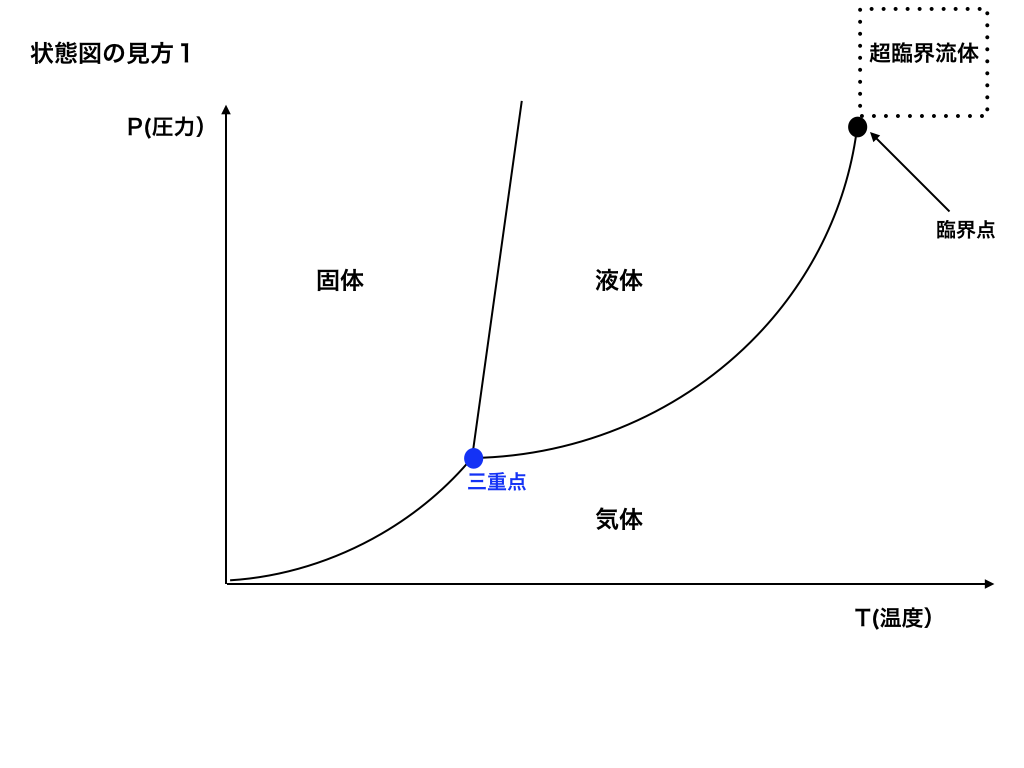
<一般的な状態図>
状態図の見方と特殊な性質を持つ「水」
一つ一つ見方を解説していきます。
一般に、温度が低く圧力も小さい場合には物質は固体で存在します。(図一)の固体部分。
次に、同じ圧力でも温度を上げていくと液体に、さらに気体へと状態を変化させていきます。
最もイメージしやすいのは、「水」だと思います。「氷」→「水」→「水蒸気」と温度を上げると変化していきます。
ただし、後で述べますが「水」に関しては他の物質と少し異なる性質があるので、注意が必要です。
この様な状態変化と、上の気体・液体・個体を区切る線にはそれぞれ名前がついています。
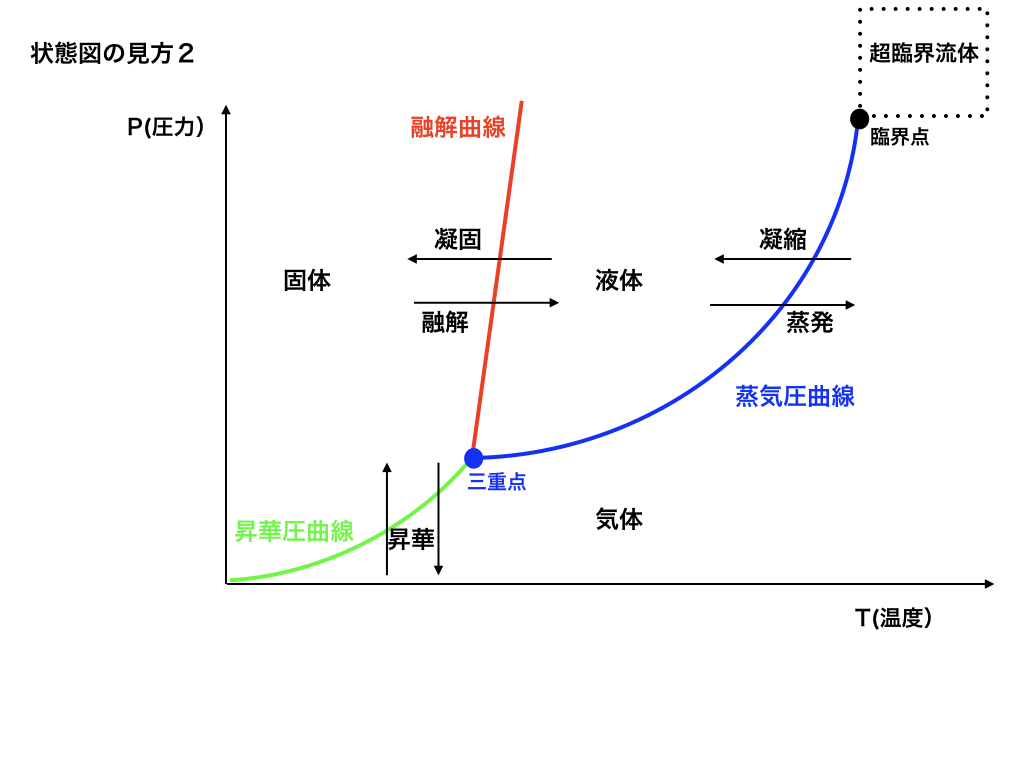
<状態図と気・液・固体>
まず、固体から液体への変化は【融解】、液体から気体へは【蒸発】。
逆に気体から液体へは【凝縮】、液体から個体へは【凝固】
さらに、固体が液体を経由せずに気体になる事があります。それを【昇華】、その逆も反応も同じく【昇華】と言います。
(昇華で有名なものは、ドライアイス(二酸化炭素)です。ケーキなどの保冷剤として入っているドライアイスが白い煙とともに消える(二酸化炭素の気体に昇華している)のは見た事が有るのではないでしょうか?)
次に、固・液・気を隔てている線は、それぞれ【融解曲線】・【蒸気圧曲線】・【昇華圧曲線】と名付けられています。
三重点と超臨界流体
図には、三重点(3つの曲線が交わる点)が有りますがこれは固・液・気の3つの性質を持つ状態になる温度・圧力の事を言います。
また、圧力と温度を共に上げていくと臨界点と呼ばれる点を超して「超臨界流体」と呼ばれる気体と液体の境目がない状態になります。(名前だけは覚えておいて下さい。)
水の状態図でのチェックポイント
先ほど注意が必要と言った水の状態図<図三>をご覧ください。

<水の状態図>
水の状態図の融解曲線が「右下がり」になっています!これは入試でも良く問われるので注意しておきましょう。
飽和蒸気圧曲線と気液平衡
では、飽和蒸気圧曲線の図を見ていきましょう。

<飽和蒸気圧曲線と気液平衡の図>
この図の青色の曲線が蒸気圧曲線です。蒸気圧曲線よりも下の状態であれば、まだ蒸発する余裕がある=全て気体
蒸気圧曲線では以下の項で解説していますが、気液平衡。
飽和蒸気圧曲線よりも上にある状態ならば、「飽和蒸気圧を超えた分だけが凝縮し液体」となります。
これは、飽和蒸気圧を超えた圧力では液体から気体へと飛び出しても、その容器はすでに気体分子で一杯(飽和状態)なので直ぐに液体に押し戻されるイメージです。
蒸気圧曲線上では何が起こっているのか

<蒸気圧曲線上で起きている気液平衡>
蒸気圧曲線上では、図のように液体から蒸発する分子数と、液体に戻ろうとする気体分子数が釣り合った状態にあります。これを【気液平衡】と言います。
この曲線よりも下に有れば、全ての液体の分子が蒸発して気体のみになります。
確認例題:全て気体と仮定せよ!
では、この記事の理解度チェックと、有名なテクニックの紹介の為の例題をみて下さい。
状態方程式を使用するので、先に確認しておきたい人は→「理想気体の状態方程式をマスター」をご覧ください。
$$問題:フタをしてある容積33.6L、57℃の箱に、$$
$$0.5molのエタノールを入れる。$$
$$エタノールの蒸気圧が57℃で4.0 \times 10^{4}Paの時の圧力を求めよ。$$
$$ただし、R(気体定数)を8.31\times 10^{3}(Pa・L/K・mol)とする。$$
解説:この様に、箱の中が気体のみなのか、気液平衡・気液共存なのかが分からない時は
【とりあえず全て気体になっているものと仮定して計算する】という鉄則があります。
仮定が正しければ計算が成立し、仮定が間違いだったときは飽和蒸気圧よりも計算上の圧力が大きくなり計算があわなくなります。
<解答>したがって、箱の中のエタノールが全て気体であると仮定すると、理想気体の状態方程式より、
$$P'\times 33.6=0.5\times 8.31\times 10^{3}\times (273+57)$$
$$P'=\frac {5\times 831\times 330}{33.6}$$
$$\Leftrightarrow P'≒ 40800≒ 4.1\times 10^{4}$$
状態方程式より、もしエタノールが全て気体になっていれば
$$その圧力は4.1\times 10^{4}ですが$$
57℃=330K(ケルビン)での飽和蒸気圧は$$4.0 \times 10^{4}Pa$$であったので、計算した圧力が飽和蒸気圧を
$$(0.1 \times 10^{4}Pa)$$
上回ってしまいました。これは、「エタノールが全て気体になっている」という仮定に反する為、一部は液体である事がわかります。
そして、この様に一部が液体のまま
(存在している時の気体の圧力)=(飽和蒸気圧)なので、
$$答えは4.0 \times 10^{4} (Pa)となります。$$
・整理すると、まず全て気体と仮定して状態方程式を解き、その圧力(P'とする)と飽和蒸気圧Pの関係が
(一)P'=Pの時、気体の圧力はP’=飽和蒸気圧P。
(二)P'>Pの時、気体の圧力は飽和蒸気圧Pで一部が液体。
(三)P'<Pの時、気体の圧力は、状態方程式で計算した圧力P'で全て気体。
となります。
次回予告:希薄溶液の沸点上昇・凝固点降下へ
今回の内容、特に飽和蒸気圧は理解し辛い範囲なので良く復習しておきましょう。
そして、問題集等に載っている類題を解いて見てください。
次回は、今回学んだ蒸気圧をもとに「沸点、凝固点の意味」と「希薄溶液の沸点上昇・凝固点降下」を解説していきます。
→完成しました。「蒸気圧降下と沸点上昇/凝固点降下の関係と仕組みが分かる」を続けて読む。
溶液シリーズ
第一回:「浸透圧の求め方とファントホッフの式がわかる!」
第二回:「(今ここです)状態図の見方と蒸気圧曲線の読み取り方」
第三回:「蒸気圧降下と沸点上昇/凝固点降下の関係と仕組みが分かる」
第四回:「冷却曲線と水和物の扱い方が得意になる」
今回も最後までご覧いただき有難うございました。お役に立ちましたら、シェア&当サイト公式Twitterのフォローをお願いします!
質問・記事について・誤植・その他のお問い合わせはコメント欄又はTwitterまでお願い致します。

