円とその周辺(図形と方程式:1)
<この記事の内容>:図形と方程式でも頻出の『円』の式と接線、具体的な問題などよく出るポイントだけをまとめました。
<関連する記事>:「数学B:ベクトル方程式で円を表す」「数学Ⅲ:複素数平面での円とアポロニウスの円」
※:2019/06/28更新:図形と方程式(円)第三回まで完成しました。
目次(タップした所へ飛びます)
円の方程式と様々な表し方
ここでは、具体的な図形(円)をx-y座標平面に置き方程式を使って図形問題を解いていく方法を紹介していきます。
円の方程式(中心が原点/原点でない場合)
まずは最も基本的な原点を中心とし半径がr(rは0以上)である円と、その方程式を見て見ましょう。
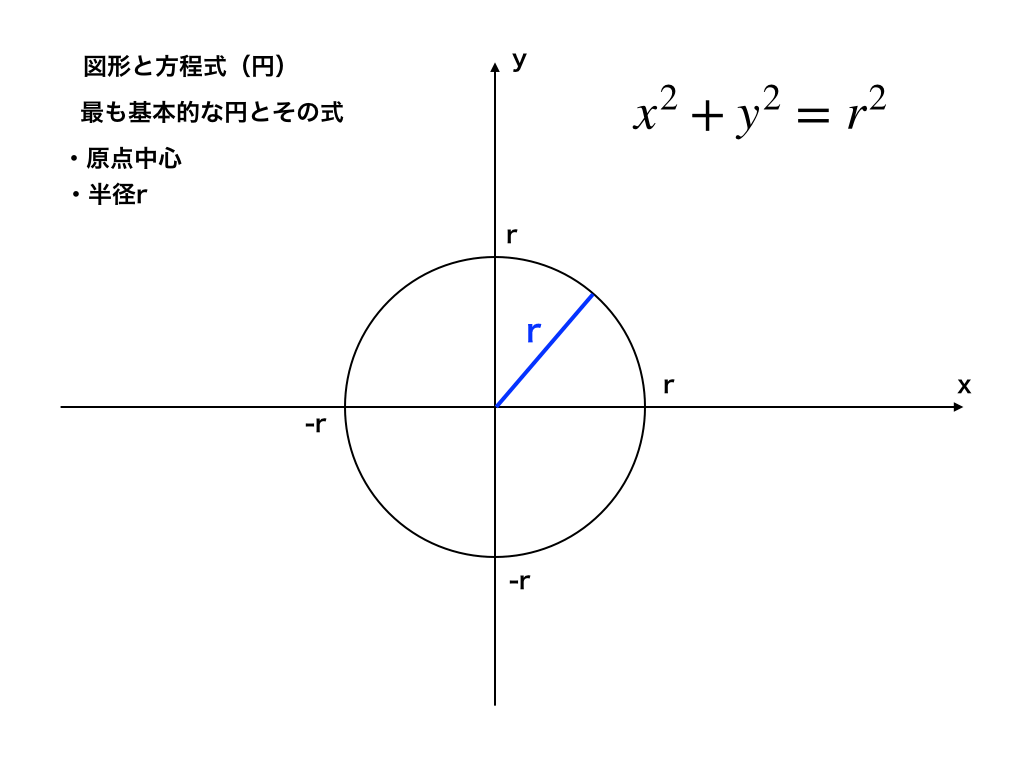
<原点=点C>
原点以外が中心の時
次に中心が【原点以外】の場合です。上で示した方程式をx軸正方向に\(\alpha\),y軸正方向に\(\beta\)平行移動させると考えて、その式は$$(x-\alpha)^{2}+(y-\beta)^{2}=r^{2}$$と表せます。
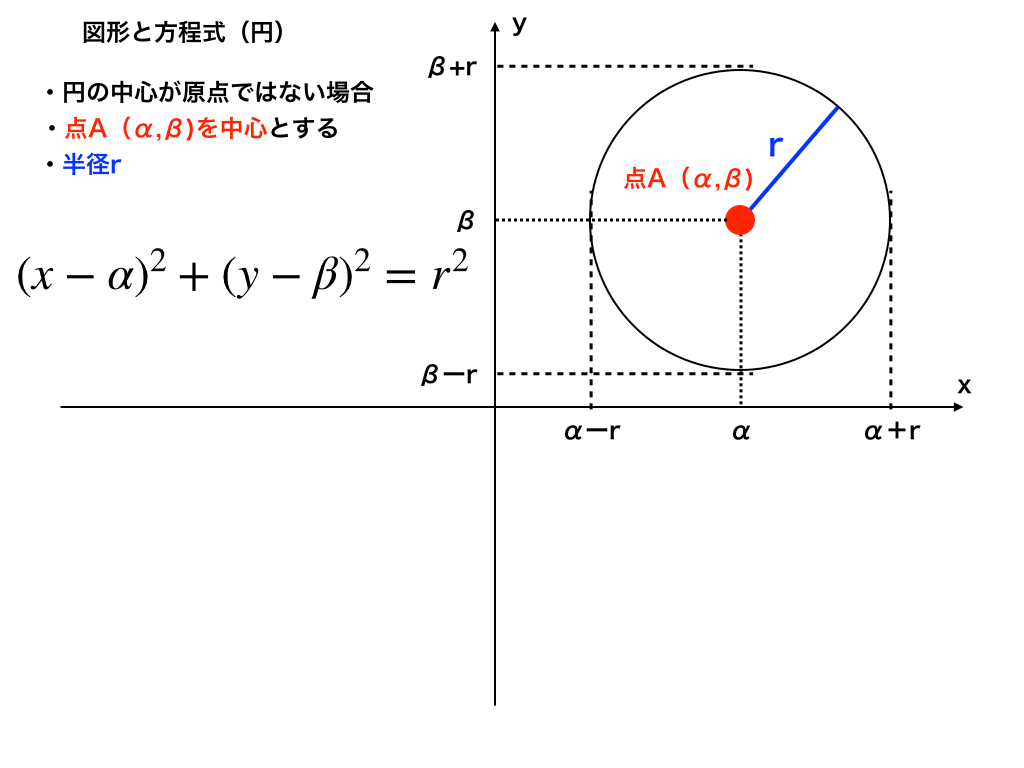
<円の平行移動>
円の方程式(一般形)
直線の方程式にも『y=ax +b』(のy軸との切片と傾きで表す形)と『ax+by+d=0』(一般形)が有るように、円についても一般形での式が存在します。
それは、\(ax^{2}+bx+cy^{2}+dy+e=0\)で、これを平方完成の要領で変形していくと、先ほどの\((x-\alpha)^{2}+(y-\beta)^{2}=r^{2}\)の式に帰着します。
ベクトルや複素数平面での円の式
なお、円を表す式は図形と方程式の分野以外でも、『ベクトル』や『複素数平面』で頻出です。ここで一旦チェックしておきましょう。
ベクトル方程式での円
詳しくは「ベクトル方程式を一から学ぶ」で紹介していますが、次のように円は2種類のベクトル方程式で表すことが可能です。
1つは中心点と円周上の点の距離(絶対値)が一定(r=半径)であることを利用し、
もう一つは<図2>のように、直径の両端と円周上の点Pを結んだ時に“円周角の定理”から角度が90度→内積が0である、ということから導くことが可能です。
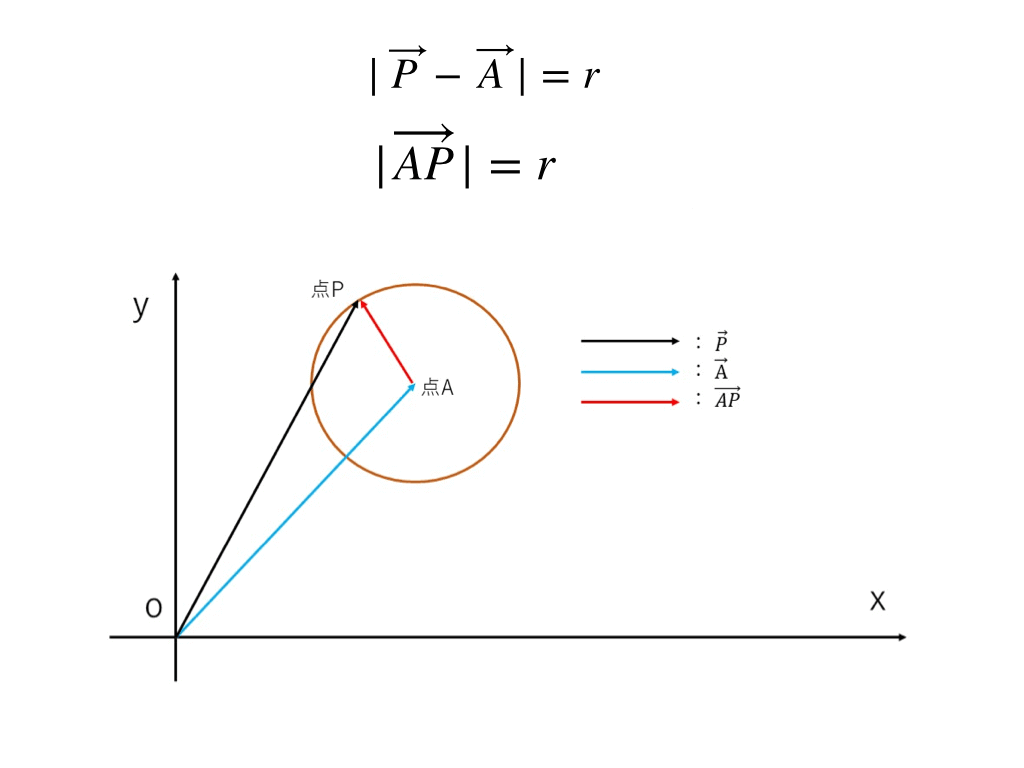
<ベクトル方程式(円1)>
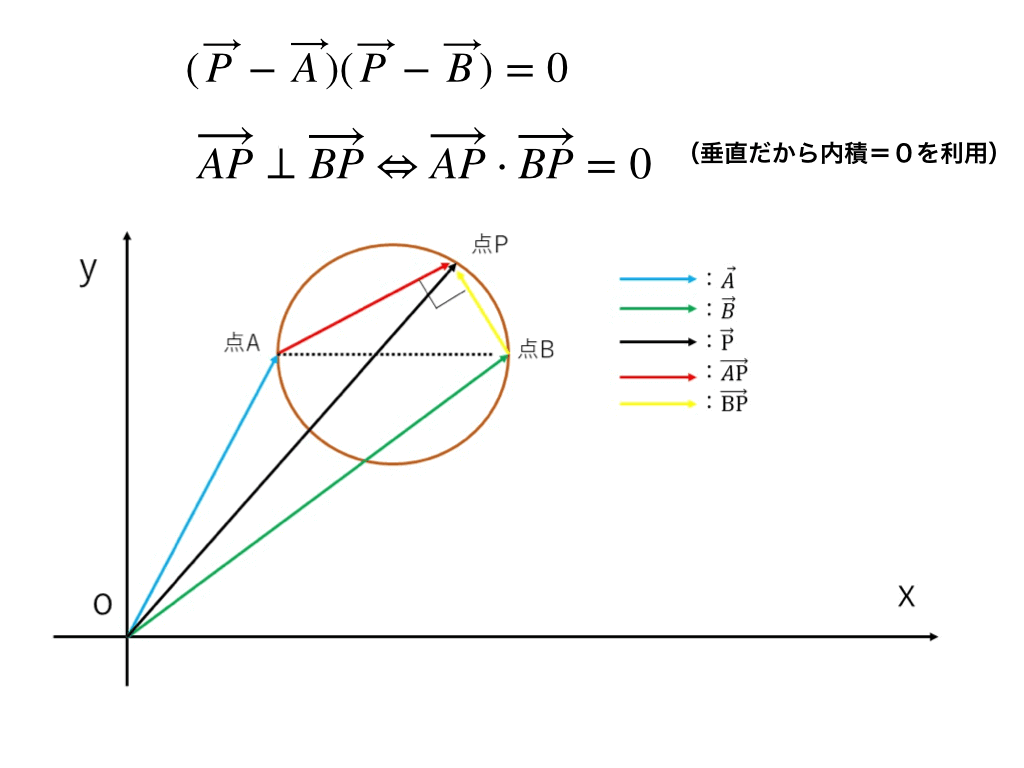
<ベクトル方程式(円2)>

複素数平面での円の式
複素数平面【数学Ⅲ】でも同様に、\(|z-\gamma|=r\)の形で円を表せます。
以下の例\(|z-2|=3\)のように中心(2,0)からの距離が一定(上のベクトル-1と同じ考え方)であること使った方法です。
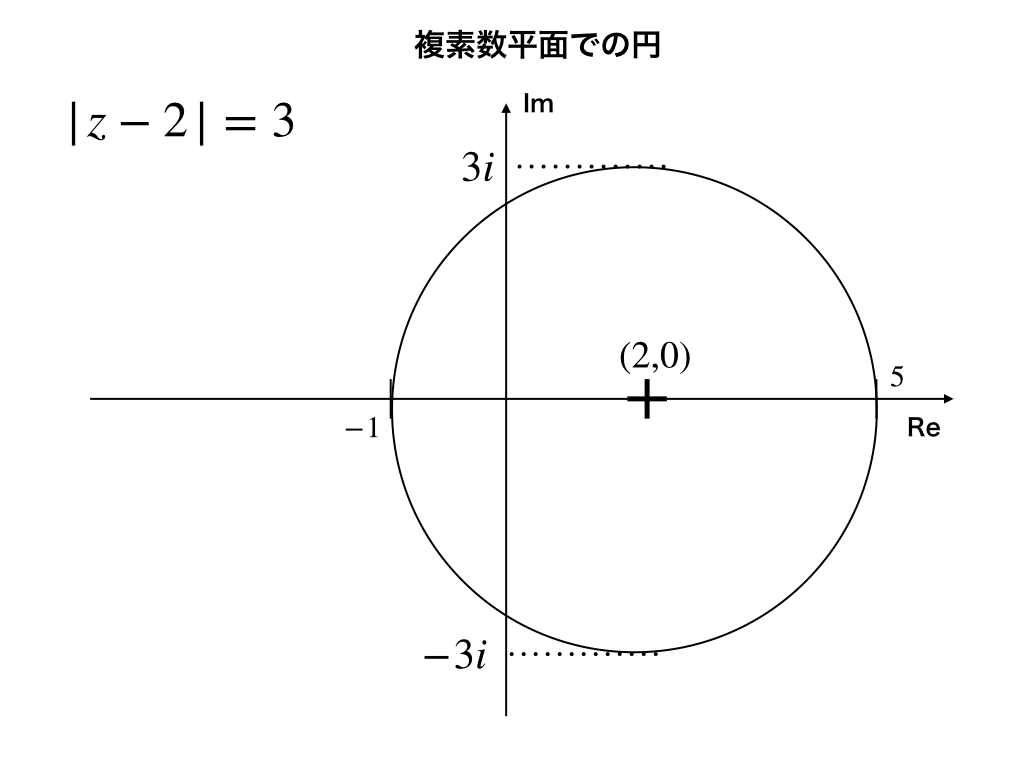
<ガウス平面での円>
円(図形と方程式)の問題(上)
ここからは、具体的にどのような問題が出題されるかについて、【特に重要なもの】を中心に紹介していきます。
(今回は以下の2題、次回は円の接線(下)+《2つの円の関係や共通接線》に関する応用問題を扱います)
直接が切り取る弦の長さの求め方
1問目:座標平面上に円があるとき、それを直線が貫いているような、交点が2つある場合を考えます。
その交点と交点を結んだ『弦』の長さ(イメージ図のオレンジ色の部分)を求める問題です。
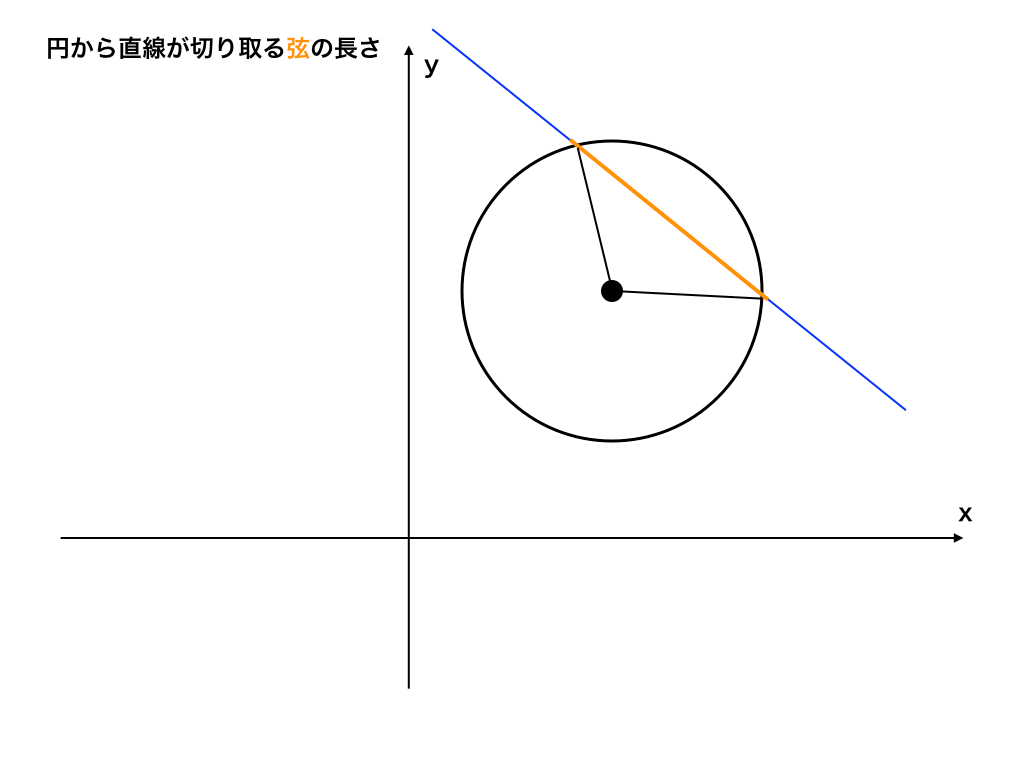
(イメージ図)
(応用問題1):いま、\(直線l:-x+y+2=0\)が、\(中心点(2,2),半径r=\sqrt{6}\)の円から切り取る弦の長さを求めよ。
解答解説1
このタイプの問題は、『点と直線の距離』の公式と三平方の定理を用いて解いていきます。
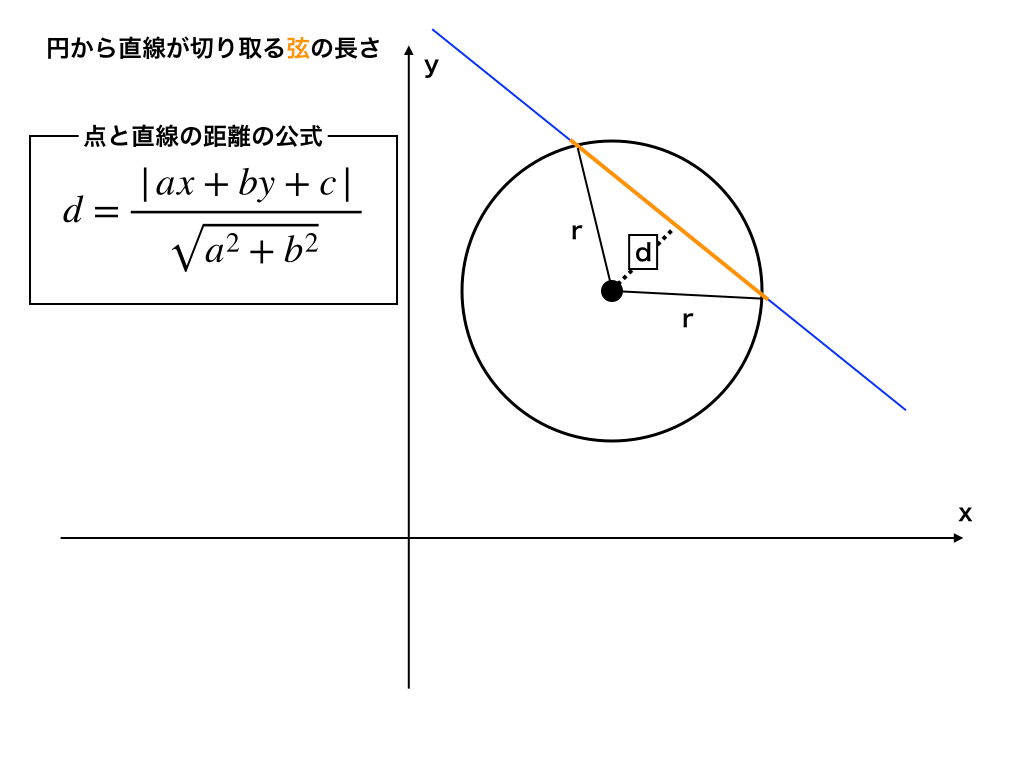
上のイラストのように、【弦の長さの半分=mとすると】mは、円の中心から直線に下ろした垂線dと、半径r、そしてmで出来た直角三角形について三平方の定理を使うことで求める事が出来ます。
従って、dは点と直接の距離公式$$d=\frac{|ax+by+c|}{\sqrt{a^{2}+b^{2}}}$$より、\(d=\sqrt{2}\)、\(r=\sqrt{6}\)
よって、m=2
\(この2倍が弦の長さなので、2・2=4・・・(答)\)
外側から円に向かって引いた接線
第2問:円の外側の点から引いた2本の接線の式を求める問題です。(イメージ図2)
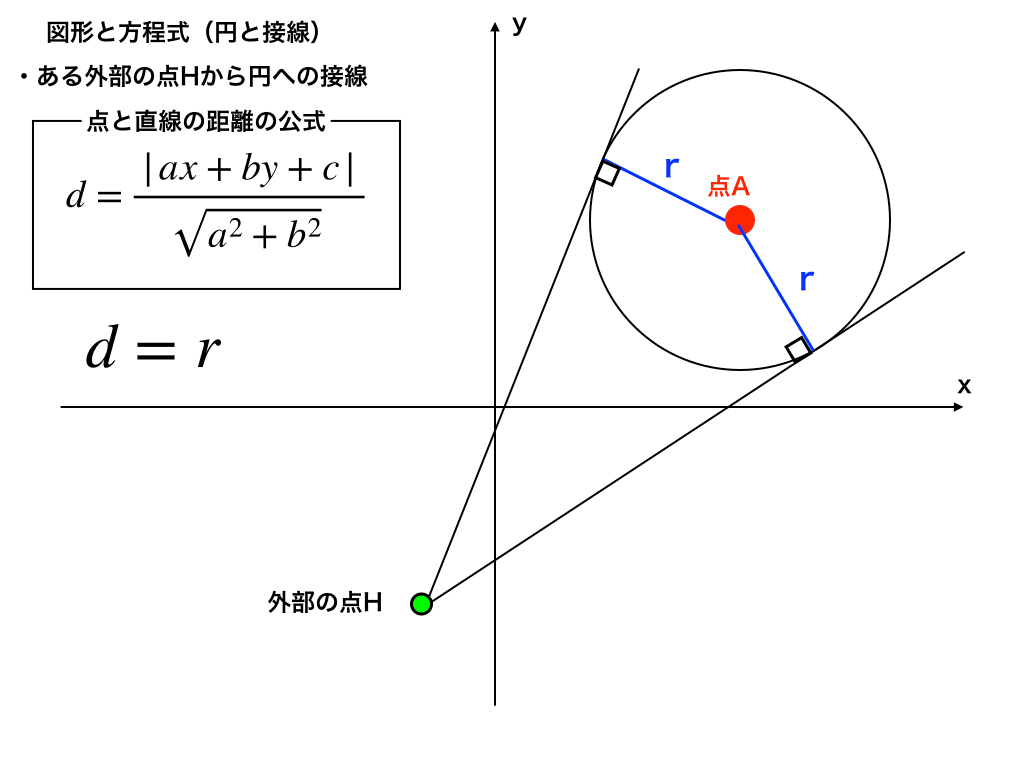
(イメージ図2)
次回以降で紹介する、『接線に関する応用問題』のキソとなる超重要問題なので、必ず解き方の流れを理解しておきましょう。
応用例題2:いま、\(中心点が(5,5),半径rが2\)の円に向けて円の外側の\(点H(-1,-3)から接線を2本引いた。\)この時の接線の傾きを求めよ。
問題は『接線の傾き』ですが、はじめにおく式に求めた値(傾き)を代入することで接線の式(2つ)も計算することができます。
解答解説2
まず接線の方程式が分からないので、傾きを未知数kとして立式します。
この接線は点Hを通ることから、\(y-(-3)=k(x-(-1))\)展開して\(0=kx-y+k-3\)。
つぎに、円の中心と接点の距離dが半径r=2と等しいことを利用して
$$d=\frac{|6k-8|}{\sqrt{k^{2}+1}}=2$$
$$この式を解くとk=\frac{6\pm \sqrt{6}}{4}$$
よって傾きは\(\frac{6\pm \sqrt{6}}{4}\)・・・(答)
今回のまとめと次回へ
・今回は円の方程式2通りと、ベクトル・複素数平面での円の式を紹介しました。
・また、円の接線の式を求める方法と、直線が切り取る『弦』の長さを計算する方法について解説しました。
・次回は円の応用問題(下)として、さらに応用的な問題の解法を解説していきます。
図形と方程式シリーズと関連分野の記事一覧
図形と方程式(一):「今ココです」
図形と方程式第二回:「円の応用問題(2つの円の関係や共通接線etc,,,)」
図形と方程式第三回:「円の交点を通る直線や曲線(束)を解説」
・ベクトル分野は「ベクトルとは?0から学ぶ記事まとめ」
・複素数平面は、「複素数平面の解法解説まとめページ」より、それぞれご覧ください。

