内分点・外分点とその応用
<この記事の内容>:数2「図形と方程式」の基本となる内部/外分の座標の求め方と、特に苦手な人が多い【外分点の場所】の探し方について紹介しています。
さらに、その応用と確認として、数学Ⅲ【複素数平面】上での”図形の外分点”に関しても解説しました。
<関連記事>:「複素平面第1回:極形式と直交座標」
※2019/06/07更新:「複素数平面の解説記事まとめ」を作成しました。
目次(タップした所へ飛びます)
外分点と内分点(図形と方程式)
まずは、図形と方程式の範囲で学ぶ内分点/外分点の座標を求める公式から見ていきます。
内分点の座標公式
外分点の前に、内分点の公式と位置について復習していきます。(これは、本題の外分点の位置を考える時に内分点の位置を考える方法を利用するためです)
簡単な内容ですが、いま一度しっかりと確認しておきましょう。
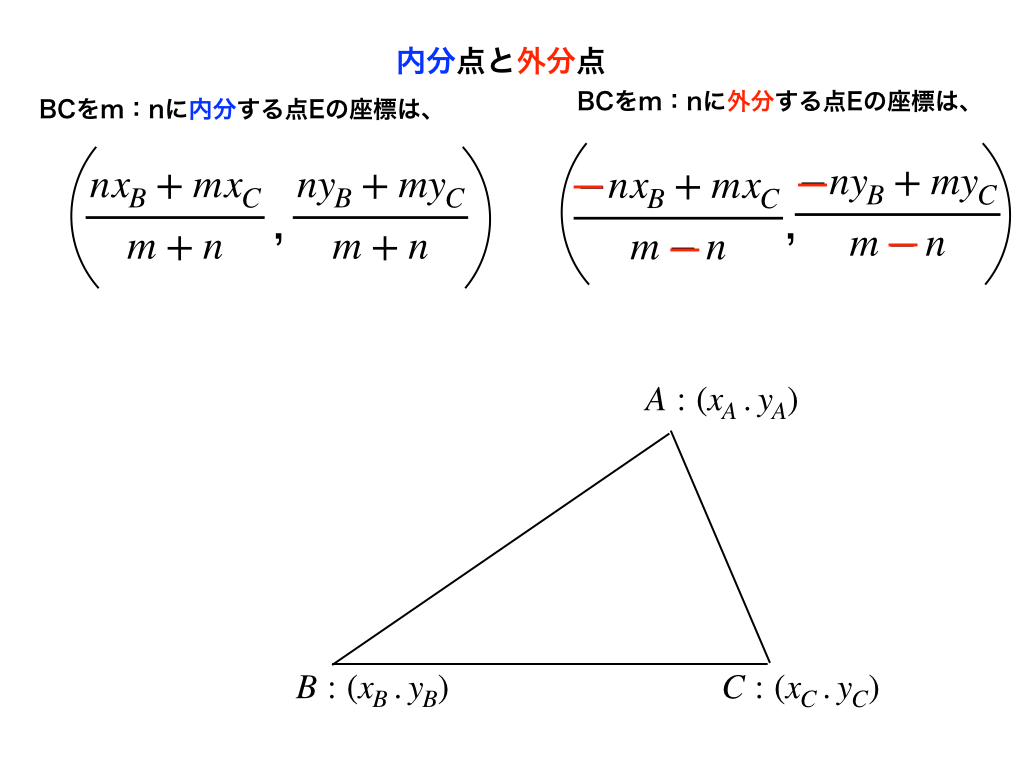
<内分・外分点の座標公式>
例題1:具体例で習得
実際に問題を解いていきながら効率よく習得しましょう。
(問題1):三角形ABCの各頂点の座標がそれぞれA(4,8),B(2,3),C(7,4)であるとき、辺BCを2:3に内分する点の座標を求め、その点を図示せよ。
解説1:内分点
まず、点Eの座標について:先の公式通り計算することによって\(4,\frac{17}{5}\)と計算できます。
また、”内分”する点Eの位置はBCを5等分してBからCへ2つ進んだところが答えとなります。
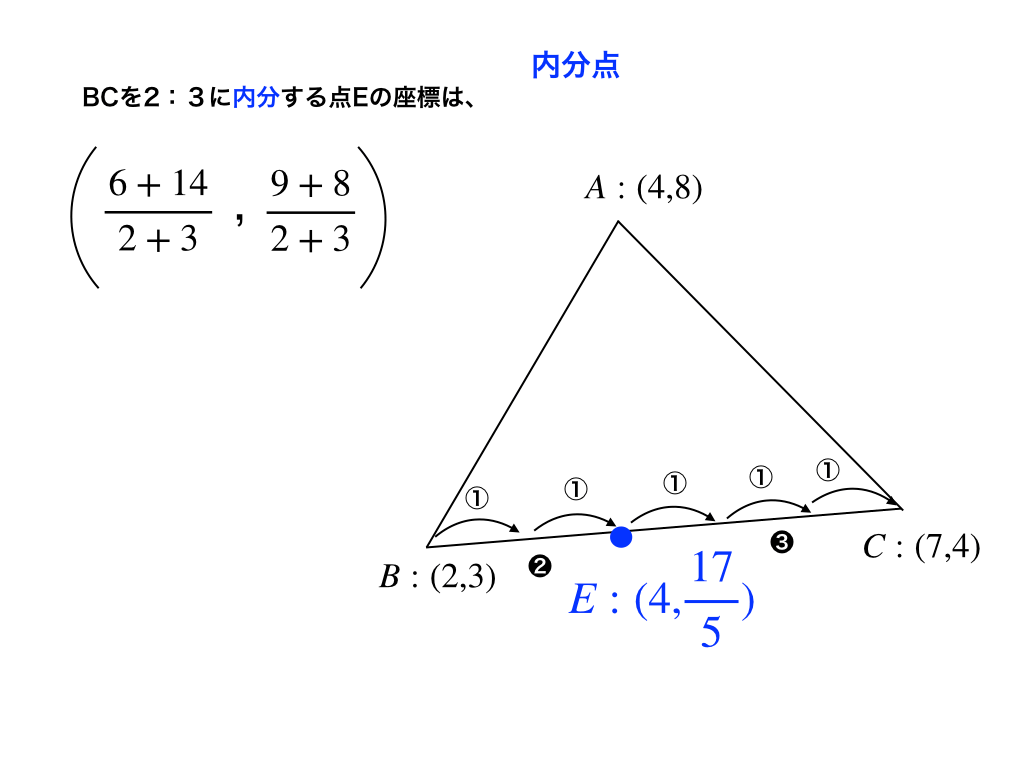
<例題1の解説>
外分点
では今回の本題である、“外分点“に入っていきます。多くの人は先ほどの公式を使って座標を求める事には慣れているのです。
が、座標を与えられずに“点◯と点△をm:nに外分する点を図示する”ような問題になると、途端に解けなくなってしまうのです。
外分の具体例と位置を求めるコツ
このような時は、先述したように内分点の考え方を少し手を加えて応用することがコツになります。
(例題2):先ほどと同じ三角形ABCのBCを2:3に【外分】する点Eの座標と、その位置を図示せよ。
解説2:m:nに外分→m:-nに内分と考える(イラスト参照)
外分点の座標は公式で求めることができ、今回は点E\(-8,1\)です。
一方で外分の位置を図示する際には、見出しに書いたように「“片方をマイナスにし、\(2:-3\)に内分”する」という考え方を用います。
ここではBから2つ分だけ進んで、逆向き(マイナス)に3つ分進んだとき、点Cに到達する点が外分点Eとなります。
2:3に外分する→2<3より点Eは線分BCのB側に存在し以下の図の場所にあることが分かります。
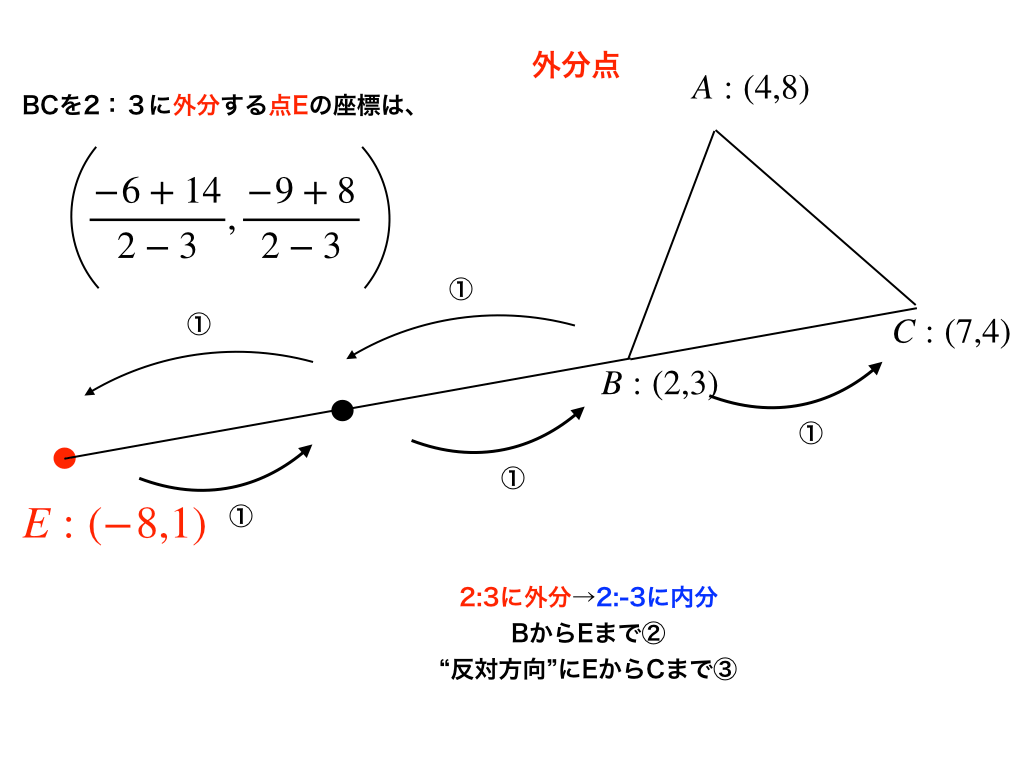
<例題2の解説>
重心の求め方
+αとして、重心の座標を求める公式にも触れておきます。
これはいたってシンプルで、\(\frac{三角形の3つの頂点の座標の和}{3}\)で計算する事が可能です。
重心の座標を計算する
ここでは、計算の過程のみを載せておきます。
$$G_{x}=\frac{4+2+7}{3}=\frac{13}{3}$$
$$G_{y}=\frac{8+3+4}{3}=5$$
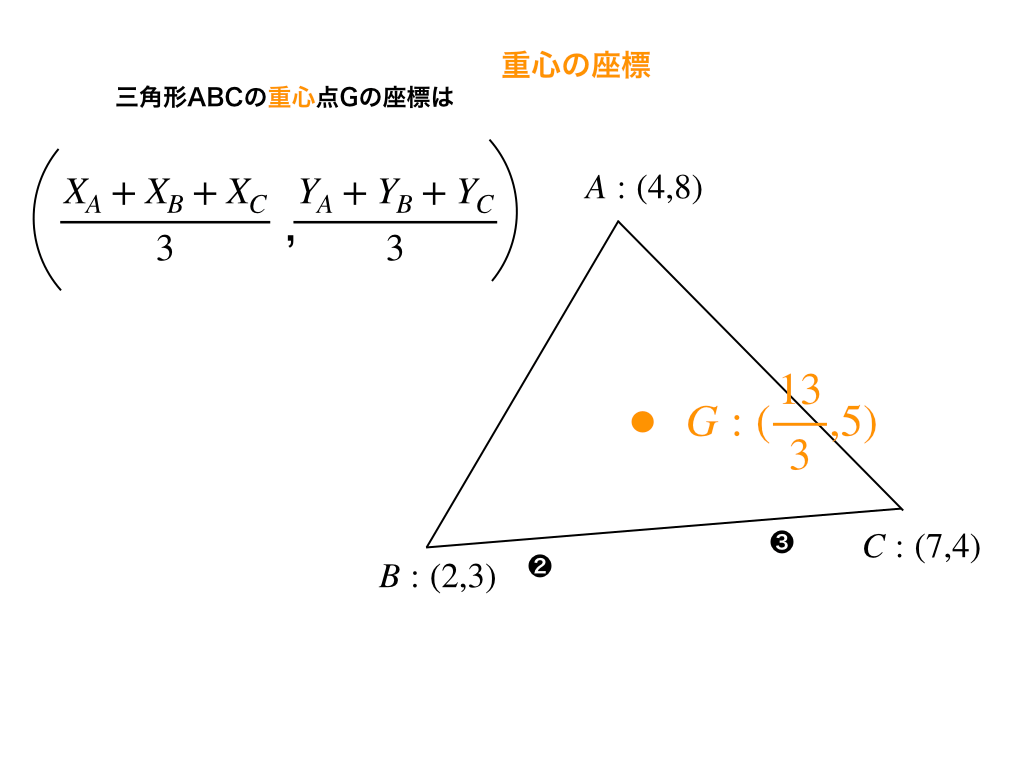
<例題3:重心の解説>
内分・外分点の応用(複素数平面)
ここから先は数学Ⅲの複素数平面での内分・外分点について扱うので、文系の方は(作業自体はほとんど変わらないので)復習がてらに、理系の方は必ずマスターする様にしましょう。
演習:やる事は同じ!
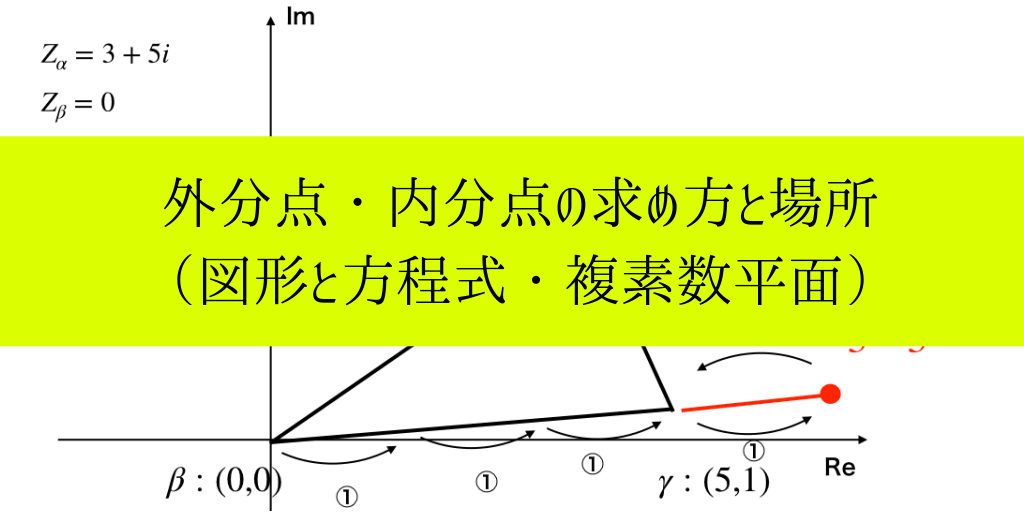
(演習問題):複素平面上に、\(Z_{\alpha}=3+5i,Z_{\beta}=0,Z_{\gamma}=5+i\)を各頂点とする三角形αβγがある。
このとき辺βγを4:1に外分する点δの直交座標を求め、その位置を図示せよ。
演習の解答と解説
解説:まず問題で与えられた条件をもとに三角形αβγを複素平面に描きます。
そして、
・辺βγを【4:1】に外分する事=辺βγを4:-1に内分することと、
・4>1(先ほどと不等号の向きが逆です!)であることより、
辺βγの点βから4つ進み、1つ戻る(-1)と点γになる、以下の図上の赤の丸で示した部分が「点δ」であることが分かります。
また点δの座標は、公式より
$$\frac{0\times -1 +4\times 5}{3}=\frac{20}{3}$$
同様に
$$\frac{0\times -1 +4\times 1}{3}=\frac{4}{3}$$
より、点δの座標は\(\frac{20}{3},\frac{4}{3}\)と求めることができました。
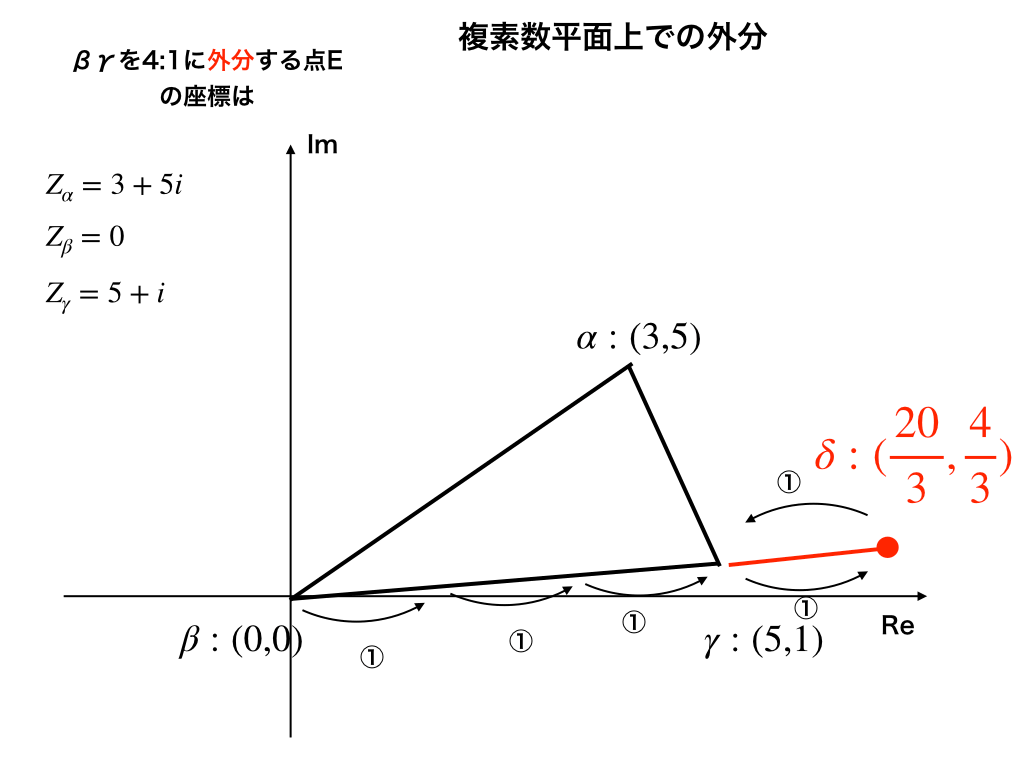
<演習:複素平面編>
内分点/外分点のまとめと続編
・内分/外分点 +重心の座標公式は必ず使えるようにした上で、
・外分点を求める際に「比のどちらの数字が大きいか」(→点が飛び出す方向が分かる)
+
・m:nに外分→m:ーnに内分を意識して、適切な位置をすぐに浮かぶようになるまで類題等で復習するようにしておきましょう!
・次回は、複素平面(五)として複素数特有の式変形や図形との関連を解説していきます。
複素数平面&図形と方程式の関連記事
〜複素数平面シリーズ〜
総まとめ:「複素平面を0から応用まで解説!記事まとめページ」
複素数平面第1回:「複素平面のキソと極形式⇔直交形式」
複素数平面第2回:「極形式の掛け算と割り算の図形的な意味と証明」
複素数平面第3回:「今ここです」
複素数平面第4回:「ド・モアブルの定理とその応用」
(NEW!)複素数平面第5回:「アポロニウスの円と複素平面での軌跡」
今回も最後までご覧いただき、有難うございました。
「スマナビング!」では、読者の皆さんのご意見/ご感想や、記事のリクエストの募集を行なっています。ぜひコメント欄にお寄せください。
また、snsでB!やシェアをしていただけると大変励みになります。
・ご依頼などの上記以外のご連絡に付きましては、お問い合わせページよりお願い致します。

