電磁力とローレンツ力 +フレミングの法則
<この記事の内容>:電流が磁界から受ける”電磁力”と、混同しやすい”ローレンツ力”との関係、力の向きを調べる”フレミング左手の法則”の使い方などをイラストを用いて解説しています。
<これまでの記事>:「高校物理・物理基礎:電磁気分野のまとめ」,ローレンツ力(問題編1)作成しました。「ローレンツ力による荷電粒子の運動1」
目次(タップした所へ飛びます)
電磁力の向きと強さ
電流が流れているところに磁場がかかると『電磁力』という力が働きます。
ここでは、その方向を調べる”フレミング左手の法則”と電磁力の大きさの公式を紹介していきます。
フレミングの左手の法則
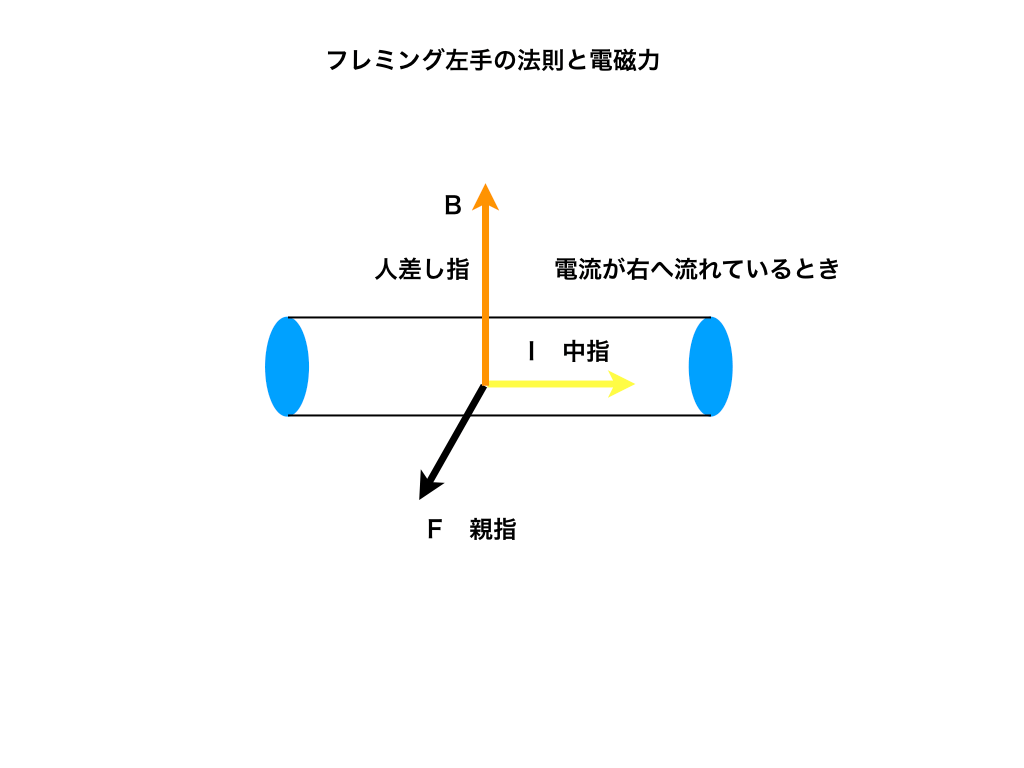
フレミング左手の法則は、以下の<図1>のように
・『電流Iが流れている方向』と
・『磁場Bの向き』が分かっていれば、左手を以下のように使うことで
・『電磁力Fの向き』が分かるという法則です。
同様に、”電磁力の向きを調べる方法”には右手を利用するものもあるのですが、まずは基本であるフレミング左手の法則をマスターしましょう。
(次の項で別の方法を解説した記事を紹介しています)
<図1:電流と磁場の向き>
向きを調べる手順
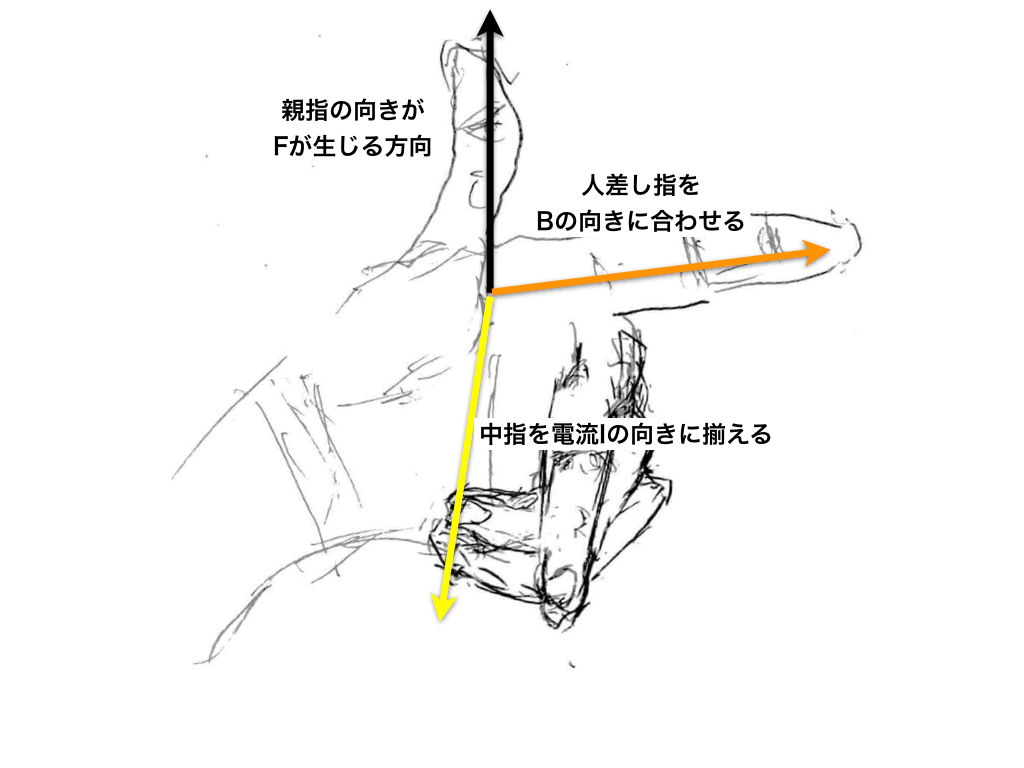
はじめに人差し指を磁場の向き、中指を電流の向きにそれぞれ揃えた上で、その両方に直交する方向の親指の先の方向が”電磁力がかかる向き”です。
<図2:左手の法則>
※フレミング左手の法則で問題が解きづらい、という方へ:”右手の法則”と呼ばれる別の方法で電流・磁場の向きから電磁力の向きを求めることができます。
詳しくは>>「磁場を切って進む導体棒(電磁誘導2)の最後の項」を参照してください!
電磁力の大きさの公式
電流が磁界から受ける電磁力F(N:ニュートン)は、磁束密度B(T:テスラ)・電流I(A:アンペア)、そしてその力がかかる”長さ”をℓ(m)としたとき、\(F=B\times I\timesℓ\)で計算できます。
問題に頻出の◉や⊗の記号と矢印
さて、向きと強さの公式がわかれば、いわゆる”電線を並べた問題”など色々な問題を解くことが出来ます。
その際、問題の図に”○の真ん中に・を入れた記号”や、”○に×を入れた記号”が書かれているかと思います。
これは”電流の向き”と”磁場の向き”、”力の向き”の3方向を紙面で表す際、3次元の空間では考えづらいので、わかりやすくするために使用されるものです。
ただし、問題を解き始めた頃はどちらが裏から手前に向かっていて、どちらが表から裏向きなのか分からなくなりがちなので、矢印のイメージとともに以下の図で紹介しておきます。
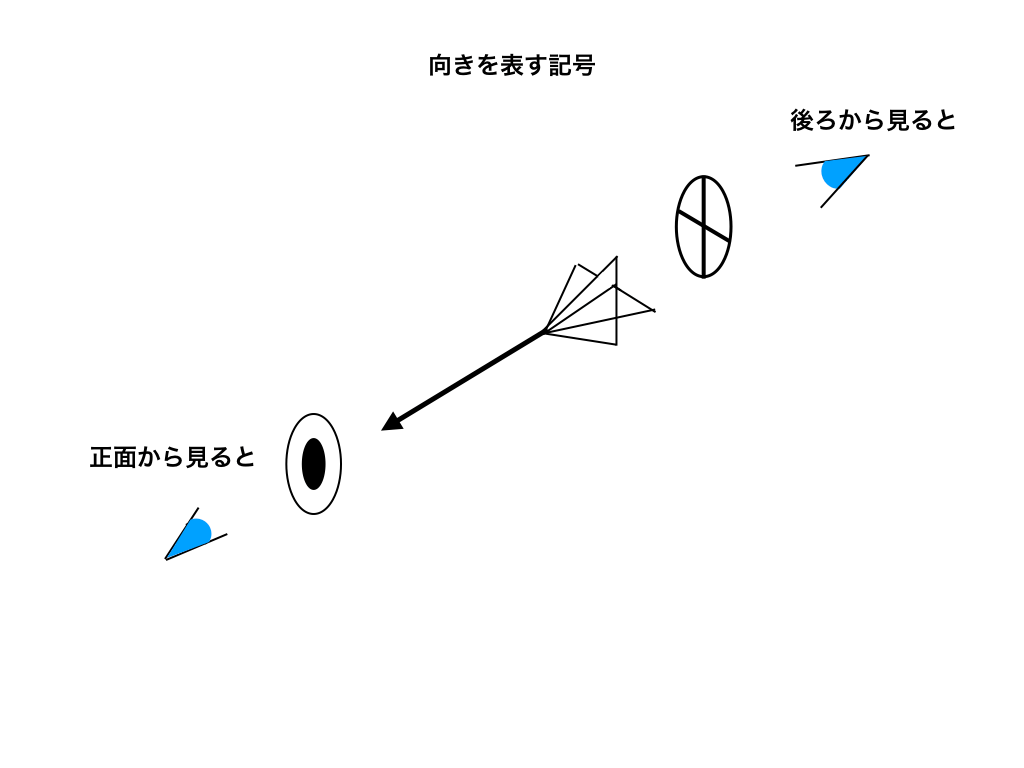
<矢印の先の記号と矢じりの記号>
ローレンツ力とは?電磁力との関係
次は電磁力とローレンツ力の関係についてみていきます。
電磁力との違い(関係)とローレンツ力の大きさ
さて、電磁力とローレンツ力の関係は(特に初学者には)非常に理解しづらいものの一つです。
ここでは、電磁力とローレンツ力の大きさの公式を見ながら、この2つの関係を解き明かしていきます。
電荷の電気量をq(C:クーロン)、速さをv(m/s)として、
電磁力:F=BIℓ
ローレンツ力:F=Bqv
と表されます。
ここで、共通しているのはBのみで全く違うように見えます。
しかし、「電流とは?I=envSの公式の意味と導き方」で紹介したように(まだご覧になっていない方はぜひ参考にしてください)電流Iは電荷(電子)が移動することで起こるものなので、実は非常に深いつながりがあるのです。
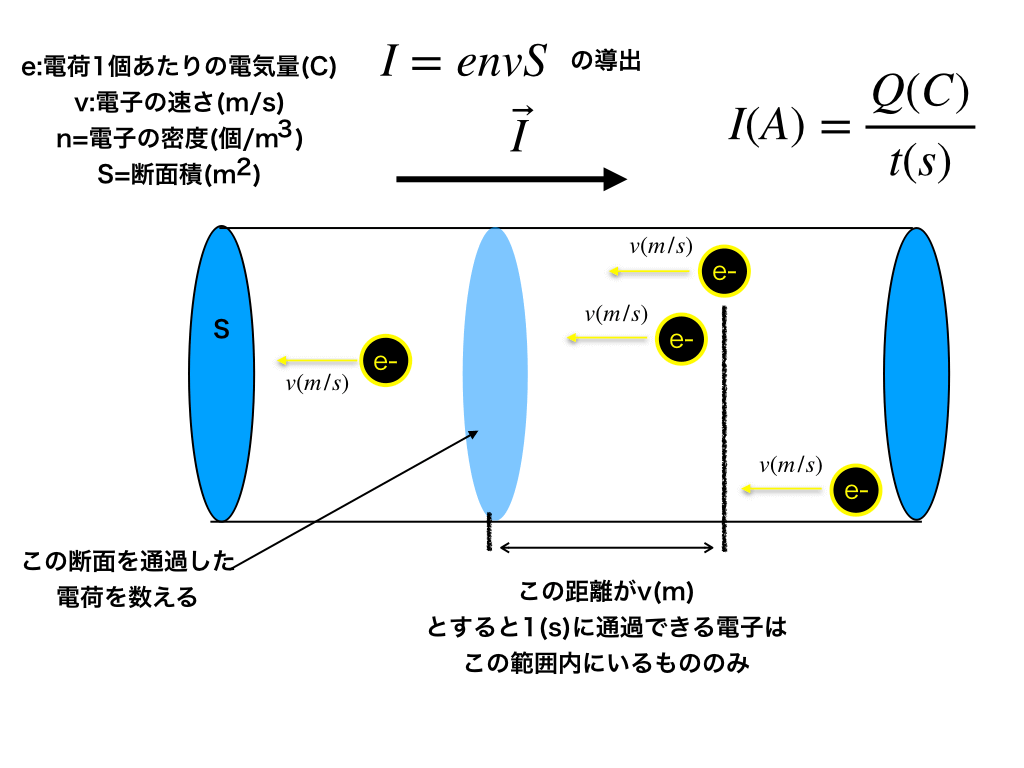
<電流と電子の関係図>
ローレンツ力の総和=電磁力
いま、e(C)の電荷が長さℓ(m)・断面積S\((m^{2})\)の導線中に、\(n(個/m^{3})\)の密度で存在するとします。
電荷がv(m/s)で移動しているとき、ローレンツ力は"f=Bev"で表されて、電磁力はF=BℓIと書く事が出来ます。
ここで、ℓ(m)の導線中にある電荷はSℓn(個)なので、"f=Bev"に"Sℓn(個)"をかける事によってローレンツ力の総和が求まります。
\(f・(ℓ中の電荷の個数)=BevSℓn\)さらに、先ほど紹介したI=envSより、
\(=Bℓ・envS。従ってF=BℓI\)
となってローレンツ力の式から電磁力を導くことができました。
ローレンツ力の向きとフレミングの法則再び
さて、上の項では”電荷によるローレンツ力の集まりが電磁力と一致する”ことを解説しました。
このことを考えると、ローレンツ力の向き(qが正・負の両方の場合で)もフレミング左手の法則で調べることが出来ます。
すなわち、以下の図のように
・負電荷が移動するときは、電流が流れる方向と逆向きに中指を向け、
・正電荷が移動するときは、電流の向きと一致するのでフレミング左手の法則がそのまま使えるのです。
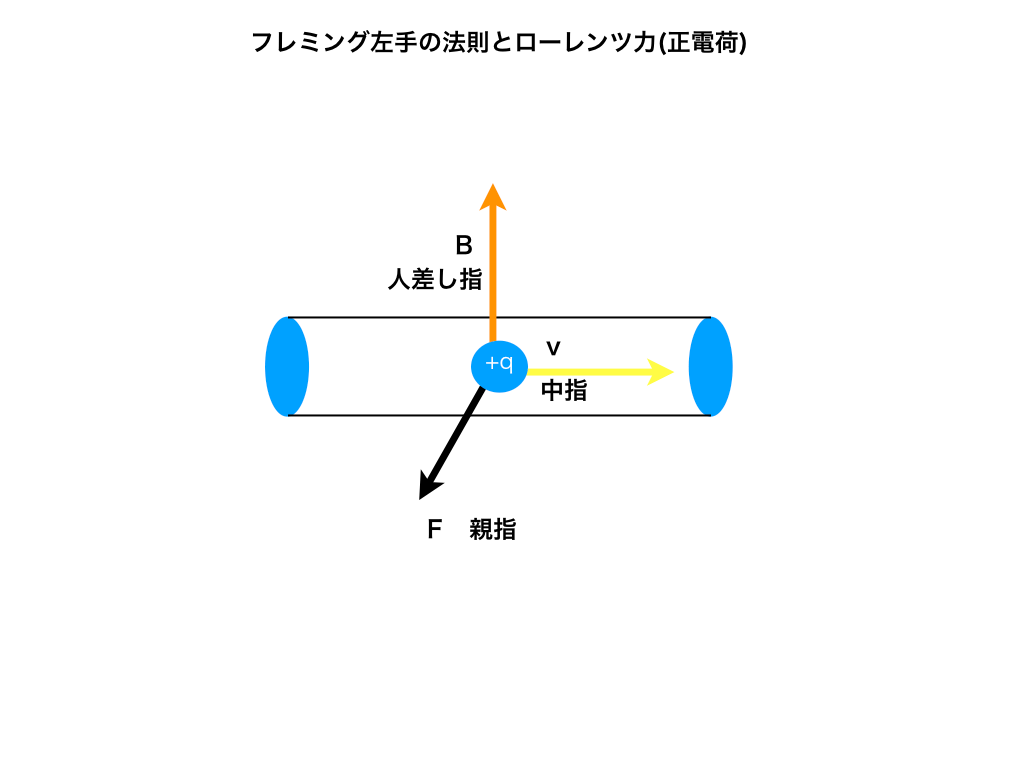
<正電荷によるローレンツ力とフレミング左手の法則>
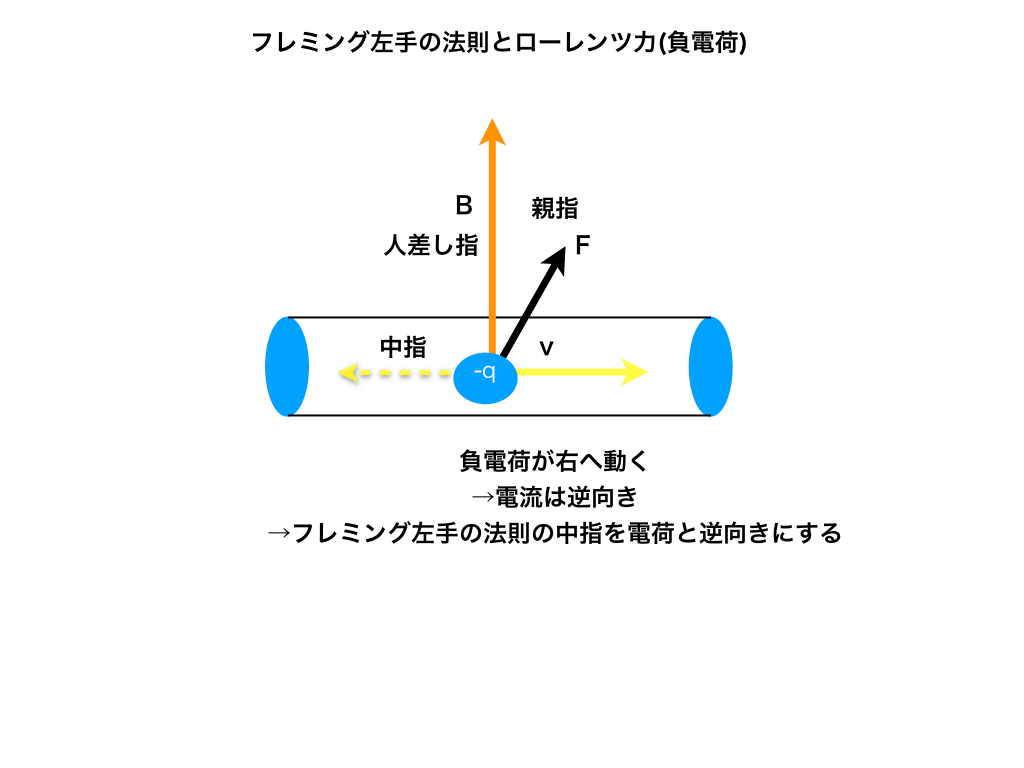
<負電荷によるローレンツ力>
まとめと続編「電磁・ローレンツ力の問題編」へ
・電磁力やローレンツ力の”向き”を調べるフレミング左手の法則と、それぞれの力の大きさを計算する公式をしっかりと頭に入れておきましょう。
・≪ローレンツ力ひとつひとつが集まったものが”電磁力”になる≫という2つの力の関係は非常に大切なです。
・次回は、電磁力やローレンツ力を実際に使用する問題を紹介しながら解法の解説を行います。
電磁気の関連記事一覧と次回へ
電磁気分野の記事一覧は「高校物理の”電磁気”総まとめページ」でご覧いただけます。
(磁気分野)
第1回:「電流が作り出す磁場の大きさとその方向:右手(右ねじ)の法則を徹底解説」
第2回:「今ここです」
第3回:「電磁力・ローレンツ力を例題を使って身につける!(問題編1)」
第4回:「応用編:サイクロトロンの原理と例題」

