
二次曲線(円錐曲線)第1回:円錐曲線と呼ばれる理由と『放物線』
<このシリーズの中身>:数学3『二次曲線』で扱う曲線のグラフや方程式、それぞれの特徴などをまとめました。
<今回の内容>:それぞれの二次曲線(放物線・楕円・円・双曲線)と円錐の関係を前半で解説し、後半ではその内の『放物線』の方程式の導出と、グラフなどをみていきます。
目次(タップした所へ飛びます)
二次曲線とは?種類と円錐との関係
上述した通り、高校数学で扱う二次曲線は『楕円』(+円)・『双曲線』・『放物線』があります。これらは全て次の項で紹介する「円錐の断面」である、という共通点があります。
円錐の切り口が二次曲線になる
以下の図のように、円錐を切る角度によって二次曲線(と底面と平行に切った場合は『円』)ができます。これが、楕円、双曲線、放物線と(円)が『円錐曲線』と呼ばれる所以です。
円と楕円
実際に、円と楕円が断面にあらわれる切り方を見てみましょう。
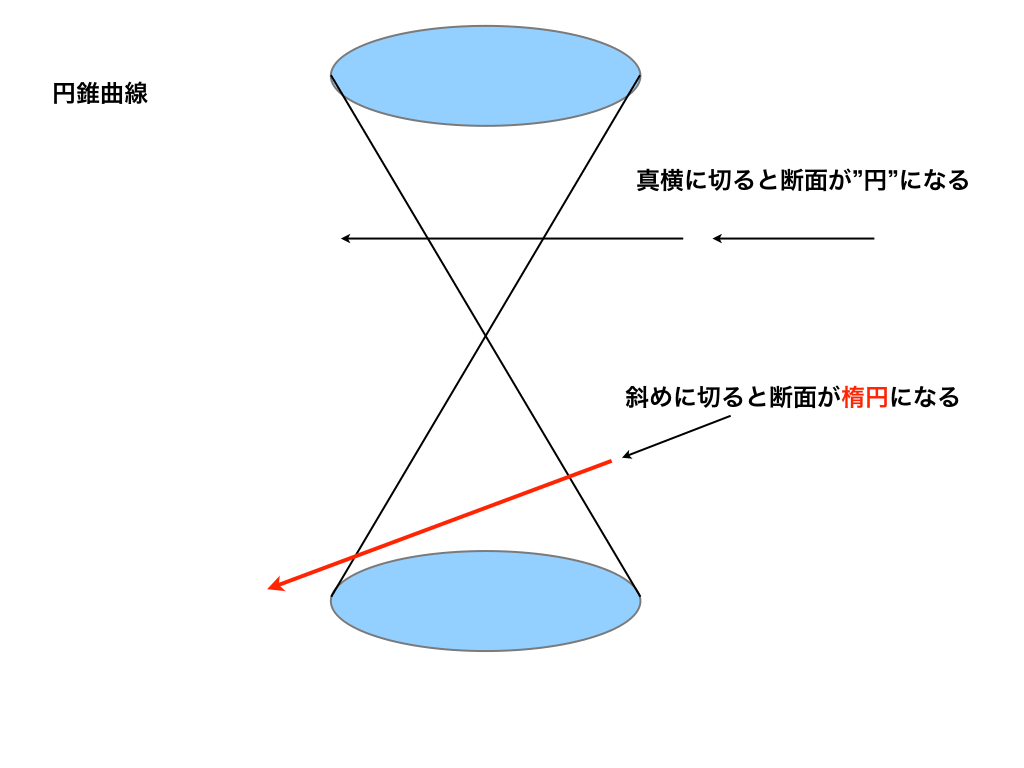
上の図のように、円錐の底面に平行に切ると「円」、斜めに切ると「楕円」となります。
放物線と双曲線
今度は、放物線と双曲線が断面になる切り方です。円・楕円・放物線と違って、双曲線は上下につなげた2つの円錐を切った断面であることに注意しましょう。
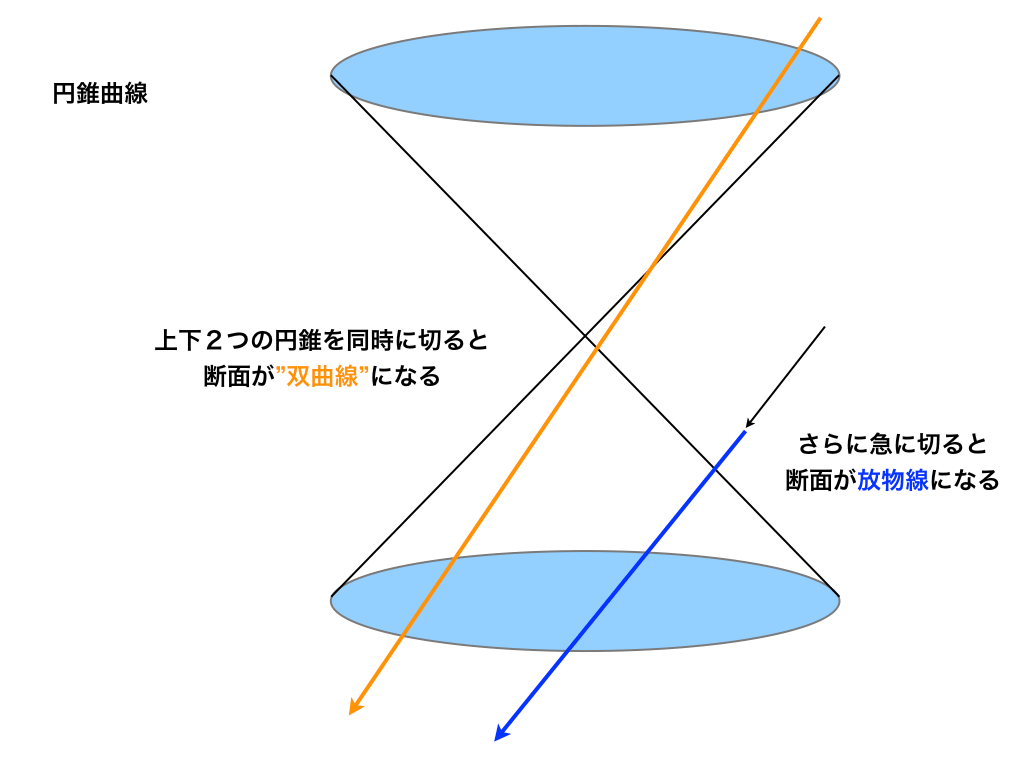
これも解説した通り、楕円の切り方の角度を急にすると『放物線』であり、円錐2つを切り取った断面が『双曲線』になることがわかります。
二次曲線と軌跡(それぞれのルールを満たす点の集合)
これから、実際に二次曲線を見ていきます。いずれも(例:『焦点Fから曲線上の点Pの距離と、準線からPまでの距離が同じ点の集合』)といった決まりがあり、それを満たす軌跡になっていることを覚えておきましょう。
放物線とは
ここからは実際に二次曲線の式を導き、特徴・用語などを紹介していきます。3種類(円を含めると4種類)ある二次曲線のはじめとして、最もなじみのある"放物線"から解説します。
y=x2はその代表的なものですが、数学3の「式と曲線」で扱う放物線は以下のような定義に従います。
放物線の定義
さてこれまで何気なく扱ってきた放物線ですが、『焦点F』からの距離と、『準線』からの距離が等しい点(=これが点Pです)の集合と定義されます。(準線に関しては以下の図を参照してください)
放物線の式の導出
ここからは、点Pの軌跡を求めることで放物線の式を導出してみましょう。
まず点Pの座標を(x,y)、焦点Fを(0,a)、さらに準線の式をy=-aとします。
さらに、点Pより準線に下ろした垂線の足をQとすると、上述した放物線の定義より『PF=PQ』が成り立ちます。
PF=PQ⇔\(\sqrt{(x-0)^{2}+(y-a)^{2}}=\sqrt{(x-x)^{2}+(y-(-a))^{2}}\)
両辺二乗して、
\(x^{2}+(y-a)^{2}=(y+a)^{2}\)
式を整理すると、
\(x^{2}+y^{2}-2ay+a^{2}=y^{2}+2ay+a^{2}\)
さらに移項して、\(x^{2}=4ay\)
この式が放物線の方程式(の一つ)です。
2種類の放物線のグラフと式
上の項で導いた通り、放物線には2種類の式があり、1つはy=4ax2 (これはこれまで学んできた2次関数の式とほぼ同じです)で、
もう1つは、y2=4axです。後者の式は、yが2乗されておりグラフも横倒しのような形になっているのが特徴です。(この場合の準線は、『x=-a』となります)
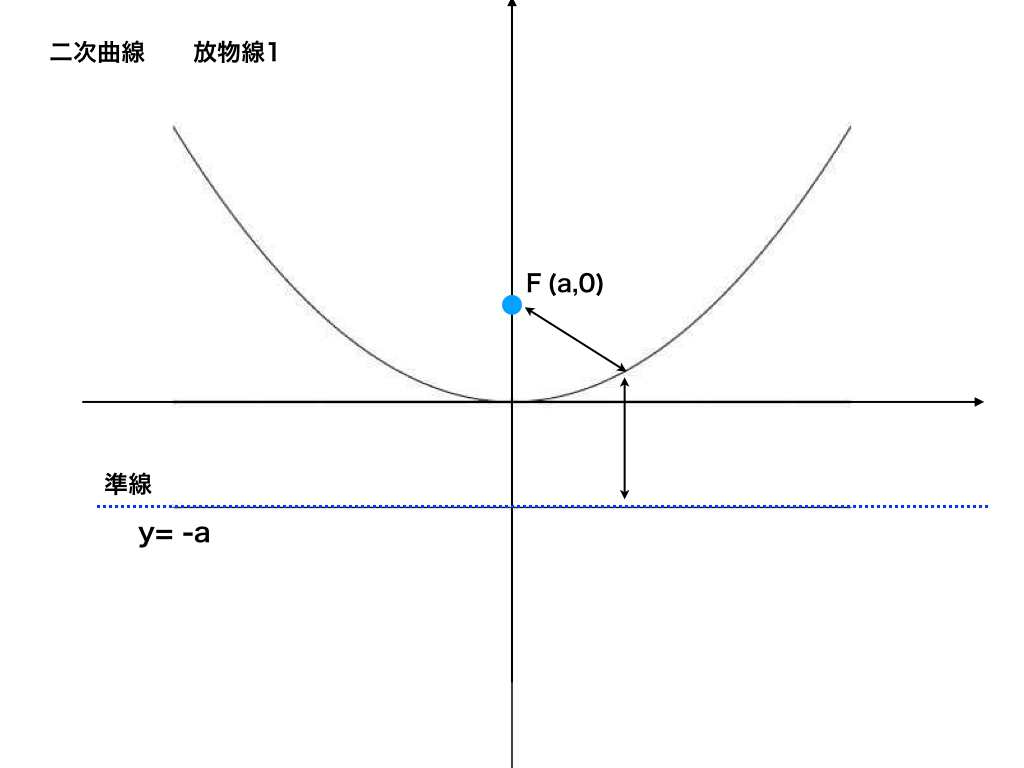
<\(x^{2}=4ay型の放物線\)>
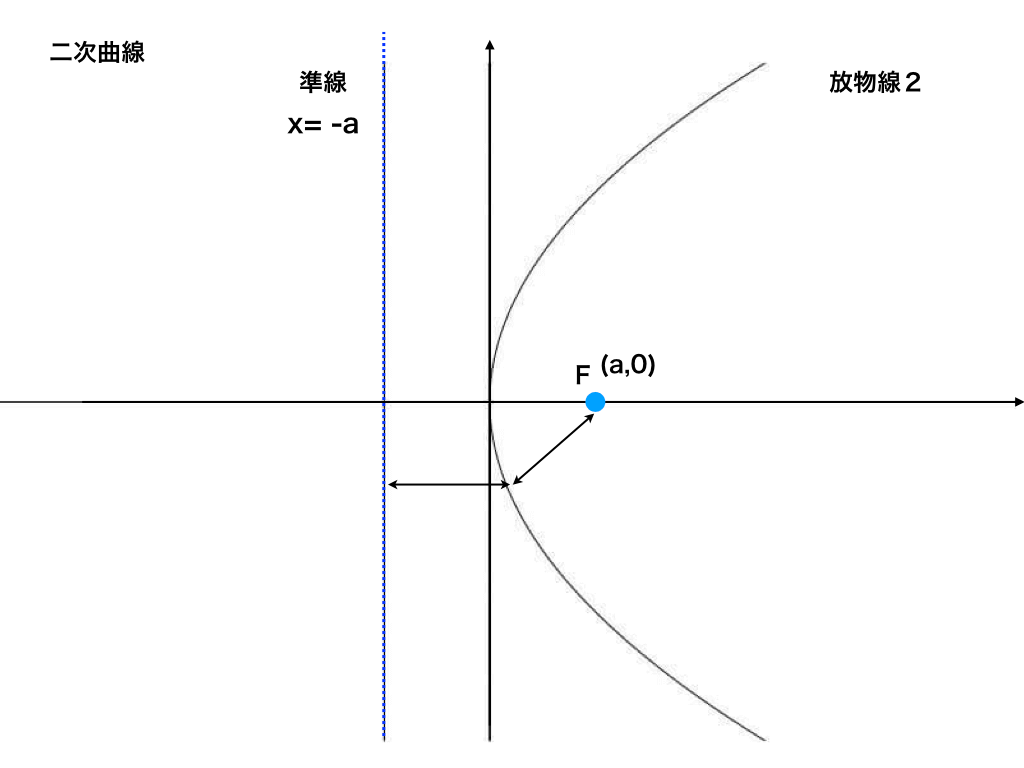
<\(y ^{2}=4ax型の放物線\)>
円錐曲線/放物線のまとめと次回「二次曲線第2回:双曲線へ」
・3種類の二次曲線の定義と式、焦点の座標などの特徴を類題を探して解きながら”自然と覚えている”状態にしましょう。(残りの楕円と双曲線は現在作成中です。)
・2つの円錐を上下にくっつけて切断した時の『切り方』によってその断面が変化するイメージを持っておきましょう。
・次回は二次曲線の第2回として、”双曲線”の式の導出法や、焦点・漸近線の求め方・それぞれの言葉の意味などを詳しく解説します。
二次曲線シリーズ関連記事
第1回:「二次曲線(円錐曲線)の概要と放物線」(今ここです)
第2回:「双曲線のグラフ・特徴と式の導出法」
第3回:「楕円の特徴・グラフと式の導出、面積公式など」
発展:「二次形式とその標準形」
最後までご覧いただき、有難うございました。
当サイトでは、読者の皆さんのご意見・記事のリクエスト等の募集を行なっています。
ご質問・ご意見がございましたら、是非コメント欄にお寄せください。
SNS等でB!やシェア、Twitterのフォローをしていただけると励みになります。
その他のお問い合わせ/ご依頼に関しましては、お問い合わせページからご連絡下さい。

