線形写像とは何か?ImやKer(像と核)についてもイラストで徹底解説!

線形写像をはじめから!

＜この記事の内容＞：線形代数における『線形写像』について、イラストを使いながら基本的な意味から『核（カーネル）・像（イメージ）』と言った理解しにくい事柄まで紹介しています。

＜これまでの記事＞：「０から学ぶ線形代数シリーズまとめページ」・「集合と写像（単射・全射・全単射）とは」

＜本記事で扱うそれぞれの項のさらに詳しい解説するための追加記事を作成中です＞

線形写像の意味・イメージ

まずは、『線形写像』というものの意味を見ていきましょう。

写像とは

写像は、『うつす』という言葉があるように、ある集合から別の集合へその『要素』を対応させることを言います。

もっとも身近な例を１つ挙げると、f(x)=3xという一次関数があります。

この式のxに１、２、３・・・と代入すると、f(x)は3、6、9・・・と対応した値を返します。ここで、xに入れる数を”要素”、要素が集まった(1,2,3・・・）のことを”集合”と名付けているのです。

そして、この数をf(x)（2,4,6・・・）へ対応させることを『写像』というのです。

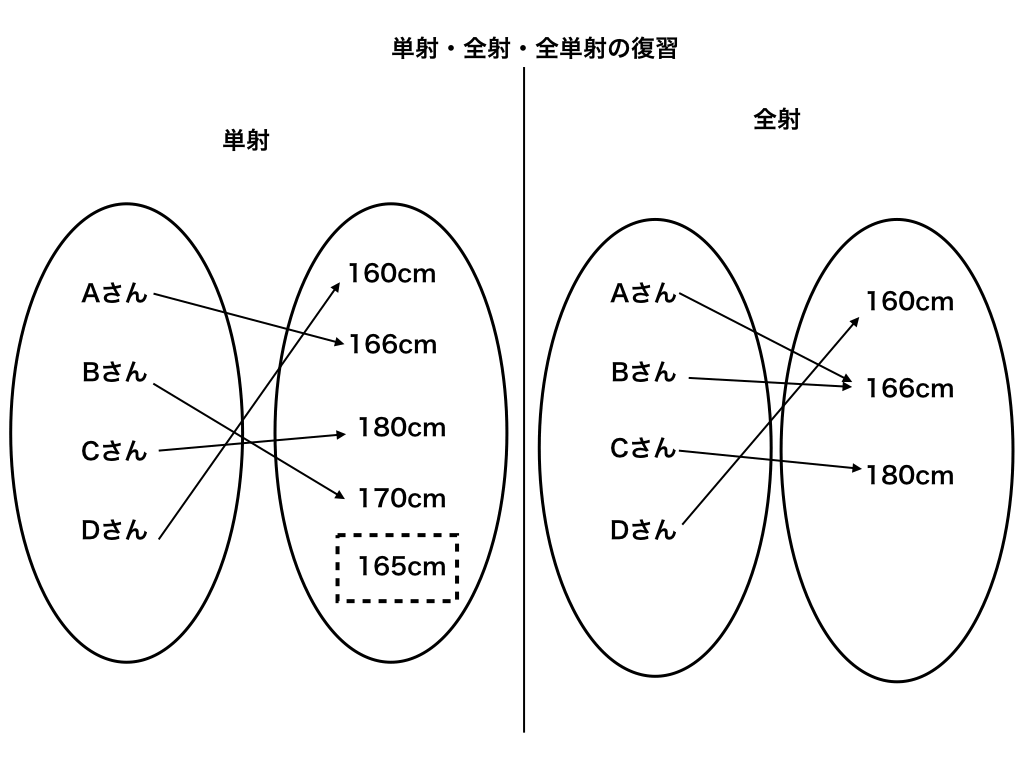
単射/全射/全単射の復習

また、写像には『単射・全射・全単射』があり、ここではその復習を簡単に行っておきます。

次にこの二つを合わせた全単射です。

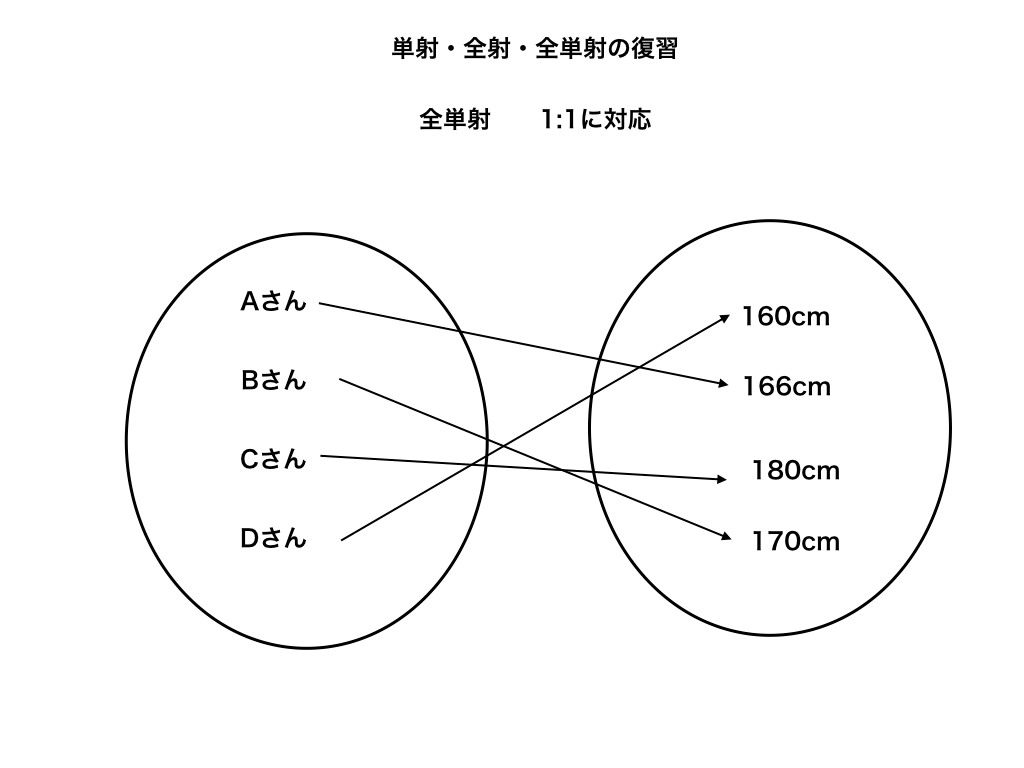
全単射

線形性を持つ写像＝線形写像

このような写像に、『線形性』を持ったものが『線形写像』です。

線形性とは：R上のベクトル空間V、V’があるとき、$$任意の\vec{x},\vec{y}\in V,k \in Rが、$$

$$f(\vec{x}+\vec{y})=f(\vec{x})+f(\vec{y})･･･(1)$$

$$f(k\vec{x})=kf(\vec{x})･･･(2)$$

ここでの"f"は"写像"を意味するので、Vの元x,yを”足してからV'へ写したもの”と、x,yを”別々に写したものを足し合わせても”同じになるということを(1)で定義しており、

(2)では、”k（実数）倍したVの元xをV'へ写したもの”と、xをV→V'へ”写してからk倍したもの”は同じであるということを言っています。

この(1),(2)を同時に満たす写像を『線形性を持つ』写像＝線形写像と呼びます。

表現行列

これまで、様々な使い方を紹介してきた『行列』ですが、線形写像においてはもとのベクトル空間の元（＝要素）に行列をかけることによって、V'に移る先を決めることができます。

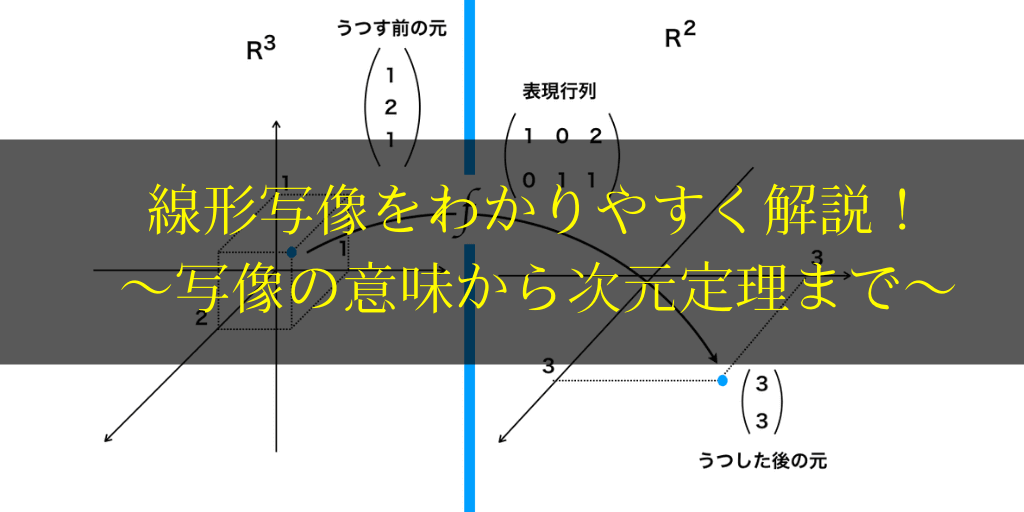
例えば、R³のベクトル空間V中の$$\begin{pmatrix}
1 \\
2 \\
1
\end{pmatrix}$$に行列$$P=\begin{pmatrix}
1 & 0 & 2 \\
0 & 1 & 1
\end{pmatrix}$$をかけることで、R²のベクトル空間V’の$$\begin{pmatrix}
3 \\
3
\end{pmatrix}$$へ写すことができます。

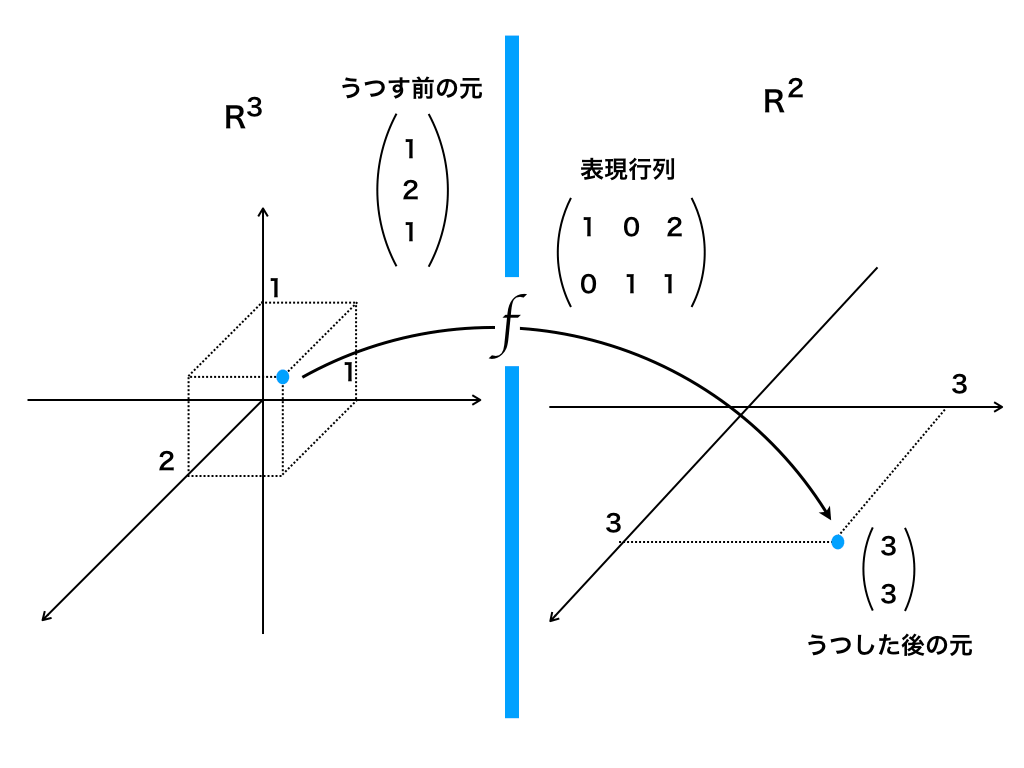
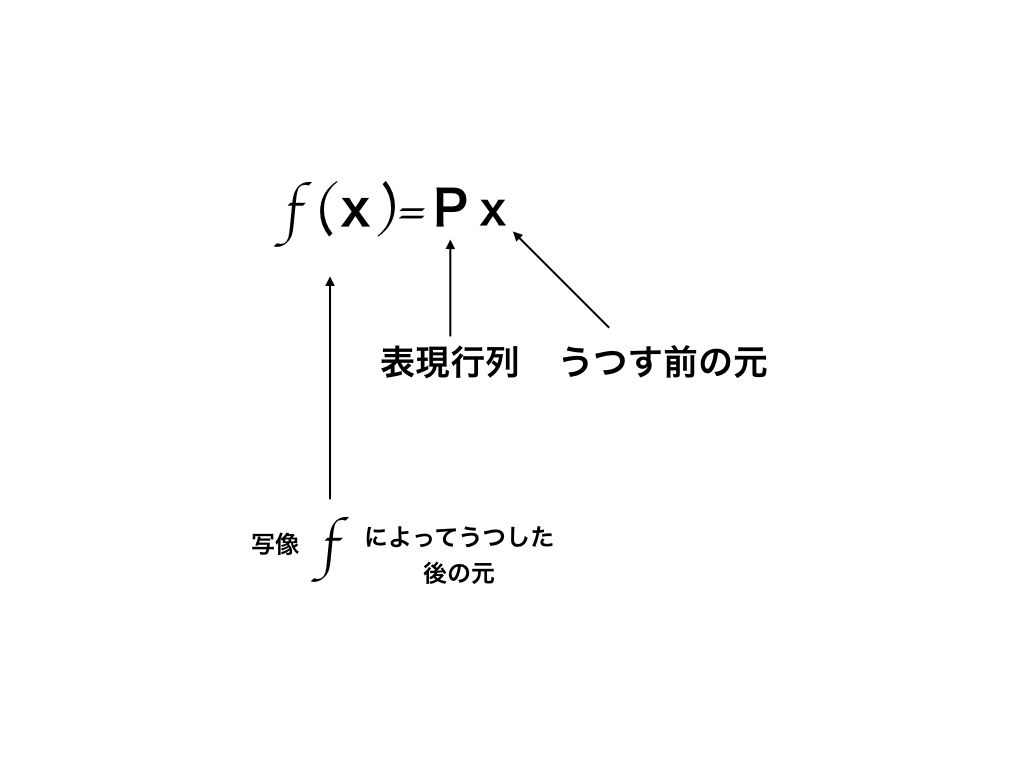
上の例のように、写像fによってうつされるxとうつされた後のf(x),そして表現行列には

$$f(\vec{x})=P\vec{x}$$の関係が成り立ちます。

線形変換

線形変換（一次変換）については『行列の一次変換って何？わかりやすく紹介』で解説していますが、ここでも簡単に紹介しておきます。

線形写像のうち、同じ次元（R^nからR^n）のベクトル空間からベクトル空間へとうつすもの（のことを『線形(一次)変換』と呼んでいます。

イメージfとカーネルf（Im f, Ker f)とは

線形写像の大体の意味を理解すると、次に出現するのがこの項で解説する『Im f』・『Ker f』です。

なんとなく難しそうに感じますが、解説図を見ながら１つ１つ意味を考えれば必ず理解できます。

Im fを図解

Im fと書いて（イメージ"f"）と呼び、このfは写像をあらわす"f"です。

今、以下の図のように線形空間VとV’があり、$$Vの任意の元\vec{x}$$を写像fでV'に写した『Vのfによる像』のことをIm fとします。

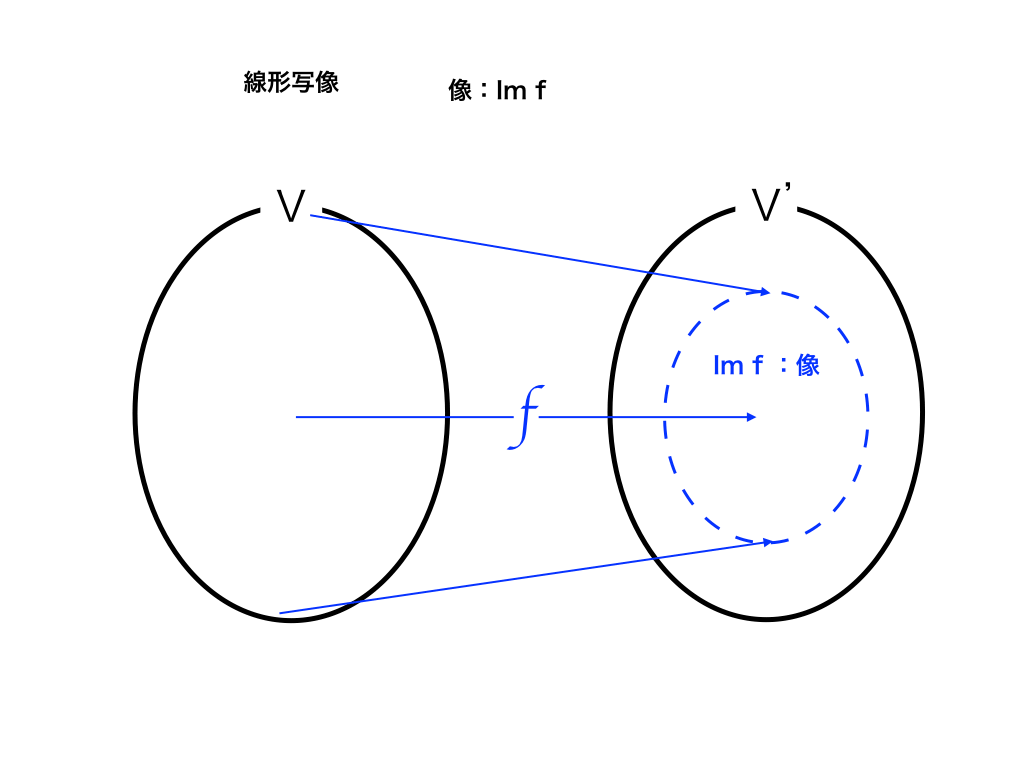
f:V→V'

$$Im f=f(V)=〔f(\vec{x})|x\in V〕$$はV'の部分空間となります。

Ker fを図解

線形写像を行うと、（線形空間：V→V’への写像fとします）以下の図のようにV'で『０ベクトルに”潰れてしまう”』Vの部分集合のことを”カーネル（核）”fと言います。

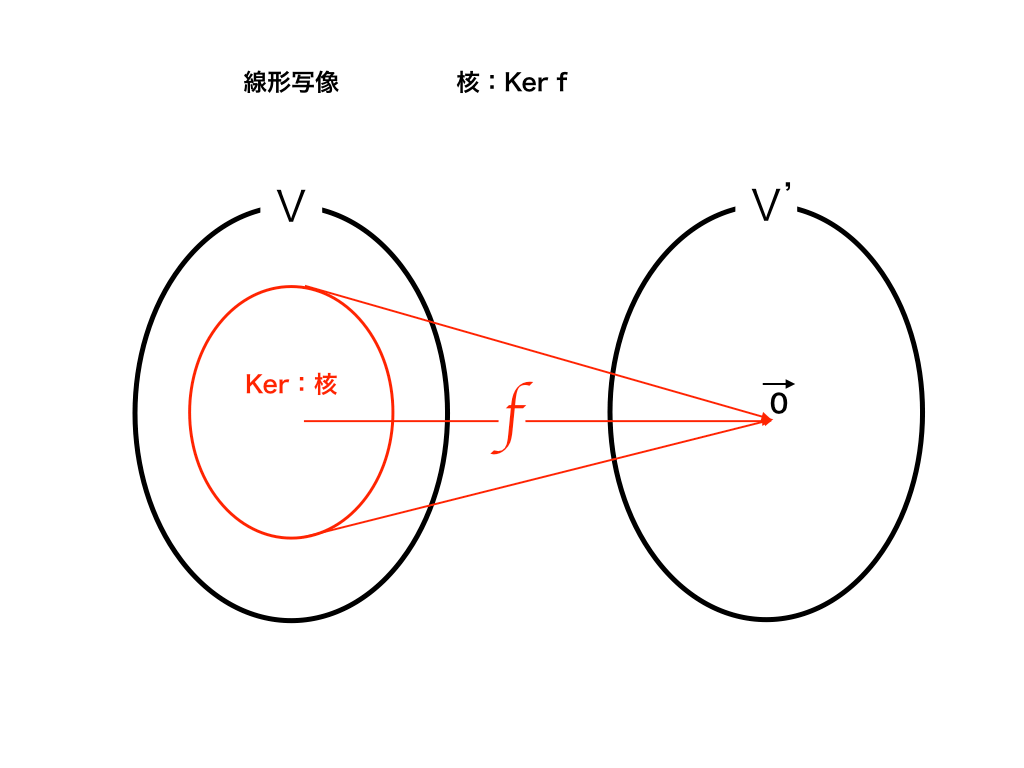
カーネルfの図

次元定理：(dim V)＝dim Ker f+dim Im f

詳しくは次回解説しますが、『次元定理』という定理によって、ベクトル空間Vの次元は、イメージfの次元とカーネルfの次元の和が成り立つことが知られています。

まとめと続編・線形代数の関連記事へ

・線形性を持ち、ベクトル（線形）空間からベクトル（線形）空間へ元をうつす＝『線形写像』

（以下、線形写像を行う前のベクトル空間をV→(f)→V’、写像fによってうつしたのちのベクトル空間をV'とすると）

・線形変換は、写像の中でも”うつす前”と”うつした後”の線形空間の次元が同じもの

・表現行列とは、線形空間のある元(xとする)を写した際(f)にただ一つ定まる行列(P)：f(x)=Px

・カーネルfは零ベクトルに『潰れてしまう』元の集合（Vの部分集合）

・イメージfは、写像を行なったときに、Vの元がどれだけV'に残っているかを示すV'の部分集合

線形代数のまとめと続編記事

高校数学のベクトルの知識０の状態から、学部２年レベルくらいまでの線形代数を学べる記事まとめです。

＞＞「線形代数を高校レベルから解説！記事総まとめ」＜＜

次回は、今回の内容をさらに深く掘り下げるほか、実際に図形を線形変換によって回転させたり拡大・縮小する方法などを詳しく扱います。

「（作成中）次元定理・様々な線形変換・etc,,,」

今回も最後までご覧いただきまして有難うございました。

「スマナビング！」では読者の皆さんのご意見や、記事のリクエストの募集を行なっています。ぜひコメント欄までお寄せください。

・いいね！や、B！、SNSなどでシェアをしていただけると励みになります！

その他のお問い合わせ・ご依頼に付きましては、お問い合わせページからご連絡下さい。